计算机组成原理定点运算

Posted 2021-10-16 mosun_zgs

定点运算

加减法运算

连同符号位一起相加，符号位产生的进位自然丢掉

• 加法
  • 整数： [A]补+[B]补=[A+B]补 (mod 2^(n+1))
  • 小数： [A]补+[B]补=[A+B]补 (mod 2)
• 减法 A-B=A+(-B)
  • 整数：[A-B]补=[A]补+[-B]补=[A+(-B)]补 (mod 2^(n+1))
  • 小数：[A-B]补=[A]补+[-B]补=[A+(-B)]补 (mod 2)
    

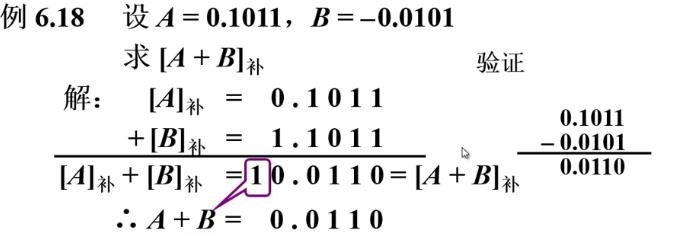
溢出判断

• 一位符号位判断溢出

  • 两个数符号相同，结果符号与操作数符号不同，即为溢出
  • 最高有效位的进位 ⊕ 符号位的进位=1
    • 如 1⊕0=1 0⊕1=1有溢出
    • 如 1⊕1=0 0⊕0=0没有溢出

• 两位符号位判断溢出

• 

乘法运算

人工计算乘法（原码一位）

• 乘积的符号心算求得
• 符号位单独处理
• 乘数的某一位决定是否加被乘数
• 位积一起相加
• 乘积的位数扩大一倍

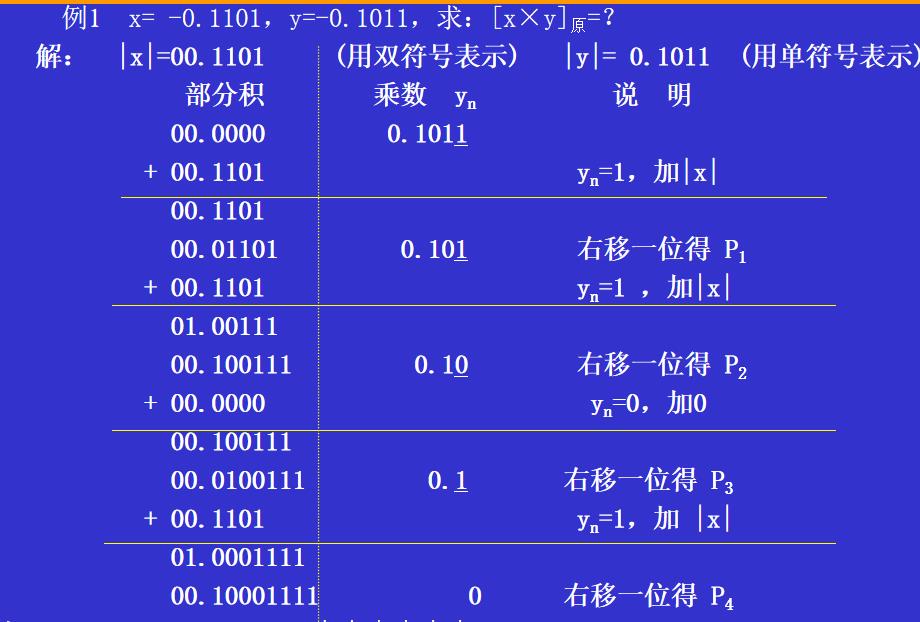
改进后竖式乘法过程

• 被乘数和乘数均取绝对值参加运算，符号位单独考虑。
• 被乘数取双符号，部分积的长度与被乘数的长度相同，初值为0。
• 从乘数的最低位的yn位开始对乘数进行判断，
  • 若yn=1，则部分积加上被乘数|x|，然后右移一位；
  • 若yn=0，则部分积加上0，然后右移一位。
• 重复判断n次。
  

乘法小结：

• 乘法运算可用加和移位实现
  • n=4时，加4次，移动4次
• 被乘数只与部分积的高位相加
• 硬件中，需要3个寄存器，一个保存被乘数，2个具有移位功能

除法

人工计算除法

• 商的符号单独处理
• 心算上商
• 余数不动低位补“0”
• 减右移一位的除数
• 上商位置不固定

人工计算除法与机器除法比较

人工计算	机器除法
商符单独处理	符号位异或形成
心算上商	/x/-/y/>0上商1，/x/-/y/<0上商0
余数不动低位补0，减右移一位的除数	余数左移一位，低位补0减除数

---

原码一位除法

• 设被除数[x]原＝xf，x１x２…xn
• 设除数[y] 原＝yf，y１y２…yn
• 商的符号： Qf= xf⊕yf
• 商的数值： |Q|=|x|/|y| （绝对值相除）
• 被除数不等于0，除数不能为0

恢复余数法

• 若余数为正数：

  • 上商1
  • 左移一位
  • 加上除数的绝对值的负数的补码

• 若余数为负数：

  • 上商0
  • 无需左移
  • 加上除数的绝对值的补码
  • 变成正数后，无需上商，但要左移，然后加上除数的绝对值的负数的补码；
  • 若还是负数的话，则反复操作以上步骤

不恢复余数法 （恢复余数法的改良，又称加减交替法）

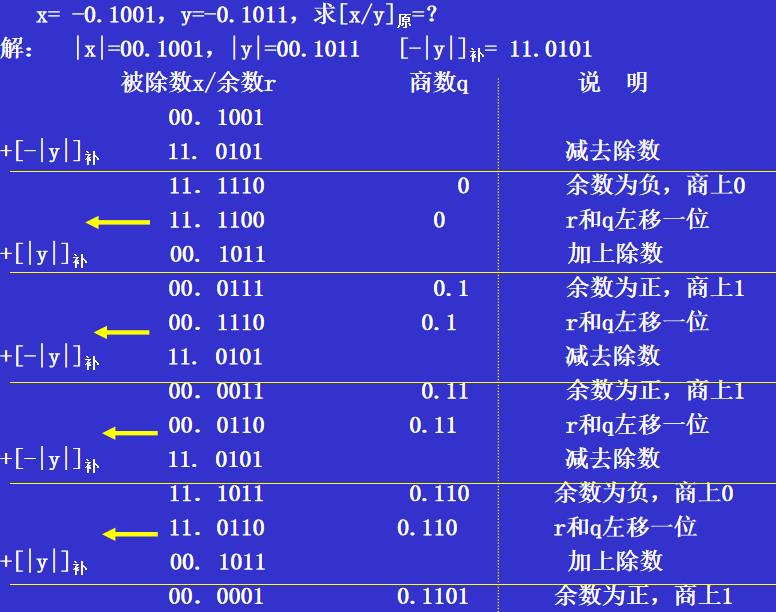
1. 符号位不参加运算，并要求|x|<|y|
2. 先用被除数减去除数
   • 当余数为正时，商上1，余数左移一位，再减去除数。
   • 当余数为负时，商上0，余数左移一位，再加上除数。
3. 当第n+1步余数为负时需加上 |y| 得到第n+1步正确的余数，最后余数为r^n×2(-n)(余数与被除数同号)。

特点

• 上商n+1次
• 第一次上商判断是否溢出
• 移动n次，加n+1次
• 用移位的次数判断出发是否结束

浮点数的加减运算

1. 对阶（原则：小阶向大阶看齐）

• 求阶差： 要对阶，首先应求出两数的阶码m和n之差，即
  ΔE＝m－n
  • 当m=n即，若ΔＥ＝0，则表示两数的阶码相等；若ΔＥ＞0，则表示m＞n；若ΔＥ＜0，则表示m＜n。
  • 当m≠n时，要通过尾数的移位以改变m或n，使之相等，在对阶时，总是使小阶向大阶看齐。
  • 若m＞n，则将操作数y的尾数右移一位，y的阶码n加1，直到m＝n为止。
  • 若m＜n，则将操作数x的尾数右移一位，x的阶码m加1，直到m＝n为止。

2. 尾数求和

使两个数的阶码相等后，就完成了小数点对准的工作，这时可以执行尾数相加操作。尾数相加与定点数的加、减法相同。

3. 结果规格化

• 规格化数：尾数的基值r =n, 1/n≤|S|＜1
• 规格化数判断：
• S>0 规格化形式：00.1××…×（真值原码补码反码 正数都一致）
• S<0 规格化形式：
  • 真值：-00.1××…×
  • 原码：1.1××…×
  • 补码：1.0××…×
  • 反码：1.0××…×
• 左规：尾数左移一位，阶码减1，直到数符和第一数位不同为止
• 右规（当尾数溢出(>1)时，需要右规，即01.××…或者10.×××…×时）：尾数右移一位，阶码加一

4. 舍入

在对阶和右规过程中，可能出现尾数末位移动造成丢失引起误差，则考虑舍入

• 0舍1入法（类似四舍五入）
• 末位恒置“1”法

5. 溢出判断

   运算结果的尾数部分符号位为01或10时，在定点加减法运算中表示溢出，而在浮点运算中并不表示溢出。在浮点数中，阶码的位数决定了数的表示范围，因此，浮点运算是在阶码的符号位出现01或10时，表示溢出，而尾数的符号位为01或10时，给出的是运算结果需要右规的信号。