有环链表，你的入口在哪？

Posted 2021-10-16 Rocky0429

大家好呀，我是 Rocky0429。

今天来切环形链表升级版，即除了判断一个链表是否是环形链表外，还要找到环形链表的入口在哪。

除了还是用到快慢指针外，加了一点数学思想。

不慌，保证安排的明明白白。

   LeetCode 142：环形链表 Ⅱ

题意

给定一个链表，返回链表开始入环的第一个节点。若链表无环，返回 null

示例

使用整数 pos 表示链表尾连接到链表中的位置(索引从 0 开始)。

输入：head = [3, 2, 0, -4]，pos = 1

输出：返回索引为 1 的链表节点。

解释：链表中有一个环，其尾部连接到第二个节点。

输入：head = [1]，pos = -1

输出：返回 null

解释：链表中没有环。

提示

pos 不作为参数进行传递，仅标识链表的实际情况。

0 <= 链表节点数 <= 10^4

10^-5 <= Node.val <= 10^5

pos 为 -1 或者链表中的一个有效索引。

题目解析

难度中等，题目解决分为两步走：

1. 判断是否有环。

2. 若有环，找入口，找到结束；若无环，结束。

第一步：判断是否有环。

做法同 LeetCode 141

判断是否有环，一般使用快慢指针。

快慢指针，顾名思义，是使用速度不同的指针（可用在链表、数组、序列等上面），来解决一些问题。

这些问题主要包括：

• 处理环上的问题，比如环形链表、环形数组等。

• 需要知道链表的长度或某个特别位置上的信息的时候。

快慢指针这种算法证明，它们肯定是会相遇的，快的指针一定会追上慢的指针，可以理解成操场上跑步，跑的快的人套圈跑的慢的人。

一般用 fast 定义快指针，用 slow 定义慢指针。

速度不同是指 fast 每次多走几步，slow 少走几步。一般设定的都是 fast 走 2 步，slow 走 1 步。

当然设置成别的整数也是可以的，比如 fast 走 3 步，slow 走 1 步。

第二步：找入口。

这一步要用到点儿数学，下面来看一张简图。

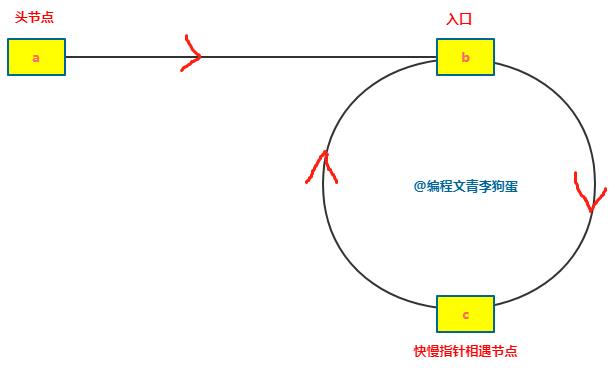
假设：

• 从头节点到入口的距离为 ab。

• 从入口到相遇点的距离为 bc。

• 从相遇点到入口的距离为 cb。

则链表环的长度 = bc + cb。

那么快慢指针相遇时所走过的步数为：

fast_step = ab + bc + n * (bc + cb) 【公式 1】

slow_step = ab + bc 【公式 2】

n 指的是 fast 指针走过的圈数，n 的取值肯定是 n ≥ 1，因为快指针 fast 最少要多跑一圈才能追上慢指针 slow。

又由于快指针每次走 2 步，慢指针每次走 1 步，所以又有：

fast_step = 2 * slow_step 【公式 3】

综合公式 1、公式 2、公式 3，得出：

ab + bc + n * (bc + cb) = 2 * (ab + bc) 【公式 4】

整理得：

ab = (n - 1) * (bc + cb) + cb 【公式 5】

其中 (n - 1) * (bc + cb) 正好是 (n - 1) 个环形的长度。

为了更好的理解公式 5，我们假设 n = 1，也就是快指针 fast 指针走一圈就可以碰到慢指针 slow。

那么公式 5 变成：

ab = cb

你看这个公式好巧妙，ab 是从节点到入口的距离，cb 是从相遇节点到入口的距离，这说明什么呢？

说明同时从头节点和相遇节点出发的两个指针，每次走 1 步，最终会在入口处相遇。

所以如果判断链表是环形链表，“找入口”就成了，在找到快慢指针相遇节点时，设置两个新节点 flag1 和 flag2。

其中 flag1 指向头节点，flag2 指向快慢指针相遇节点，然后每次移动 1 步，直至 flag1 和 flag2 相遇。

图解

以 head = [3, 2, 0, -4]，pos = 1 为例。

第一步：判断是否有环

第 1 步：初始化快慢指针。每次 slow 走 1 步，fast 走 2 步。

第 2 步：slow 移动 1 步，fast 移动 2 步。

第 3 步：同上。

第 4 步：同上。

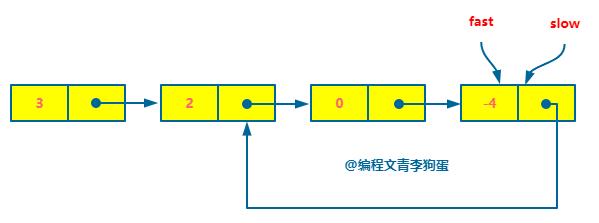
此时 fast = slow，判断有环。

第二步：找入口。

第 1 步：设置两个新节点，flag1 指向头节点，flag2 指向快慢指针相遇节点。

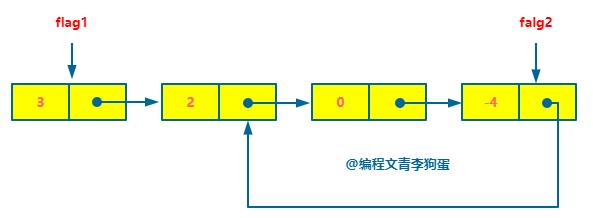
第 2 步：flag1 移动 1 步，flag2 移动 1 步。

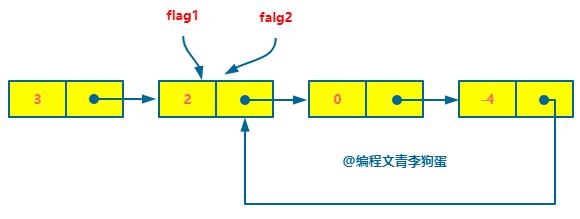
此时 flag1 和 flag2 相遇，找到入口索引为 1，返回索引为 1 的链表节点。

判断是否有环的时间复杂度是 O(n)，找入口的时间复杂度也是 O(n)，所以总的时间复杂度 = O(n) + O(n) =  O(n)。

因为只使用了 fast、slow、flag1 和 flag2 四个指针，所以空间复杂度为 O(1)。

代码实现

Python 代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None


class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:


        # 空链表或链表只有一个节点，无环
        if not head or head.next == None:
            return None


        # 初始化快慢指针
        fast = slow = head


        # 如果不存在环，肯定 fast 先指向 null
        # 细节：fast 每次走 2 步，所以要确定 fast 和 fast.next 不为空，不然会报执行出错。
        while fast and fast.next:


            # 快指针移动 2 步，慢指针移动 1 步
            fast = fast.next.next
            slow = slow.next


            # 快慢指针相遇，有环
            # 然后开始找入口
            if fast == slow:


                # 初始化 flag1 和 flag2
                flag1 = head
                flag2 = fast


                # 找 flag1 与 flag2 相遇的节点
                while flag1 != flag2:
                    flag1 = flag1.next
                    flag2 = flag2.next
                return flag1


        return None

Java 代码实现

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {// 有环
                ListNode index1 = fast;
                ListNode index2 = head;
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}

图解有环链表入口到这就结束啦，这算是我们第一次碰到稍微有点难度的题。

没慌吧？

其实也就这么回事，一步步的跟着本蛋走下来，什么都能解决！

加油，别忘了我的么么哒呀。

我是 Rocky0429，我们下次见！