算法：N皇后问题51. N-Queens

Posted 2021-10-15 架构师易筋

51. N-Queens

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space, respectively.

Example 1:

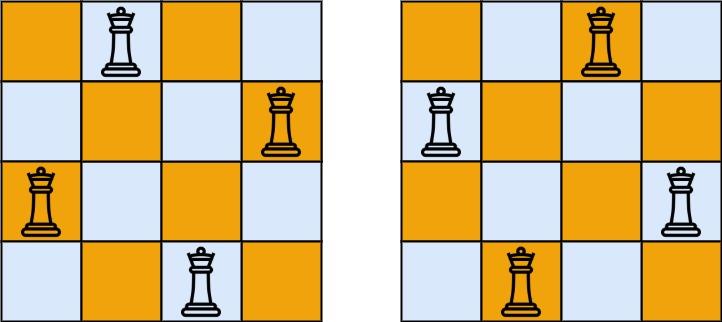
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

Constraints:

1 <= n <= 9

深度优先回溯解法

下面的推导出Queen可以互相攻击的公式

1. 行相同x == row
2. 列相同y == col
3. 左对角线相同x - y = row - col
4. 右对角线相同x + y = row + col
   
   用树形结构调用，形象化recursive回溯调用路径
   

The reason it checks (x + j == y + i || x + y == i + j || x == i):

Every time we find a existing ‘Q’, 3 conditions need to be met before we can place a new ‘Q’ in the new column:

1. no confict in columns : self explanatory as we put ‘Q’ col by col.
2. no confict in rows : x == i
3. no conflict in diagonals : Math.abs(x-i) == Math.abs(y-j)
   For Math.abs(x-i) == Math.abs(y-j),

if x > i, y > j , x - i = y - j => x + j = y + i
if x < i, y < j, i - x = j - y => x + j = y + i
if x > i, y < j, x - i = j - y => x + y = i + j
if x < i, y > j, i - x = y - j => x + y = i + j

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> list = new ArrayList<>();
        char[][] board = new char[n][n];
        for (int x = 0; x < n; x++)
            for (int y = 0; y < n; y++) 
                board[x][y] = '.';
        dfs(list, board, n, 0);
        return list;
    }
    
    private void dfs(List<List<String>> list, char[][] board, int n, int colIndex) {
        if (colIndex == n) {
            addResult(list, board);
            return;
        }
        for (int row = 0; row < n; row++) {
            if (validate(board, n, row, colIndex)) {
                board[row][colIndex] = 'Q';
                dfs(list, board, n, colIndex + 1);
                board[row][colIndex] = '.';
            }
        }
    }
    
    private void addResult(List<List<String>> list, char[][] board) {
        List<String> rowList = new ArrayList<>();
        for (char[] rows: board)
            rowList.add(new String(rows));
        list.add(rowList);
    }
    
    private boolean validate(char[][] board, int n, int x, int y) {
        for (int r = 0; r < n; r++) {
            for (int c = 0; c < n; c++) {
                if (board[r][c] == 'Q' && (x == r || y == c || x + c == y + r || x + y == r + c)) {
                    return false;
                }
            }
        }
        
        return true;
    }
}

效率更高，更好理解的算法

上个算法要6ms，对上面的进行两个部分优化，可以降低到2ms

1. validate 的方法只要验证，小于当前位置的列、左斜对角、右斜对角即可；因为上一层已经是校验过的，所以就不用再次校验；
2. dfs校验row的维度更好理解；
   

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> list = new ArrayList<>();
        char[][] board = new char[n][n];
        for (int x = 0; x < n; x++)
            for (int y = 0; y < n; y++)
                board[x][y] = '.';
        dfs(list, board, n, 0);
        
        return list;
    }
    
    private void dfs(List<List<String>> list, char[][] board, int n, int row) {
        // terminate
        if (row == n) {
            // todo 1:
            addResult(list, board);
            return;
        }
        for (int col = 0; col < n; col++) {
            // todo 2:
            if (validate(board, n, row, col)) {
                // update status
                board[row][col] = 'Q';
                // drill down
                dfs(list, board, n, row + 1);
                // reset status
                board[row][col] = '.';
            }
        }
    }
    
    private void addResult(List<List<String>> list, char[][] board) {
        List<String> itemList = new ArrayList<>();
        for (char[] item: board) {
            itemList.add(new String(item));
        }
        list.add(itemList);
    }
    
    private boolean validate(char[][] board, int n, int row, int col) {
        for (int x = 1; x <= row; x++) {
            int currentX = row - x;
            if (board[currentX][col] == 'Q') return false;
            int leftDiagonal = col - x;
            if (leftDiagonal >= 0 && board[currentX][leftDiagonal] == 'Q') return false;
            int rightDiagonal = col + x;
            if (rightDiagonal < n && board[currentX][rightDiagonal] == 'Q') return false;
        }
        
        return true;
    }
}

参考

https://leetcode.com/problems/n-queens/discuss/19805/My-easy-understanding-Java-Solution
This video by tushar roy explains the validate function well:
https://youtu.be/xouin83ebxE?t=92