最长回文子串问题-Manacher算法建议收藏

Posted 2021-10-15 飞人01_01

前面我们讲过一个关于字符串的算法：KMP算法。今天我们来讲另外一个字符串算法：Manacher算法。这个算法是用于解决一个问题叫：最长回文子串。

前期文章：KMP算法

牛客网OJ链接

说的简单一点，给定一个字符串，返回的值是这个字符串的最长回文子串的长度。顾名思义，即是回文串，也是子串。

文章目录

• 一、BF算法
• 二、Manacher算法

一、BF算法

那上图的示例2为例：abc1234321ab。

最简单的思路就是从左到右遍历每一个字符。每来到一个字符位置，我们可以向左右两边进行扩展，分别比较左右两边的字符。如果相等，就继续向两边扩展；如果不相等，就停止，计算以当前字符，向两边扩展出的长度，就是以当前字符为中心的回文子串。比如：

就像上图这样，从左往右依次遍历即可。

上面这种思路确实能够解题，但是还有一个很重要的点，那就是假设给定的字符串是偶数个字符，那么这种方式就会错过一些回文子串的匹配，因为此时对于偶数个字符来说，对称点是在中间两个字符之间的，如下图：

所以以每个字符为中心点，向两边扩展，还是存在着一定的问题。如何解决呢？

那就是将原字符串进行处理，加工为一个含有特殊字符的字符串，比如原字符串为：123321,；加工后的字符串为：#1#2#3#3#2#1#；

也就是说，在每个字符的中间，加入其它字符，这样就能使一个偶数个字符的字符串，转换为奇数个字符的字符串。这样就可以遍历，向两边扩展了。

问题：我们所加入的字符，必须是原字符中没有的字符吗？

这个问题留作大家思考。

public static int getLengthOfSubString(String str) {
    if (str == null) {
        return 0;
    }

    char[] generateStr = generateString(str);
    int length = generateStr.length;
    int max = 0; //答案
    
    for (int i = 0; i < length; i++) {
        int tmp = 1; //每个字符都能以自己本身的字符作为回文子串。所以初始值是1
        int radius = 1; //回文半径，也就是以i位置为中心，半径radius的范围内

        while (i - radius >= 0 && i + radius < length) { //左右两边都在数组的范围内，循环继续
            if (generateStr[i - radius] == generateStr[i + radius]) {
                tmp += 2; //左右两个字符相等的情况
                radius++; //回文半径加1
            } else {
                break;
            }
        }

        max = Math.max(max, tmp); //判断当前的tmp是否是最长的回文子串
    }
    return max / 2; //因为我们比较的处理后的字符串，计算出的回文串要除以2.才是最终的答案
}

public static char[] generateString(String str) {
    char[] res = new char[str.length() * 2 + 1]; //原2倍长度，再加1
    int index = 0;
    for (int i = 0; i < res.length; i++) {
        //奇数位置放#，偶数位置放原字符
        res[i] = (i % 2) == 1? str.charAt(index++) : '#';
    }
    return res;
}

以上代码就是BF算法，暴力解。每个字符都需要遍历一次，而每次字符都需要向外扩展，最坏情况下，就是向外扩展一直到整个字符串结束。比如：1111111； 这种情况就是每个字符向外扩展，都会扩展很长，甚至是扩展至字符串结束，所以这个BF算法的时间复杂度是O(N²) 。

二、Manacher算法

Manacher算法也是在BF算法的基础之上，做了优化。所以大家看Manacher算法之前，先理解BF暴力解的流程。

Manacher算法引入了三个概念：

• 当前回文子串的中心点 ：C
• 当前已经遍历到最长回文子串的最右边界下标：R
• 回文半径数组；（用于存储已经扩展完成的回文子串的半径）

通过上面三个变量，我们就能解决这一难题了。话不多说，讲述推导过程。整体分为两个大步骤。C和R的初始值都是-1，也就是数组最左边的外面。

1. 当i位置（当前遍历的字符）不在R（最右边界）内时：

   

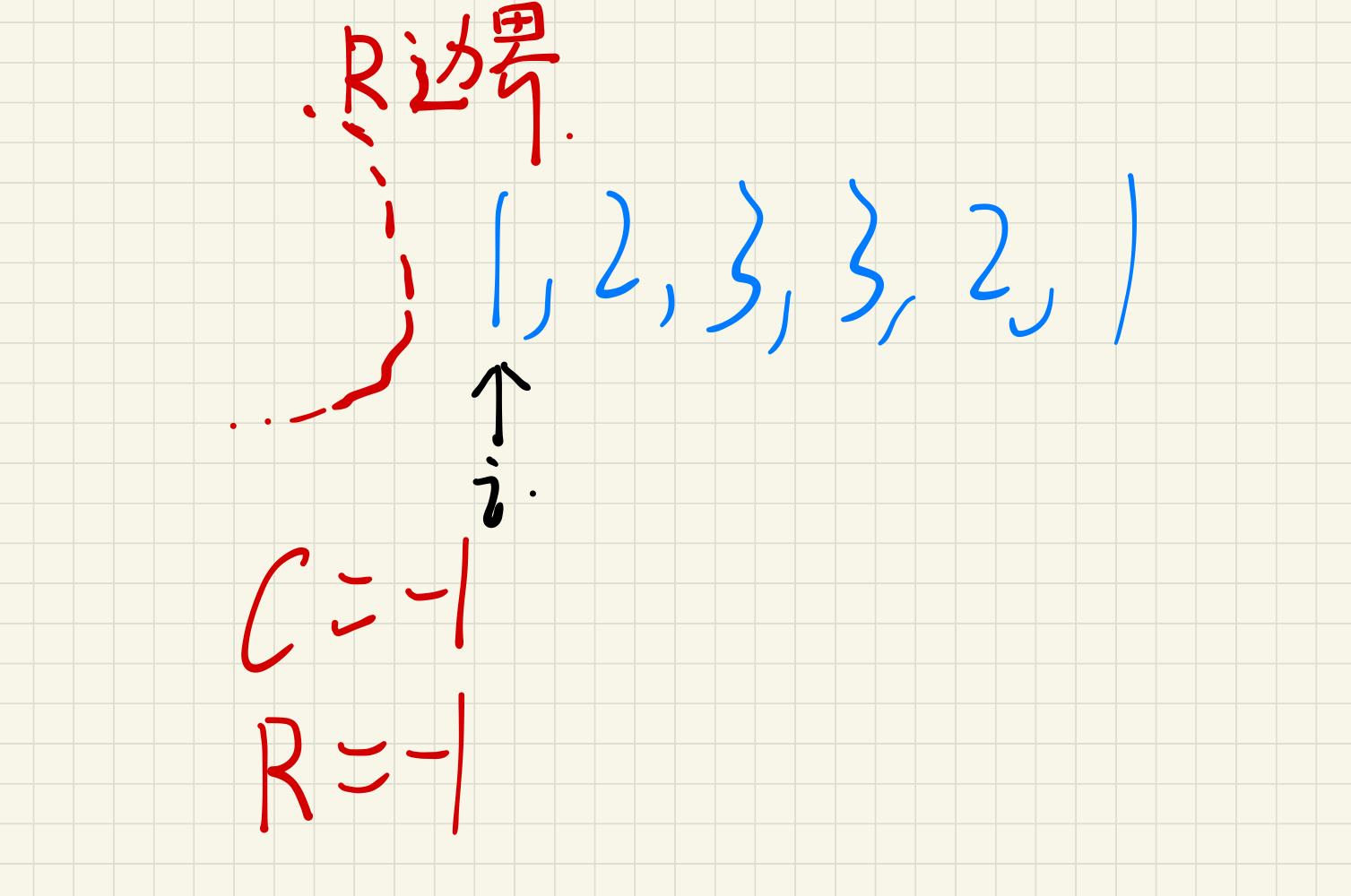
   此时这种情况，我们只能向左右两边进行扩展。这个没办法。重要的是第2种情况。

2. 当i位置（当前遍历的字符）在R（最右边界）内时：

   

   以7为中心，向两边扩展出来的回文子串，就是橙色括号圈起来的范围。此时的i就是在R边界的里面。

   当我们以中心点为对称点，做出i的对称点，如下图：

   

   做出来的对称点，我们就能得到这个点的下标。然后去回文半径数组里查这个下标对应的回文半径，就能得到关于这个对称点的回文子串。例如上图中黑色虚线框中的值。

   对于黑色虚线框的值，我们又可以分为三种小情况：

   • 黑色虚线框与以C中心点扩展的回文子串压线：

     压线的情况，就是上图中这种情况，黑色虚线框的左边界与橙色线重合。 根据对称性，因为黑色虚线框的值是回文子串，那么右边以i为中心，也能扩展出回文子串。如下图所示：

     

     所以我们可以直接通过对称点i得到已经完成匹配的回文子串。然后我们可以直接从i位置的已经计算好的回文子串外开始扩展。比如：左边值7和右边值1做比较，如果相等，当前回文半径加1，然后继续比较下一对字符。

   • 黑色虚线框的左边界，超过了以C中心点扩展的回文子串的左边界（超出）：如下图：

     

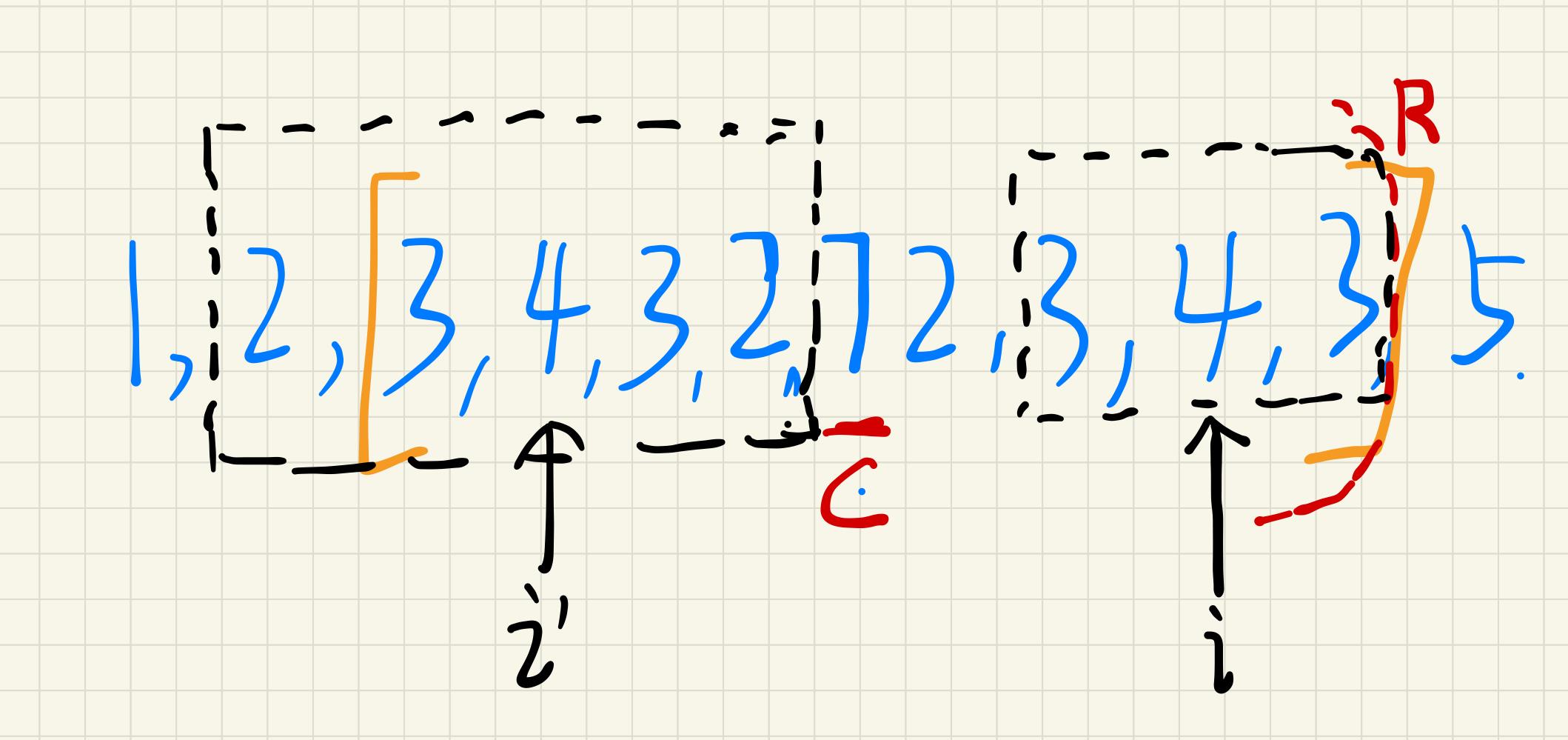
     对称点i，以它为中心对应的回文子串正如左边的黑色虚线框所示：2,3,4,3,2。此时虚线框已经超出了橙色线的范围，又因为橙色线范围内是一个回文子串。所以我们可以推导出当前i位置，至少有回文子串，就是（R-i）为半径的范围。即上图右边黑色虚线框内。

     此时我们只需要在此基础之上，比较R右边的值5 和 黑色虚线框左边的2，看是否相等。若相等，则再次比较下一对字符。依次类推。

   • 黑色虚线框整体，都是在以C中心点扩展的回文子串的左半部分（即没压线，也没超出）：如下图：

     

     此时以i位置为中心，向左右两边扩展，就可以从黑色虚线框两边开始比较字符了。

   上面三种情况，都是由对称点i得到关于该点的回文子串；再对称到右边i位置，以此为基础，继续向外扩展比较字符。那可能有同学就会疑惑，为什么就能从左边对称点i，就能推导出右边i位置的回文子串呢？ 证明如下：

   

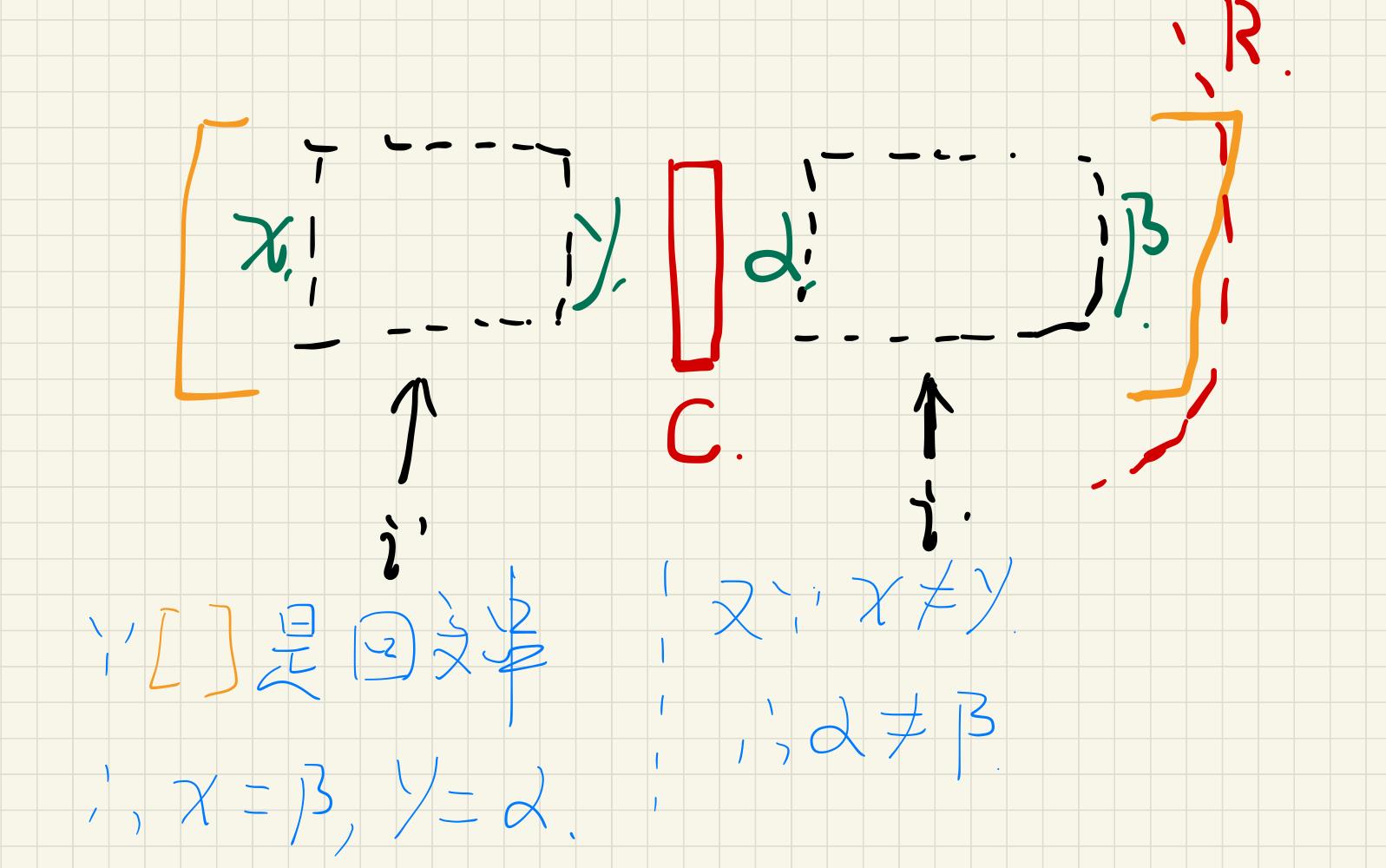
上述所有，就是Manacher的推导过程，就是通过对称，拿到C点左边的对称点。就能从回文半径数组中拿到该位置的回文子串。因此就能对应到C点右边的回文子串，在此基础之上进行字符比较，节省了一些已经比较过的字符的时间。

public static int manacherStr(String str) {
    if (str == null || str.length() < 1) {
        return 0;
    }

    char[] s = generateString(str);
    int length = s.length;
    int C = -1; //回文子串的中心点
    int R = -1; //最长回文子串的右边界
    int[] pArr = new int[length]; //回文半径数组
    int max = 0; //答案
    for (int i = 0; i < length; i++) {
        //判断i是否在R的范围内。如果不在，选择相应的对称点。
        pArr[i] = i < R? Math.min(R - i, pArr[2 * C - i]) : 1; 

        //以下循环，就是上面上面分析的3种小情况。也可以自己用if else语句
        while (i - pArr[i] >= 0 && i + pArr[i] < length) {
            if (s[i - pArr[i]] == s[i + pArr[i]]) { //左右两边的字符
                pArr[i]++; //回文半径加1
            } else {
                break;
            }
        }

        //更新 新的回文子串的右边界和 C中心点
        if (i + pArr[i] > R) {
            R = i + pArr[i];
            C = i;
        }
        max = Math.max(max, pArr[i]); //判断是否是最长回文半径
    }

    return max - 1; //最终的答案，与max的值，相差1
}

public static char[] generateString(String str) {
    char[] res = new char[str.length() * 2 + 1]; //原2倍长度，再加1
    int index = 0;
    for (int i = 0; i < res.length; i++) {
        //奇数位置放#，偶数位置放原字符
        res[i] = (i % 2) == 1? str.charAt(index++) : '#';
    }
    return res;
}

上述所有，就是Manacher算法的全部。Manacher就是在BF算法基础之上，新加了回文半径数组。对于这个数组来，可以解决很多关于字符串的问题，所以很好的掌握这个算法，对以后刷题有很大的帮助。

好啦，本期更新就到此结束啦！！！我们下期见！！！