❤️[数据结构]动图+万字详解栈和队列(动图+实例)建议收藏❤️
Posted Linux猿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了❤️[数据结构]动图+万字详解栈和队列(动图+实例)建议收藏❤️相关的知识,希望对你有一定的参考价值。
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,C/C++、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏:C/C++面试通关集锦 (优质好文持续更新中……)🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录
在日常的学习以及求职面试中,栈和队列是一块非常重要的内容,经常被提及,本篇文章总结了栈和队列基本概念及常用操作,并且分别使用数组和链表实现了栈和队列,简单易懂,想不会都难!赶紧来看下吧!
一、栈
1.1 什么是栈
栈是一种抽象数据结构,也是一种线性数据结构,具有后进先出(LIFO,Last In First Out)的特性,即:后进入栈中的元素在先进入元素的上面,故后进入栈中的元素先出栈,当然也可以说是先进后出,即:先进入的元素后出栈,一样的原理,只是说法不同。如下图所示:
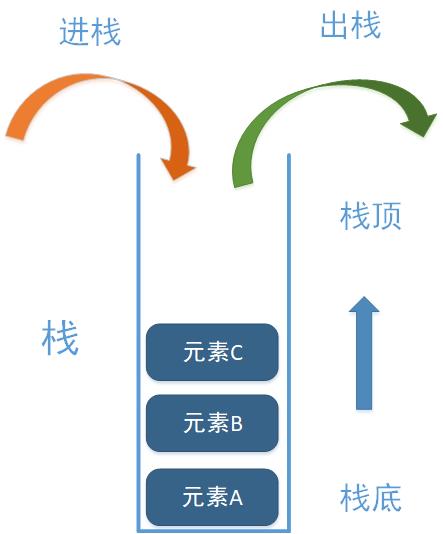
从上图可以看到,栈只有一个口,即是入口也是出口,后进入栈的元素 C,比先进入栈的 B 和 A 先出栈,这就是所谓的后进先出。如上图所示,栈有栈顶和栈底。
来看一下动图,如下所示:

1.2 实现方式
栈的实现可以通过数组或链表来实现,如下图所示:
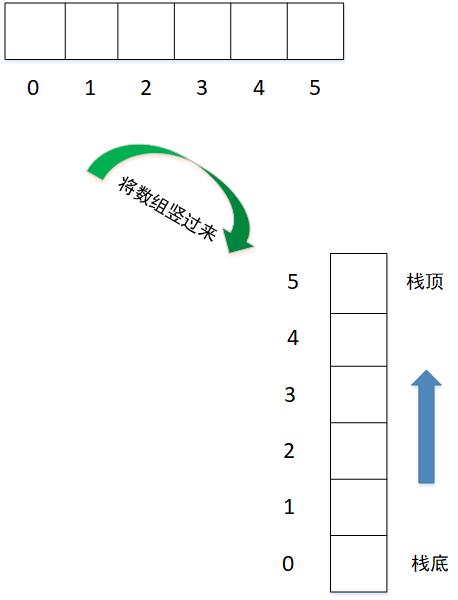
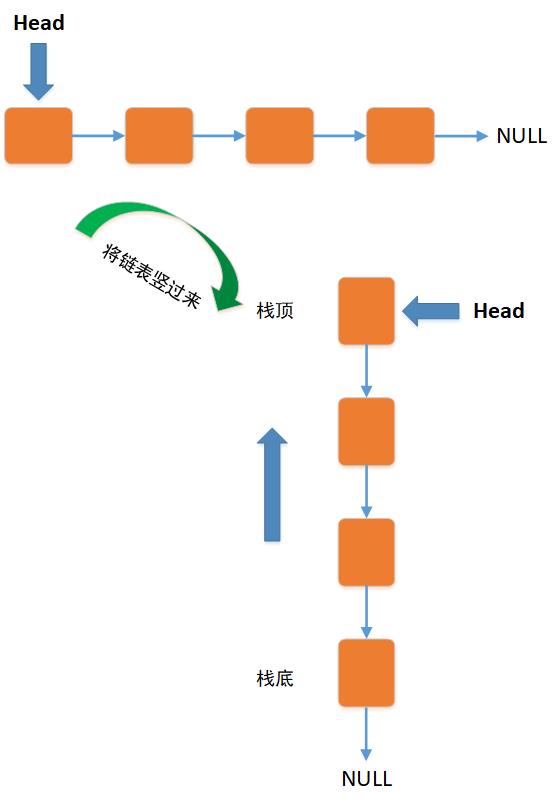
下面分别来看一下数组和链表来实现栈。
1.3 数组实现栈
1.3.0 类封装
下面用类封装了栈的常用操作,如下所示:
#define NUM 100000 // 栈的大小
class Stack {
int data[NUM]; // 数组模拟栈
int num; // 栈指针,指向栈顶元素
public:
Stack() { // 初始化
num = -1;
memset(data, 0, sizeof(data));
}
void push(int val); // 添加元素
int pop(); // 删除栈顶元素
int top(); // 返回栈顶元素
bool empty(); // 判断是否为空
int size(); // 栈大小
};上面是以 int 为例子,更好的封装是使用 C++ 的模板,这里为了便于理解采用了更简单的方式。
另一方面,数组还可以改成动态分配的形式,即:先分配一个初始数组,如果栈溢出了,则重新分配,将原先的内容拷贝到新分配的数组中,分配的方式可以参考 STL 的递增策略。
1.3.1 push 操作
向栈中添加元素,如下所示:
void Stack::push(int val) {
if(num >= NUM) {
cout<<"Stack Overflow!"<<endl;
return;
}
data[++num] = val;
}如上所示,先判断栈是否已满,未满则添加元素。可以将上面的 if 语句里的内容修改为增加栈容量。
1.3.2 pop 操作
删除栈顶元素,因为栈是后进先出的,如下所示:
int Stack::pop() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return data[num--];
}如上所示,先判断栈是否为空,不空则删除栈顶元素,只要栈顶指针移动即可。
1.3.3 empty 操作
判断栈是否为空,空返回 true,否则返回 false ,如下所示:
bool Stack::empty() {
return num == -1;
}这里也许有人会说“为啥不用 int 类型,返回 0 和 1 呢? 用 true 和 false 更好是因为 bool 类型占一个字节,而 int 通常占 4 个字节。
1.3.4 top 操作
返回栈顶元素,如下所示:
int Stack::top() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return data[num];
}先判断栈是否为空,如果非空则返回栈顶元素。
注意:这里不是删除,仅仅是返回栈顶元素的值。
1.3.5 size 操作
返回栈大小,如下所示:
int Stack::size() {
return num + 1;
}栈指针 num 是从 0 开始的,故返回 num+1。
1.3.6 数组栈测试
下面是测试上面的数组栈实现,如下所示:
int main()
{
Stack st;
st.push(10);
st.push(20);
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"The stack empty is "<<st.empty()<<endl;
cout<<"----------------------------------------"<<endl;
st.pop();
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"----------------------------------------"<<endl;
return 0;
}输出为:
The size of stack is 2
The top of stack is 20
The stack empty is 0
----------------------------------------
The size of stack is 1
The top of stack is 10
----------------------------------------1.4 链表实现栈
1.4.0 类封装
使用类封装栈,如下所示:
struct node { // 链表单个节点
int val; // 存储栈元素值
struct node* next;// 指向下一个元素的指针
node(int value) { // 赋初值
val = value;
}
};
class Stack {
struct node *index; // 指向栈顶元素
int s_size; // 记录栈容量
public:
Stack() { // 初始化
index = nullptr;
s_size = 0;
}
~Stack() ;
void push(int val); // 添加元素
int pop(); // 删除栈顶元素
int top(); // 返回栈顶元素
bool empty(); // 判断是否为空
int size(); // 栈大小
};struce node 是链表中的单个元素, class Stack 包含栈的各种操作,这里使用 s_size 记录栈的容量,便于操作。当然,这里是以 int 为例,可以将其修改为 C++ 的模板形式。
1.4.1 push 操作
向栈中添加元素,如下所示:
void Stack::push(int val) {
struct node* tmp = new node(val);
if(tmp == nullptr) {
cout<<"Failed to allocate space!"<<endl;
return;
}
tmp->next = index;
index = tmp;
s_size++;
}如上所示,这里不用判断栈是否已满,需要判断一个是否分配成功。
1.4.2 pop 操作
删除栈顶元素,因为栈是后进先出的,如下所示:
int Stack::pop() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
int tmpVal = index->val; // 暂存栈顶元素
index = index->next; // 删除栈顶元素
s_size--; // 栈元素个数减一
return tmpVal; // 这个返回下栈顶元素
}如上所示,先判断栈是否为空,不空则删除栈顶元素,只要栈顶指针移动即可。
1.4.3 empty 操作
判断栈是否为空,空返回 true,否则返回 false ,如下所示:
bool Stack::empty() {
return index == nullptr;
}1.4.4 top 操作
返回栈顶元素,如下所示:
int Stack::top() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return index->val; // 仅仅返回栈顶元素
}因为 index 一直指向栈顶元素,所以直接返回 index->val。
1.4.5 size 操作
返回栈大小,如下所示:
int Stack::size() {
return s_size;
}这里使用 s_size 记录栈大小,不然每次都要遍历链表。
1.4.6 链表栈测试
下面是测试上面的链表栈实现,如下所示:
int main()
{
Stack st;
st.push(10);
st.push(20);
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"The stack empty is "<<st.empty()<<endl;
cout<<"----------------------------------------"<<endl;
st.pop();
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"----------------------------------------"<<endl;
return 0;
}
输出为:
linuxy@linuxy:~/Stack$ g++ -o main Stack.cpp
linuxy@linuxy:~/Stack$ ./main
The size of stack is 2
The top of stack is 20
The stack empty is 0
----------------------------------------
The size of stack is 1
The top of stack is 10
----------------------------------------
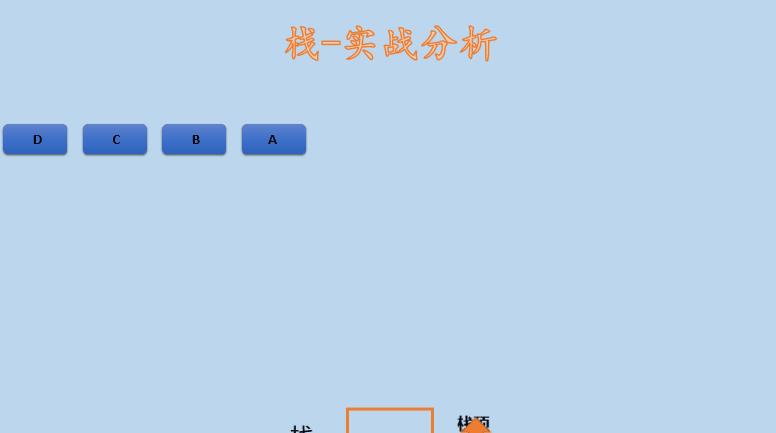
linuxy@linuxy:~/Stack$ 1.5 实战分析
模拟元素栈操作,如何实现从下面的入栈顺序到出栈顺序。
入栈顺序:A B C D
出栈顺序:C B D A
如上所示,需要找到一种方法,实现从入站次序到出站次序,这是栈经常考的题目,步骤如下:
(1)因为第一个出站的是 C,所以 A,B ,C依次入栈;
(2)这时,C 在栈顶,C 出栈;
(3)因为第二个出栈的是 B,当前栈顶为 B,所以直接让 B 出栈;
(4)B 出栈后,当前栈顶为 A,但是,应该是 D 出栈,所以先让 D 进栈;
(5)当前栈顶为 D,下一个出栈元素为 D,让 D 出栈;
(6)当前栈顶元素为 A,下一个出栈元素对应 A,所以 A 出栈;
下面来看下动图:
1.6 复杂度分析
1.6.1 时间复杂度
不管是链表实现的栈,还是数组实现的栈,push 和 pop 操作的时间复杂度都是O(1)的,链表实现的栈中 clear 操作是O(n)的,因为需要释放所有的链表空间,其它操作都是O(1)的。
1.6.2 空间复杂度
链表相对于数组更节省空间,因为链表使用到才会分配,数组是提前分配好,而且如果栈满时,数组还需要重新分配。
1.7 栈的应用
(1)深度优先搜索
深度优先搜索的非递归实现通常使用栈作为辅助的数组结构。
(2)软件中的回退和前进功能
(3)拓扑排序
二、队列
2.1 什么是队列
队列是一种线性结构的抽象数据类型,可以实现先进先出(FIFO,First In,First Out),即:先进入的元素,先出队列,可以比喻为日常排队买东西。
如下图所示:
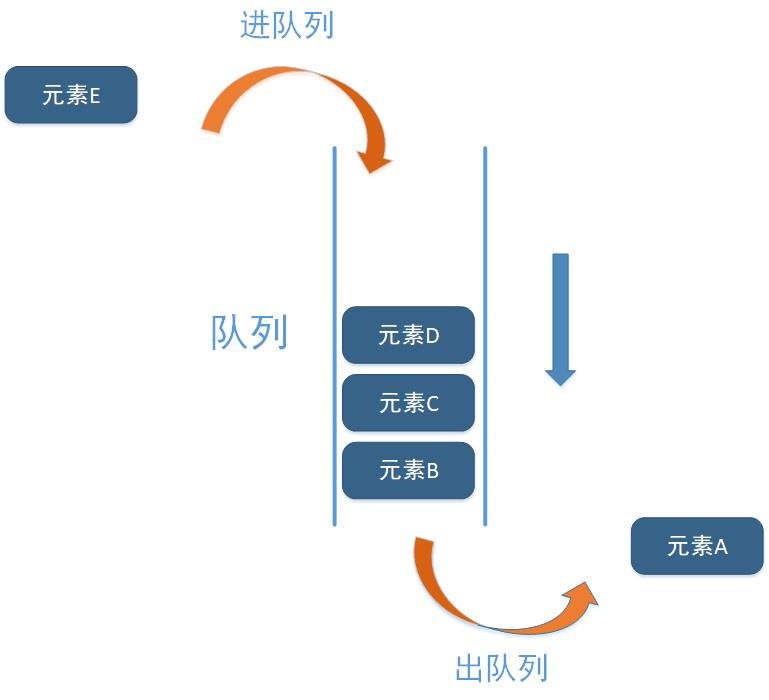
从上图可以看到,队列和栈不同,队列有两个口,而且是一个只允许进入元素,一个只允许出元素,后进入栈的元素C,比先进入栈的 B 和 A 先出栈,这就是所谓的后进先出。如上图所示,栈有栈顶和栈底。
来看一下动图,如下所示:

2.2 实现方式
队列的实现可以通过数组或链表来实现,如下图所示:
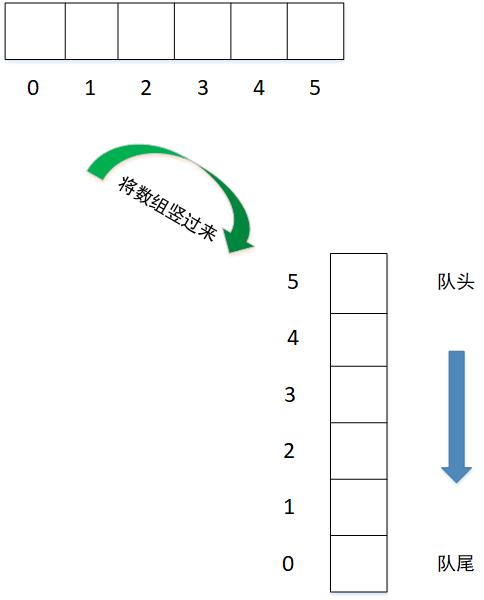
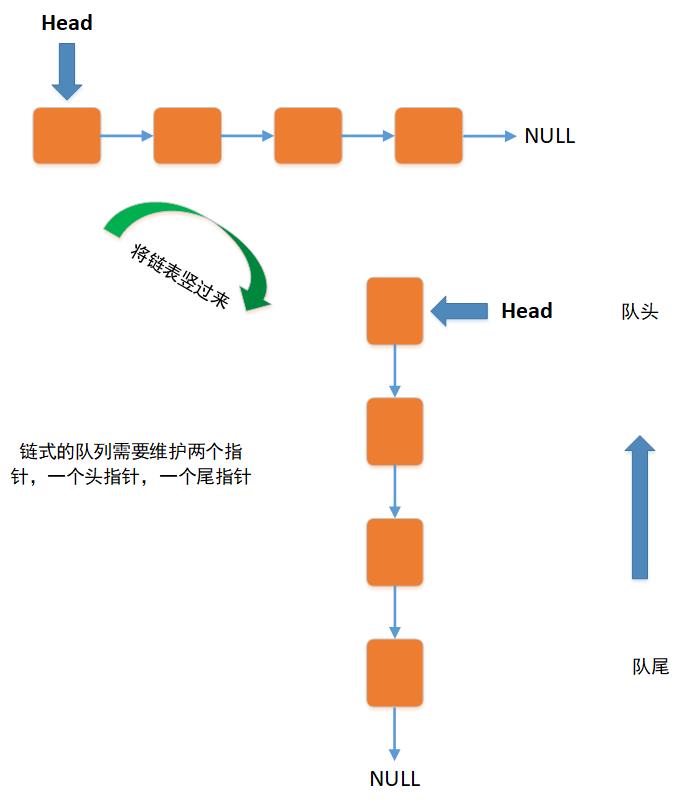
2.3 数组实现队列
2.3.0 类封装
下面是使用类封装了队列,如下所示:
#define NUM 100000 // 队列大小
class Queue {
int data[NUM]; // 数组模拟队列
int first; // 头指针,指向队列顶部
int last; // 尾指针,指向队列尾部
public:
Queue() { // 初始化
first = 0;
last = 0;
memset(data, 0, sizeof(data));
}
void push(int val); // 添加元素
int pop(); // 删除队列头元素
int front(); // 返回队列头元素
bool empty(); // 判断是否为空
int size(); // 队列大小
int back(); // 返回队列尾元素
};data 存储队列数据,first 和 last 分别指向队列头部和尾部。
2.3.1 push 操作
向队列中添加元素,如下所示:
void Queue::push(int val) {
if(last >= NUM) {
cout<<"Queue Overflow!"<<endl;
return;
}
data[last++] = val;
}先判断队列是否已满,未满则添加元素,添加元素只需要移动尾指针即可。
2.3.2 pop 操作
删除队列头元素,如下所示:
int Queue::pop() {
if(empty()) {
cout<<"Queue Empty!"<<endl;
return -1;
}
return data[first++];
}如上所示,先判断队列是否为空,不空则删除队列头元素,只需要头指针 first 移动即可。
2.3.3 front 操作
返回头元素的值,和栈的 top 操作相同的原理,如下所示:
int Queue::front() {
if(empty()) {
cout<<"Queue Empty!"<<endl;
return -1;
}
return data[first];
}先判断队列是否为空,非空则返回头元素。
2.3.4 empty 操作
判断队列是否为空,如下所示:
bool Queue::empty() {
return first == last;
}直接比较 first 与 last 是否相等即可。
2.3.5 size 操作
判断队列元素个数,如下所示:
int Queue::size() {
return last - first;
}使用队列尾指针与头指针之前的举例便是元素个数。
2.3.6 back 操作
返回队列尾元素,如下所示:
int Queue::back() {
if(empty()) {
cout<<"Queue Empty!"<<endl;
return -1;
}
return data[last-1];
}先判断是否为空,不为空则返回 last - 1 所在的元素,因为 last 指向尾元素的下一个位置。
2.3.7 数组队列测试
下面是对上面数组实现的队列的测试,如下所示:
int main()
{
Queue que;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"----------------------------------------"<<endl;
que.push(10);
que.push(20);
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The front of queue is "<<que.front()<<endl;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"----------------------------------------"<<endl;
que.pop();
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The front of queue is "<<que.front()<<endl;
return 0;
}输出为:
linuxy@linuxy:~/Stack$ ./main
The queue empty is 1
The size of queue is 0
----------------------------------------
The size of queue is 2
The front of queue is 10
The queue empty is 0
----------------------------------------
The size of queue is 1
The front of queue is 20
linuxy@linuxy:~/Stack$2.4 链表实现队列
2.4.0 类封装
struct node { // 链表节点
int val; // 链表值
struct node* next;
node(int value) {
val = value;
}
};
class Queue {
struct node *first; // 指向队列头元素
struct node *rear; // 指向队列尾元素
int s_size; // 记录队列元素个数
public:
Queue() { // 初始化
first = nullptr;
rear = nullptr;
s_size = 0;
}
~Queue();
void push(int val); // 添加元素
int pop(); // 删除队列头元素
int front(); // 返回队列头元素
bool empty(); // 判断是否为空
int size(); // 队列元素个数
void back(); // 返回队列尾元素
};first 指向队列头元素,rear 指向队列尾元素,s_size 记录队列中的元素个数。
2.4.1 push 操作
向队列中添加元素,添加到队列尾部,因为队列是先进先出,如下所示:
void Queue::push(int val) {
struct node* tmp = new node(val);
if(tmp == nullptr) {
cout<<"Failed to allocate space!"<<endl;
return;
}
if(rear == nullptr) { // 添加第一个元素
first = tmp;
rear = tmp;
tmp->next = nullptr;
} else { // 已有元素
rear->next = tmp;
tmp->next = nullptr;
rear = tmp;
}
s_size++;
}这里需要先分配空间,第一次添加元素需要将 first 和 rear 都指向该元素,否则添加到尾部即可,别忘记增加 s_size。
2.4.2 pop 操作
删除队列头元素,如下所示:
int Queue::pop() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
struct node* tmp = first;
first = first->next;
int val = tmp->val;
delete tmp;
s_size--;
return val;
}先判断队列是否为空,不为空则移动队列头指针,别忘记释放空间。
2.4.3 front 操作
返回队列头元素的值,并不是删除哦!如下所示:
int Queue::front() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return first->val;
}队列的 front 和 栈的 top 原理类似。
2.4.4 empty 操作
判断队列是否为空,如下所示:
bool Queue::empty() {
return first == nullptr;
}2.4.5 size 操作
判断队列元素个数,如下所示:
int Queue::size() {
return s_size;
}这里使用了一个辅助变量 s_size,不然每次求队列元素个数都需要遍历一次链表。
2.4.6 链表队列测试
下面是测试上面的链表队列的实现,如下所示:
int main()
{
Queue que;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"----------------------------------------"<<endl;
que.push(10);
que.push(20);
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The top of queue is "<<que.front()<<endl;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"----------------------------------------"<<endl;
que.pop();
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The top of queue is "<<que.front()<<endl;
cout<<"----------------------------------------"<<endl;
return 0;
}输出结果为:
linuxy@linuxy:~/Queue$ ./main
The queue empty is 1
The size of queue is 0
----------------------------------------
The size of queue is 2
The top of queue is 10
The queue empty is 0
----------------------------------------
The size of queue is 1
The top of queue is 20
----------------------------------------
linuxy@linuxy:~/Queue$2.5 实战分析
采用层次遍历的方法遍历如下二叉树:
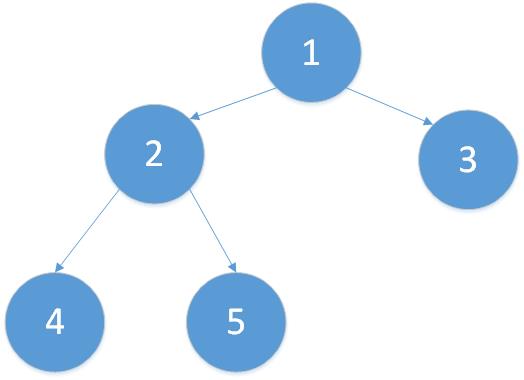
层次遍历上图的二叉树,即:从上到下一层一层的遍历二叉树的节点,按照这个思路,遍历步骤为:
(1)先访问 1 节点,1节点有两个孩子节点,1 节点出队列后,将 2 和 3 两个节点入队;
(2)访问 2 节点,2 节点出队,2 节点有两个子节点 4 和 5,2 节点出队后,4 和 5 节点入队;
(3)访问 3 节点,3 节点没有子节点,直接出队;
(4)依次访问 4 和 5 节点,这两个节点都没有子节点,所以出队即可。
(5)所有节点按照层次遍历的方式访问完毕!
来看一下动图:

2.6 复杂度分析
2.6.1 时间复杂度
不管是链表实现的队列,还是数组实现的队列,push、pop、empty、front 等操作的时间复杂度都是O(1)的。
2.6.2 空间复杂度
链表相对于数组更节省空间,因为链表使用到才会分配,数组是提前分配好,而且如果队列满时,数组还需要重新分配。
2.7 队列的应用
(1)广度优先搜索
广度优先搜索的实现通常使用队列作为辅助的数组结构。
(2)在一些资源请求或任务调度中,往往是先来先处理。
三、总结
栈和队列都有很强的特性,栈是后进先出,队列是先进先出,应用在不同的应用场景中。
欢迎关注下方👇👇👇公众号👇👇👇,获取更多优质内容🤞(比心)!
以上是关于❤️[数据结构]动图+万字详解栈和队列(动图+实例)建议收藏❤️的主要内容,如果未能解决你的问题,请参考以下文章