《糊涂算法》之八大排序——计数排序

Posted 2021-10-15 一条coding

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《糊涂算法》之八大排序——计数排序相关的知识，希望对你有一定的参考价值。

📚 八大排序算法合集——两万字，8张动图，450行代码。大厂面试必备。

🌲 配套源码地址：《八大排序》源码，提取码：5ehp

哈喽，大家好，我是一条~

今天给大家带来《糊涂算法》专栏的第二期内容——排序算法的讲解。相信无论是初学者学习还是大厂面试，都少不了排序算法这关，即使没学过算法，对冒泡排序也不会陌生。

今天，一条就带大家彻底跨过「排序算法」这道坎，保姆级教程建议收藏。⭐️

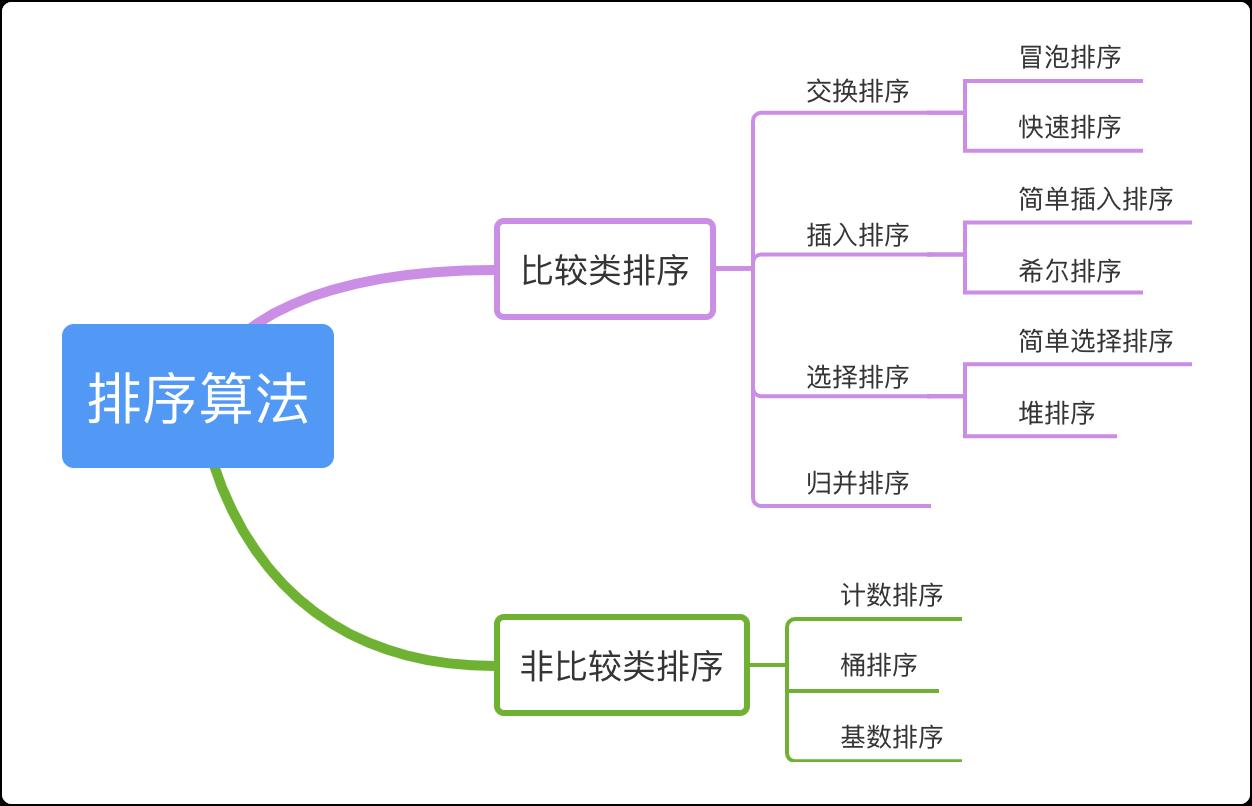
准备

古语云：“兵马未动，粮草先行”。想跟着一条一块把「排序算法」弄明白的,建议先准备好以下代码模板。

📢 观看本教程需知道基本循环语法、两数交换、双指针等前置知识。

📚 建议先看完代码和逐步分析后再尝试自己写。

新建一个Java工程,本文全篇也基于Java语言实现代码。
建立如下目录结构

在MainTest测试类中编写测试模板。

/**
 * 测试类
 * Author：一条
 * Date：2021/09/23
 */
public class MainTest {
    public static void main(String[] args) {
        //待排序序列
        int[] array={6,10,4,5,2,8};
        //调用不同排序算法
				// BubbleSort.sort(array);

        // 创建有100000个随机数据的数组
        int[] costArray=new int[100000];
        for (int i = 0; i < 100000; i++) {
            // 生成一个[0,100000) 的一个数
            costArray[i] = (int) (Math.random() * 100000);
        }

        Date start = new Date();
        //过长，先注释掉逐步打印
				//BubbleSort.sort(costArray);
        Date end = new Date();
        System.out.println("耗时："+(end.getTime()-start.getTime())/1000+"s");
    }
}

该段代码内容主要有两个功能：

调用不同的排序算法进行测试
测试不同排序算法将10w个数排好序需要的时间。更加具象的理解时间复杂度的不同

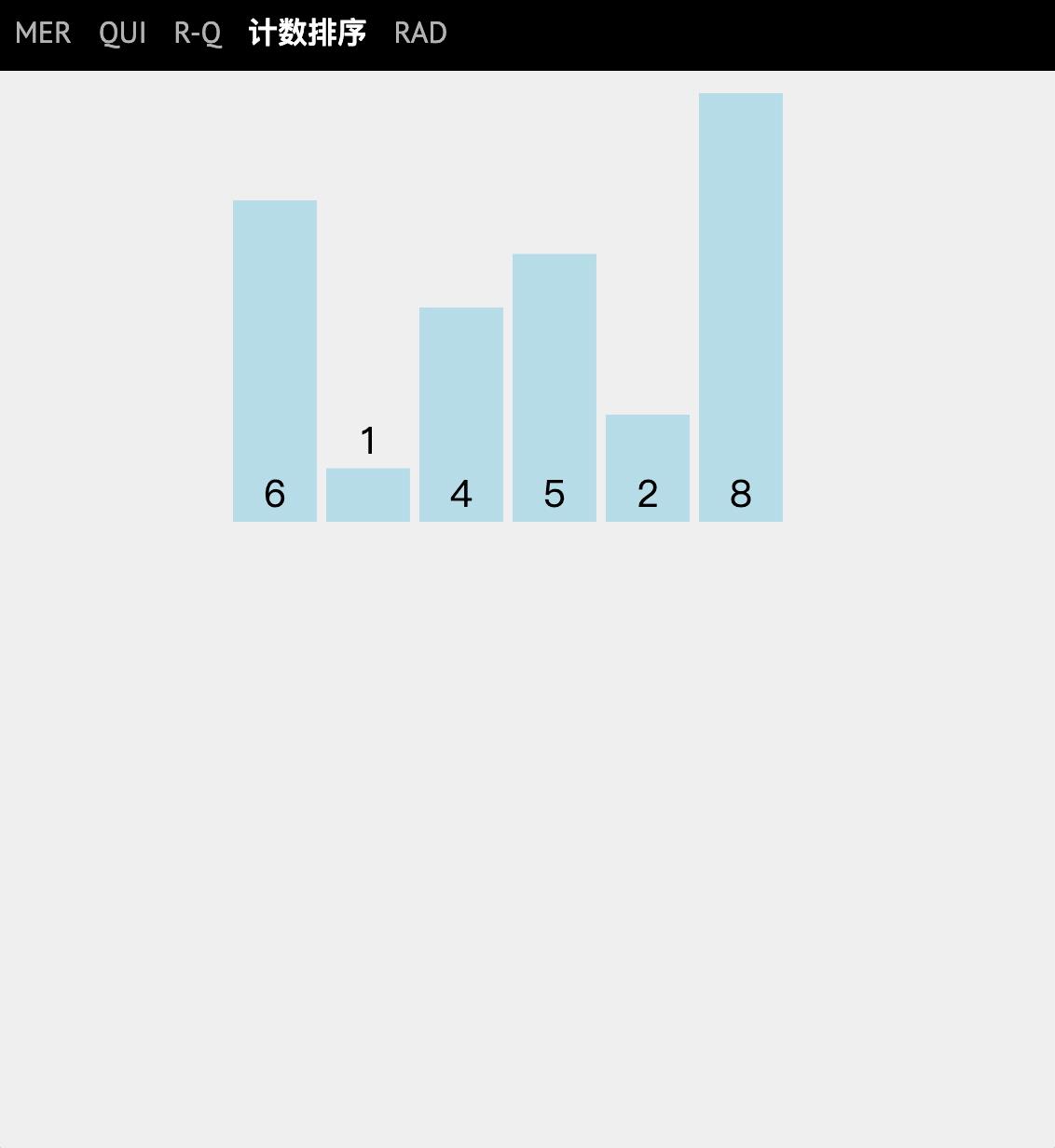
计数排序

从这里开始都是非比较排序。

基本思想

假如输入一个数x，如果我们可以找到比该数小的数有几个，那么就可以直接将x放入到对应的输出数组的位置。
比如测试序列中的x=5，，比5小的有2个，那么毫无疑问5就该排在第三位。

动图讲解

代码实现

public class CountSort {
    public static void sort(int[] array) {
        System.out.println("计数排序开始--------");
        //计算最大值和最小值，用于确定count[]的长度
        int max = array[0], min = array[0];
        for (int i : array) {
            if (i > max) {
                max = i;
            }
            if (i < min) {
                min = i;
            }
        }
        //count[]用于存储每个元素出现的次数
        int[] count = new int[max - min + 1];

        //统计出现的频次
        for (int i : array) {
            count[i - min] += 1;//数的位置 上+1
        }

        //创建最终返回的数组，和原始数组长度相等，但是排序完成的
        int[] result = new int[array.length];
        int index = 0;//记录最终数组的下标

        //先循环每一个元素  在计数排序器的下标中
        for (int i = 0; i < count.length; i++) {
            //遍历循环出现的次数
            for (int j = 0; j < count[i]; j++) {//count[i]:这个数出现的频率
                result[index++] = i + min;//以为原来减少了min现在加上min，值就变成了原来的值
            }
            System.out.println(Arrays.toString(result));
        }
    }
}