线性代数本质2：线性组合和线性相关和线性无关以及张成的空间

Posted 2021-10-14 快乐江湖

文章目录

• 一：基向量
• 二：线性组合
• 三：向量张成的空间
• 四：向量与点的关系
• 五：线性相关和线性无关

一：基向量

在$xy$直角坐标系中有一对非常特殊的向量

• $i$：指向$x$轴正方向的单位向量
• $j$：指向$y$轴正方向的单位向量

而$\left(\begin{array}{c}3\\ -2\end{array}\right)$这个向量的$x$和$y$坐标可以看作一个标量，它是单向向量$i$正向拉长为原来的3倍，把单位向量$j$反向拉长为原来的2倍

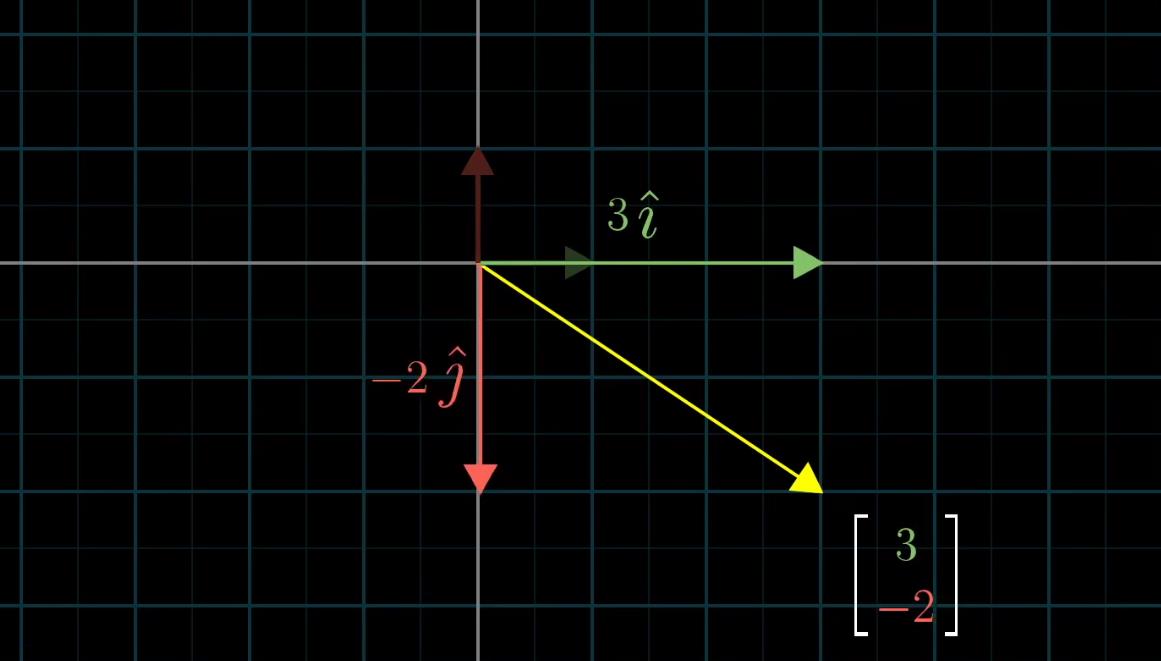
从这个角度上理解这个向量实际上是两个经过缩放的向量的和（注意这个概念非常重要）

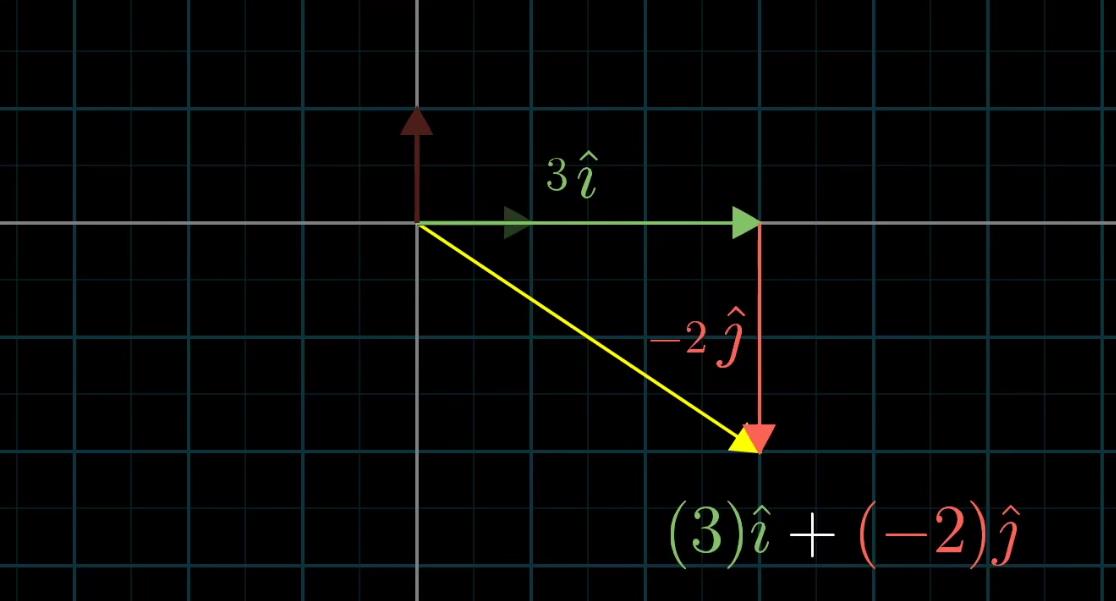
这里我们把$i$和$j$称为为$xy$坐标系的“基向量，合起来被称为坐标系的基”

这意味着当你把向量的分量看作标量时，那么基向量实际就是这些标量要缩放的对象

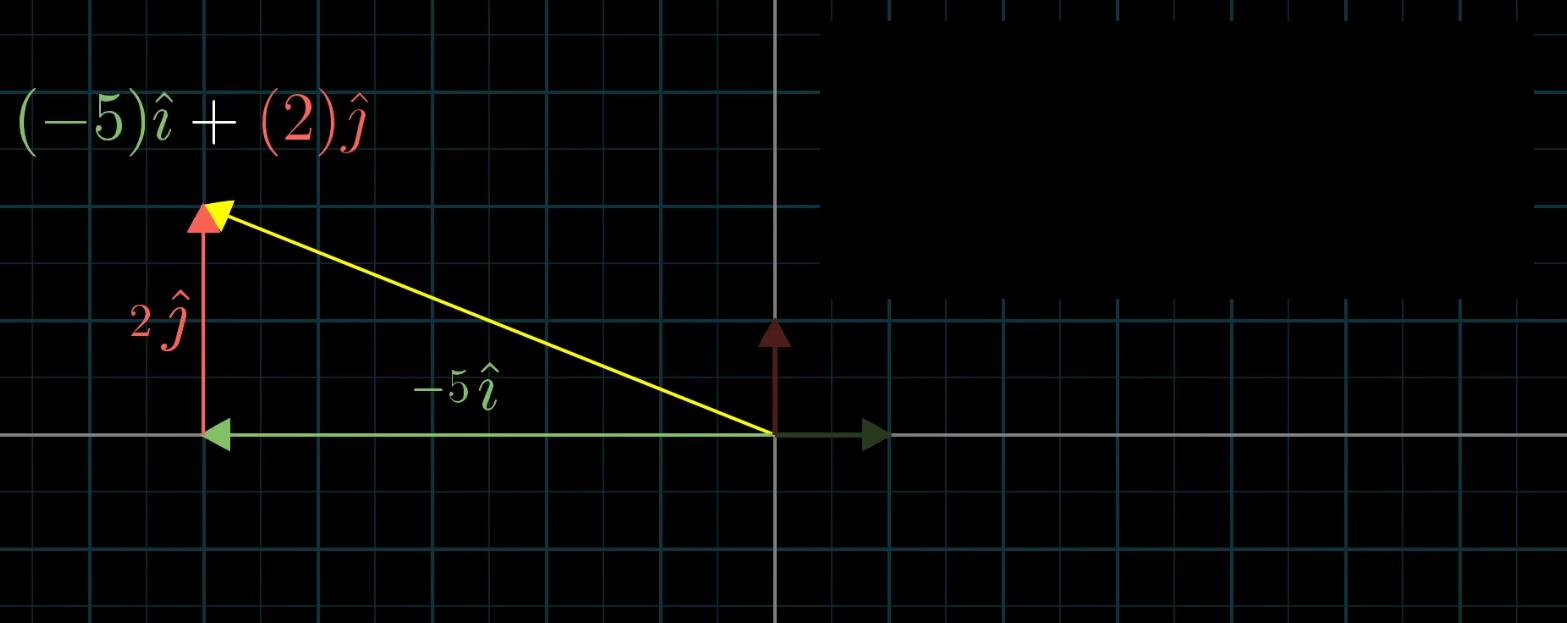
另外还需要注意的一点是：每当我们用数字描述向量时，它都依赖于我们正在使用的基。因为上面我们的举的例子是在一个非常特殊，非常普遍的情况，就是选择$xy$坐标系的$x$轴和$y$轴所在处作为基向量，那要是任选两个向量呢？当然也是可以的

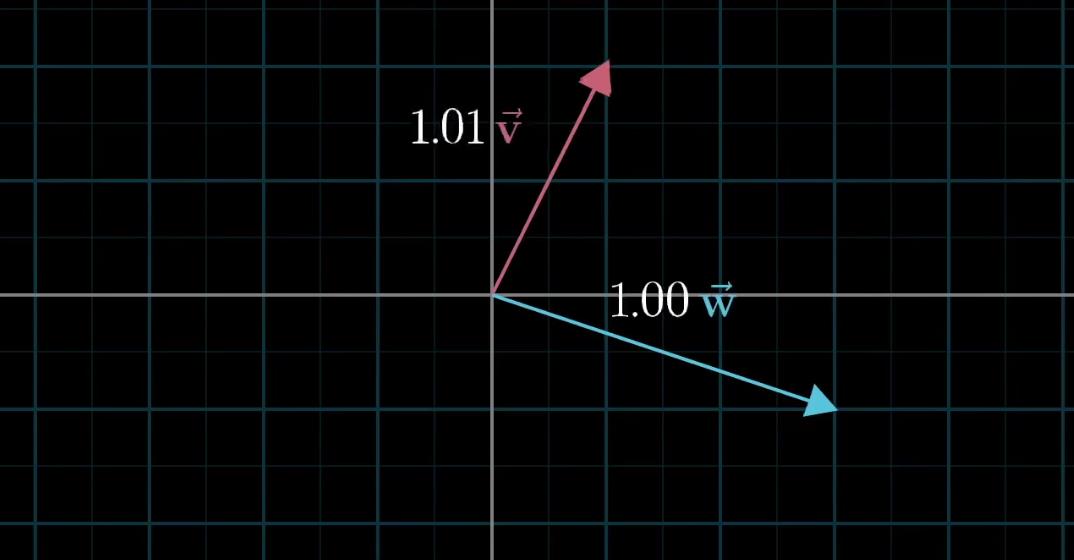
而且在这种情况下，通过标量缩放，这两个向量也可以表示二维平面内的任意向量

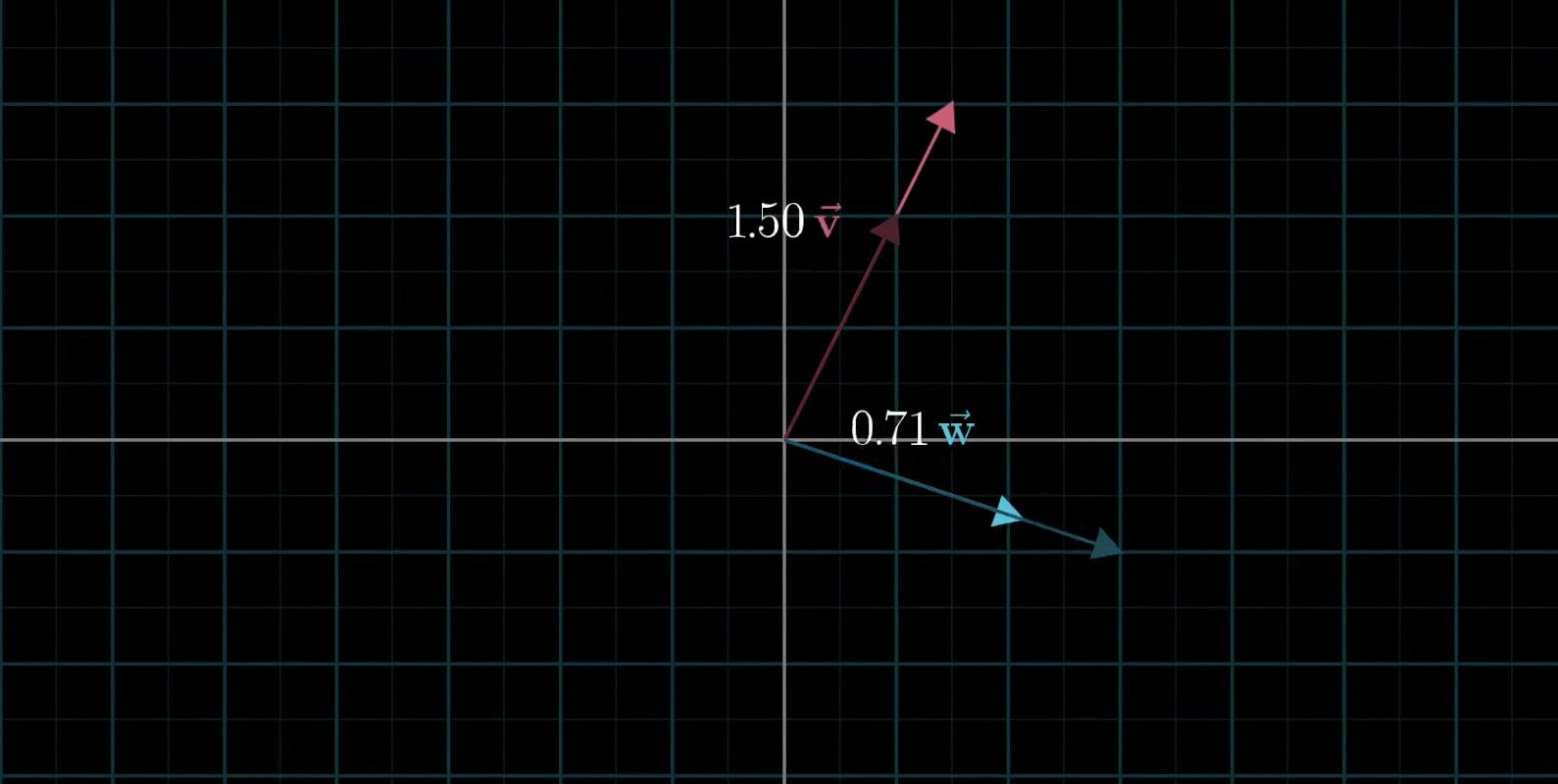
但是这种变换与之前我们描述的那个$i$和$j$的情况是完全不一样的，还是那句话：每当我们用数字描述向量时，它都依赖于我们正在使用的基

二：线性组合

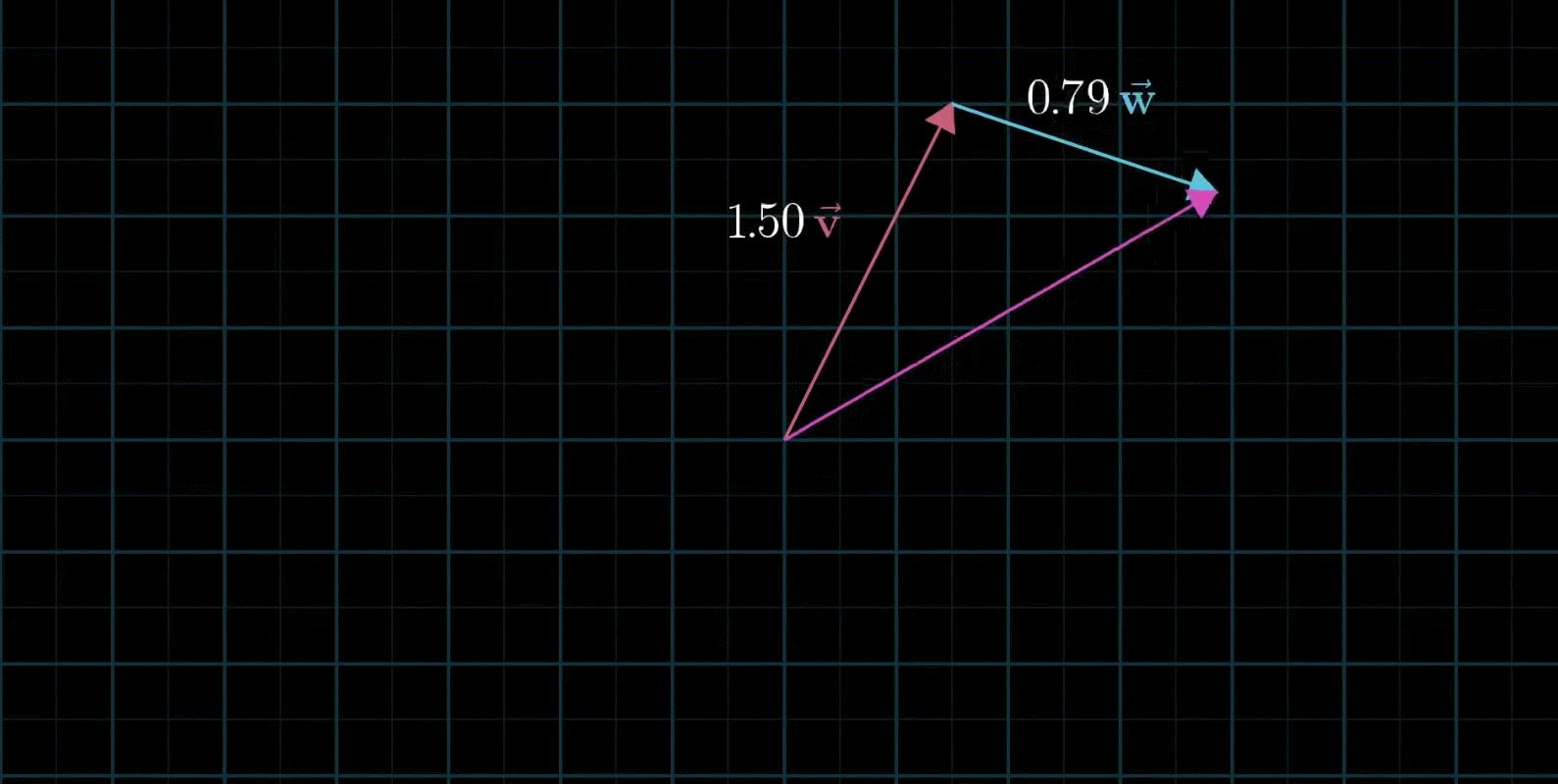
两个数乘向量的和称为这两个向量的线性组合

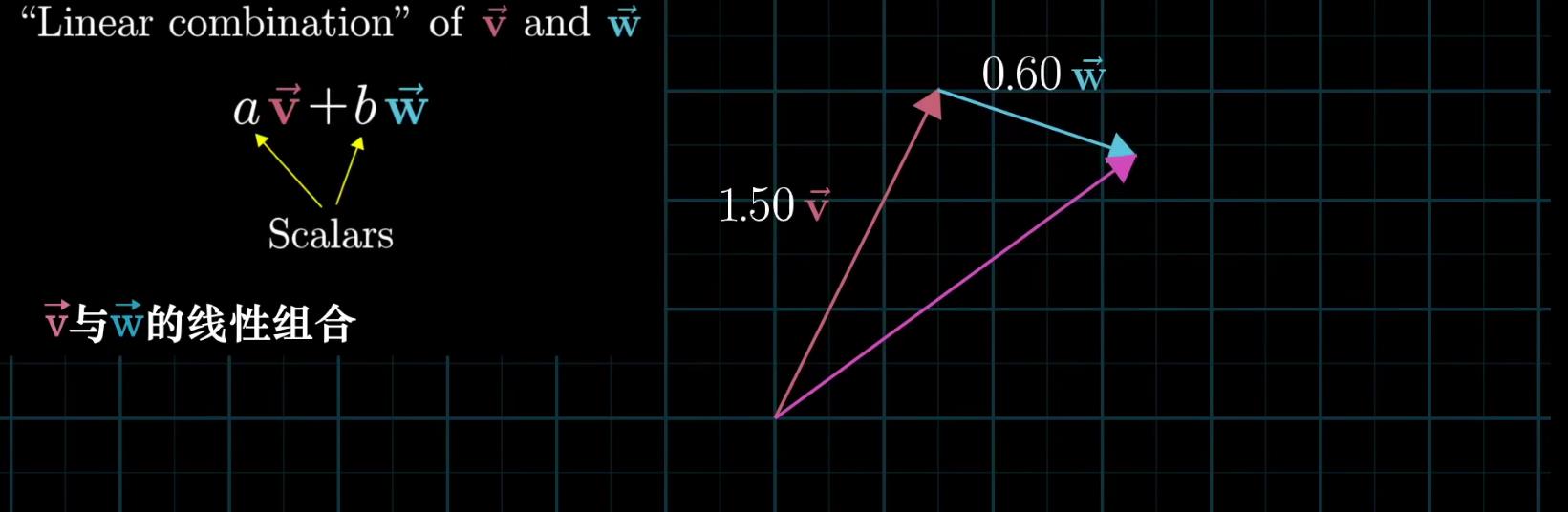
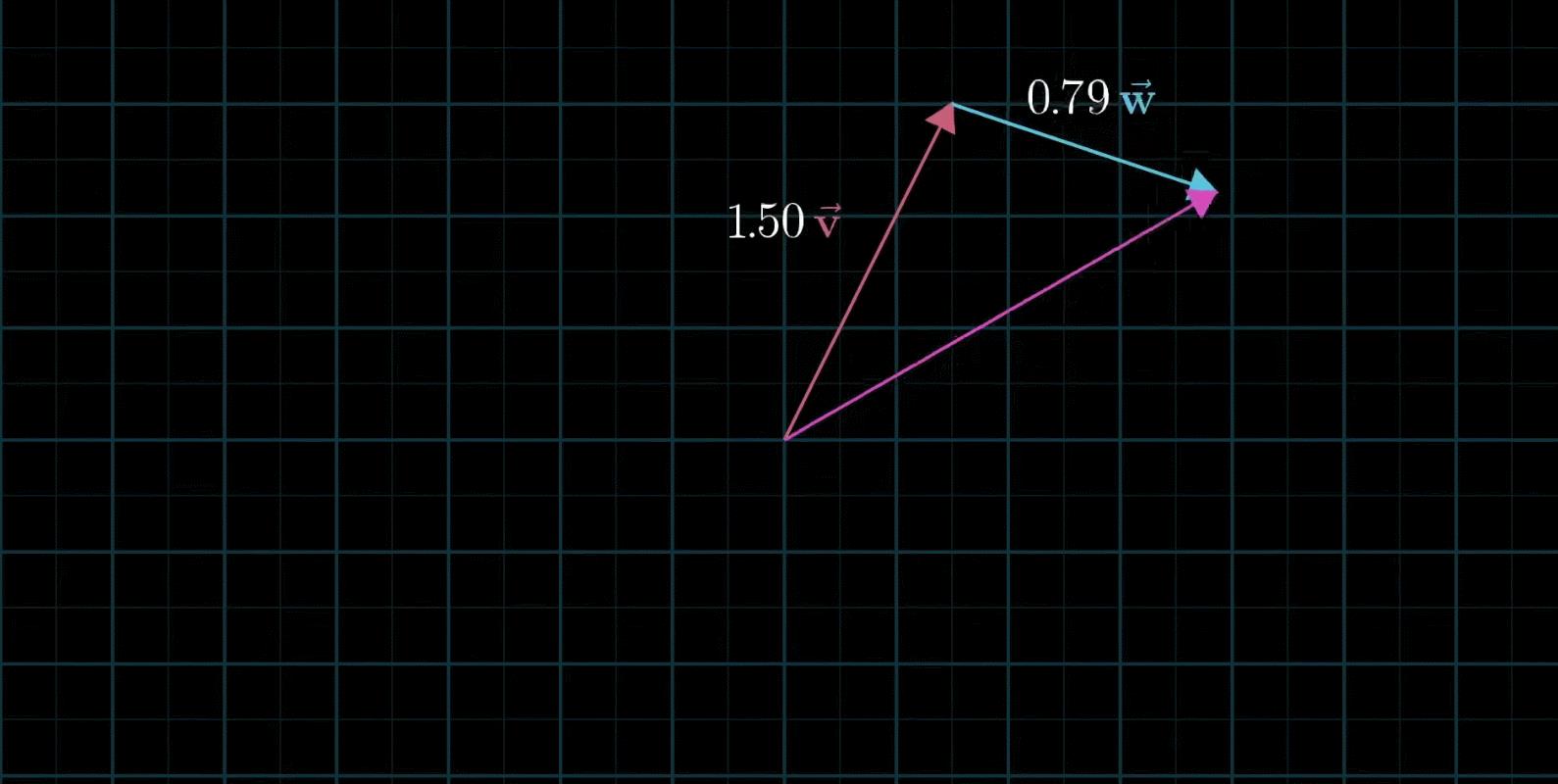
如果固定其中一个变量，让另外一个标量自由变换，那么所能表示的向量的终点会绘成一条直线

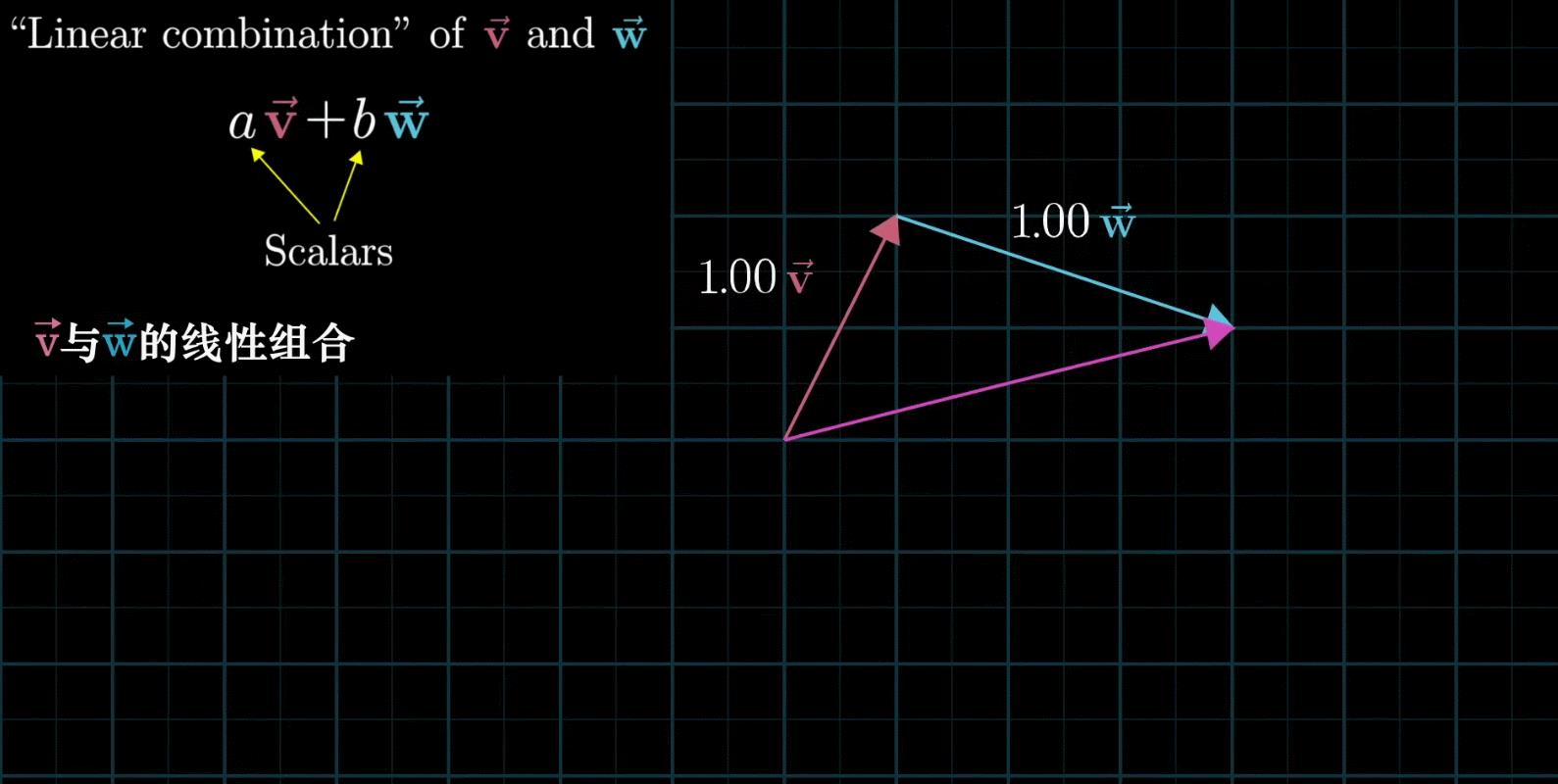
如果让两个标量都自由变换，那么会有以下几种情况：

• 在大多数情况下，对于一切初始向量，你能到达平面中任何一个点，所有二维向量尽在你的掌握之中
  

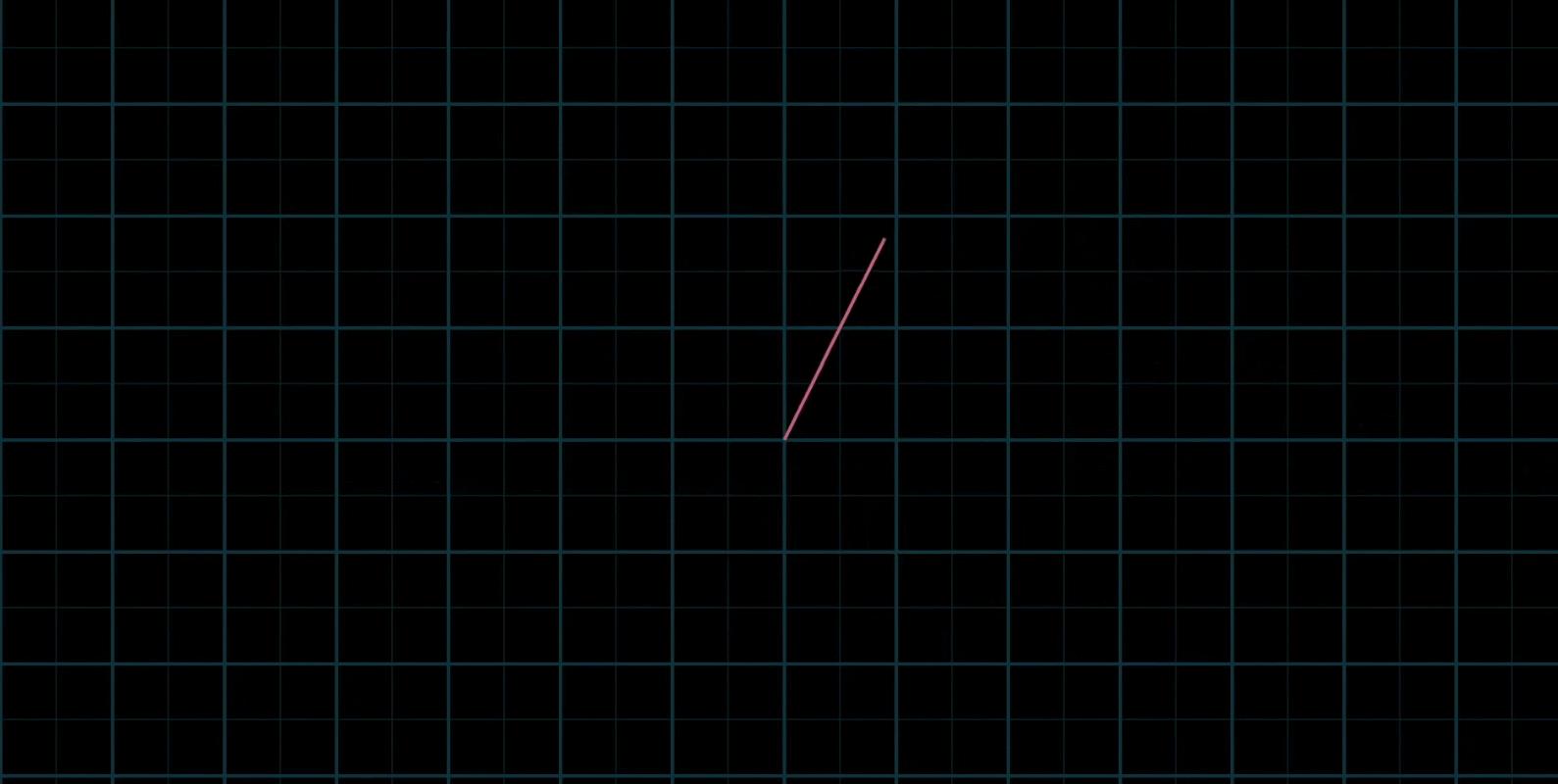
• 有时也会出现两个初始向量共线，那么所产生的新的向量的重点会被限制在一条过原点的直线上
  

• 还有，两个向量可能都是零向量，那么就只能呆在原地了
  

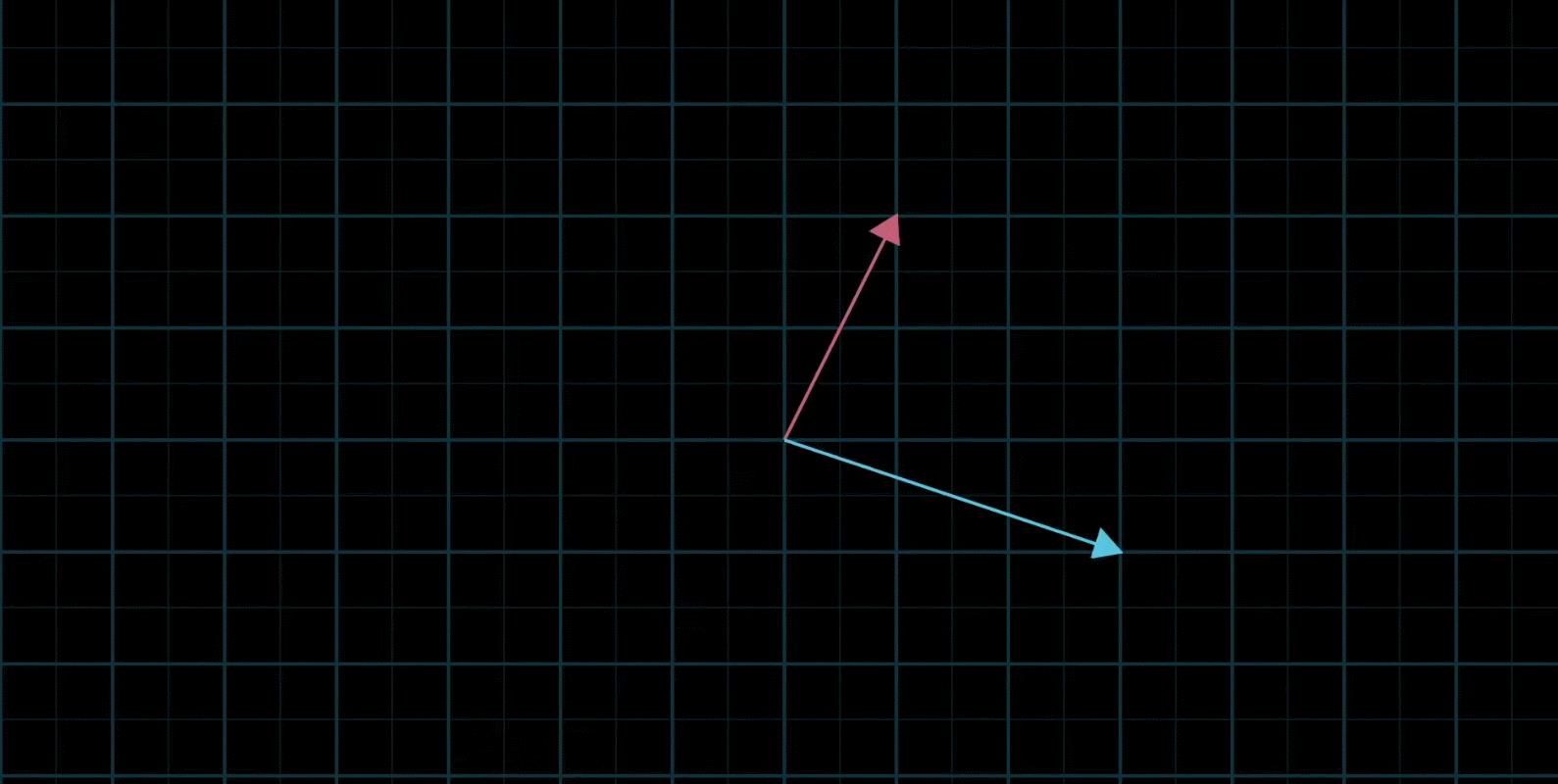
三：向量张成的空间

这里就可以引入一个概念——向量张成的空间：它是一个集合，这个集合表示了所有可以由给定向量通过线性组合表示的向量

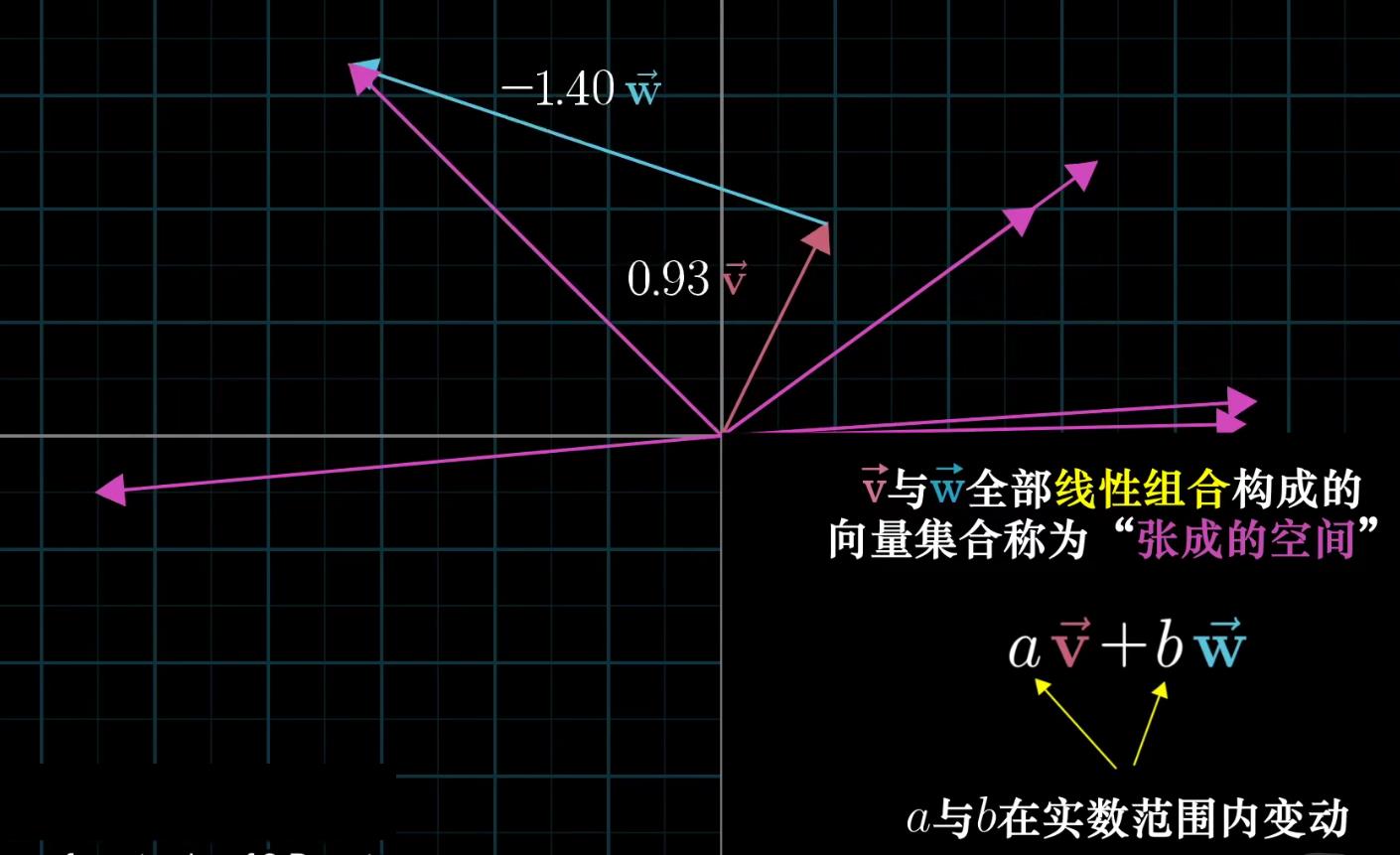
两个向量张成的空间实际上是提出了一个问题：仅通过向量加法和向量数乘这两种基础的运算，你能获得的所有向量的集合是什么？

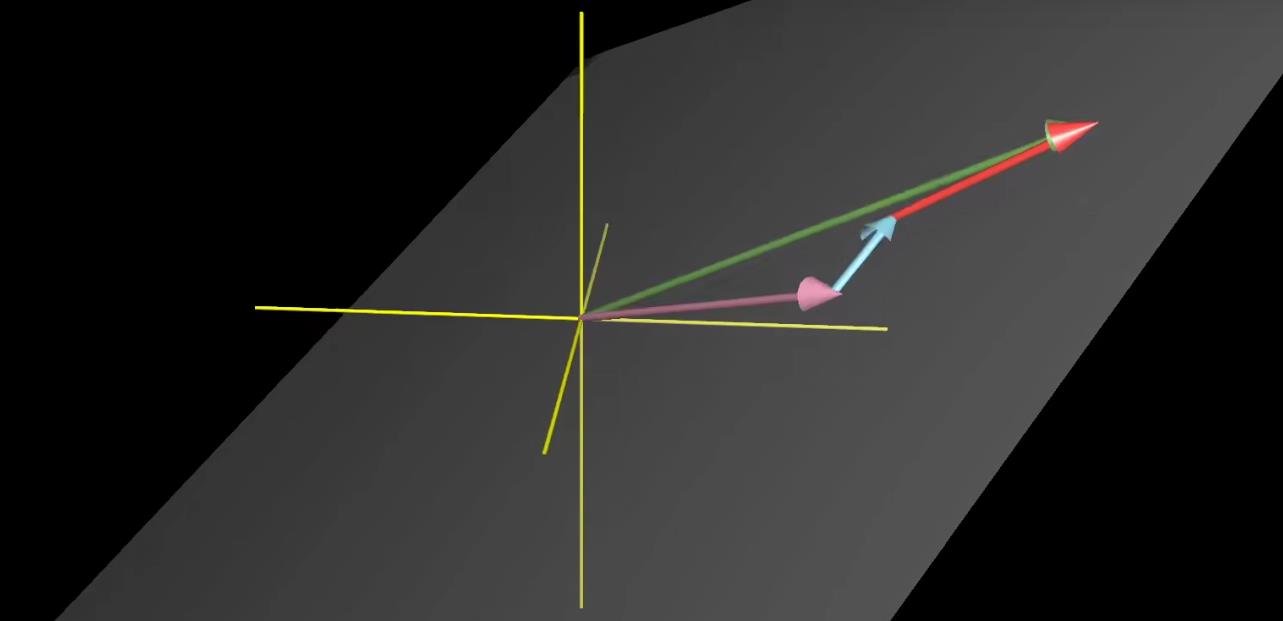
所以在三维空间中，取两个不同指向的向量，其张成的空间就是过某个原点的平面

如果将第三个向量让其落在前面两个向量张成的空间中，那么它们张成的空间将不会发生变化，或者通俗点说，这个向量就会被困在这个空间

四：向量与点的关系

一直到这里，我们对于向量的直观感受就是一个箭头，但其实点也是向量的一种表现形式

如果我们把所有二维向量铺满整个平面（用箭头），你会觉得异常拥挤

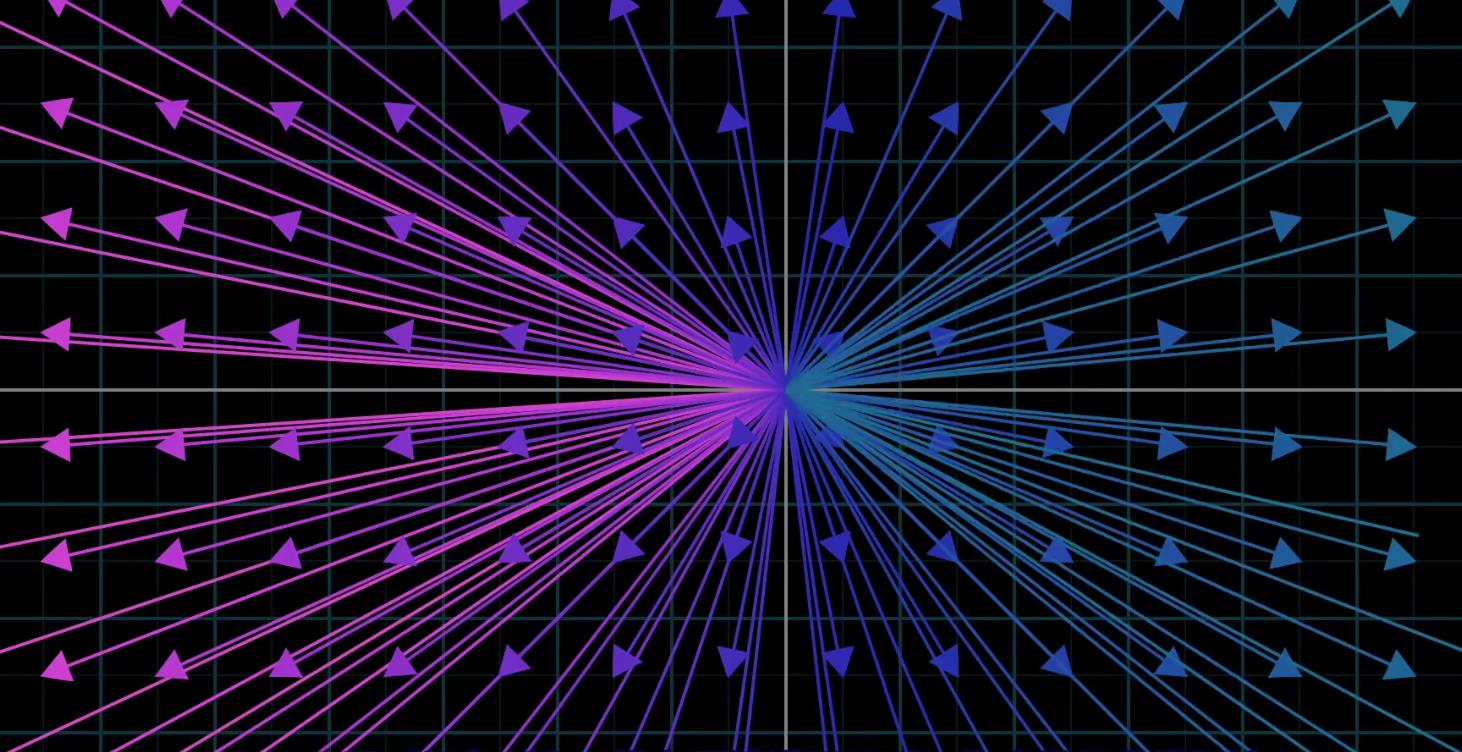
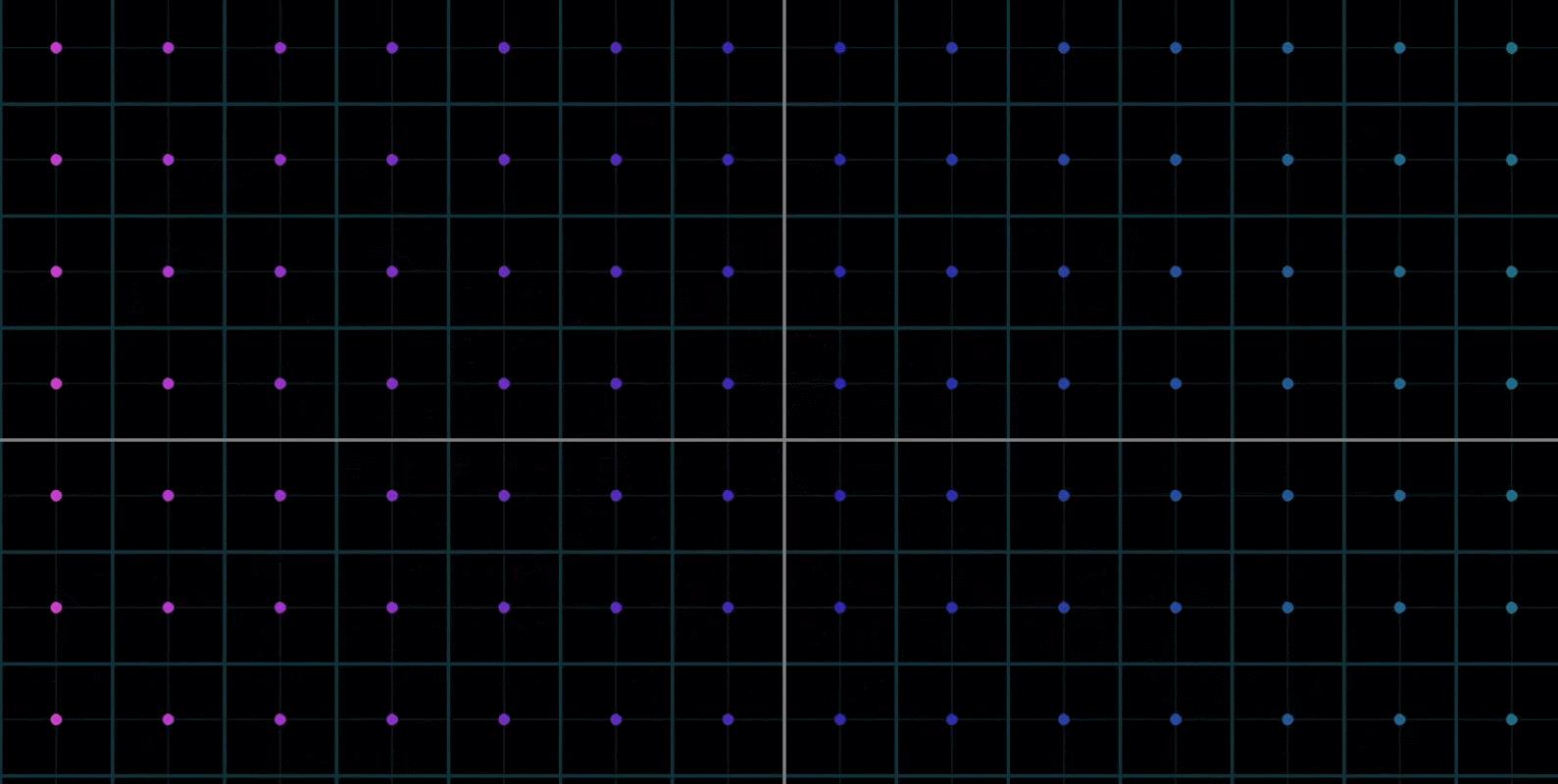
所以为了解决这个问题，让向量起点从原点开始，只保留每个向量的终点，这样的话箭头就退化成了点
这样的话当你在考虑落在一条直线上的所有向量时，只考虑直线本身即可

同样，你在考虑二维向量时，就不必关注箭头了，只需考虑点即可

注意我们在考虑单个向量时，最好还是用箭头

五：线性相关和线性无关

根据前面所述，在一组向量中，有个别向量是“多余的”，去掉它们，向量张成的空间不会减少，那么我们就称它们是线性相关的

反之，如果所有向量都给张成的空间增添了新的维度，那么我们就称它们是线性无关的

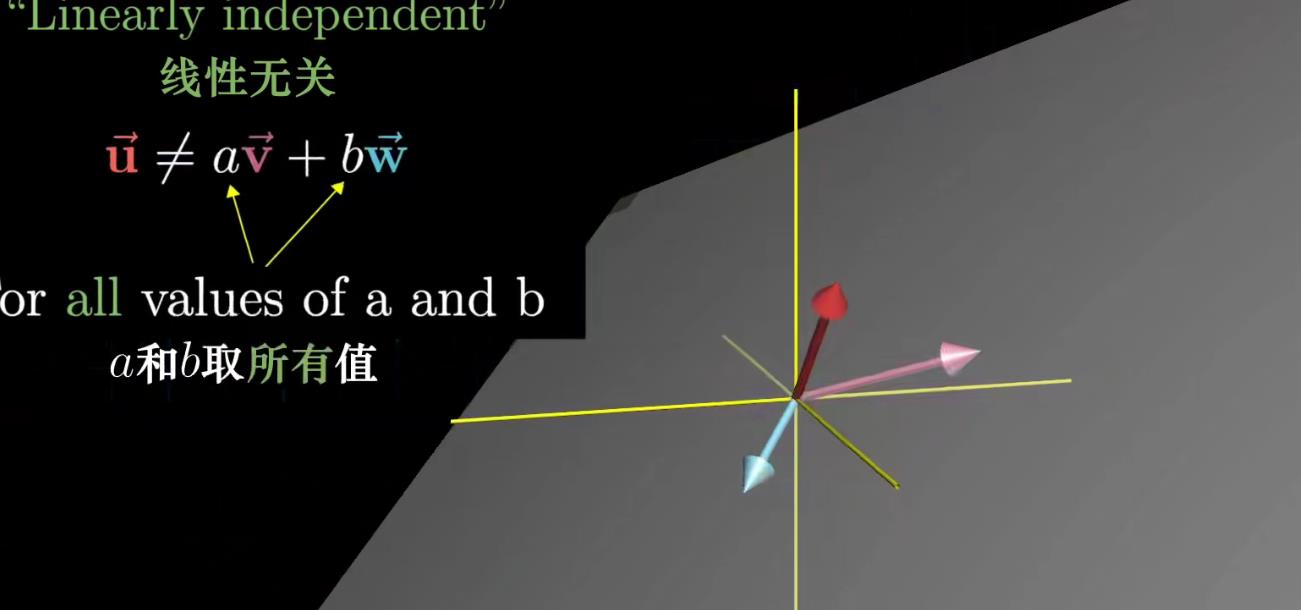
因此，向量空间的一组基是张成该空间的一个线性无关向量集合