线性代数本质3:矩阵和线性变换
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性代数本质3:矩阵和线性变换相关的知识,希望对你有一定的参考价值。
要说线性代数的精髓是什么?我认为就是本节的标题: 矩阵和线性变换的关系。
一:线性变换
“变换”其实是函数的一个别称,函数我们很熟悉,它会接受内容而输出结果

那么线性变换呢?所以我们考虑的是输入一个向量经过变换之后再输出对应的向量

那么既然变换就是函数,为什么不叫“线性函数”而叫线性变换呢?
其实,变换相对于函数来讲,它更具有一种运动的感觉,是在暗示你用运动的角度去思考向量的函数

- 输入向量移动到了输出向量的位置
第二个需要理解的就是线性二字,线性的对立面就是非线性,所以非线性变换的呈现在向量的感受就是下面这样
- 复平面
f
(
z
)
=
z
2
2
f(z)=\\frac{z^{2}}{2}
f(z)=2z2变换

- 复平面
f
(
z
)
=
e
z
f(z)=e^z
f(z)=ez变换

可以看出非线性变换是异常复杂的,但是幸运的是,这里讲的线性变换,将变换限制在了一种特定的类型上
如果一个变换具有以下两条性质,我们就称它是线性的
-
1:直线在变换后仍旧是直线,不能有所弯曲(下面动图是反例,直线被弯曲)

-
2:原点必须固定(下面是反例,直线虽然还是直线,但是原点移动了)
-
3:额外补充一点-对角线也不能弯曲(下面第一张图看起来好像是线性的,但是第二张图揭示了对角线弯曲了)

-

综上,线性变换必须是:保持网格平行且等距分布的变换
二:矩阵
可以发现,从图像上理解线性变换比较直观但是难以表达,既然线性代数的核心就是数字和空间的对应,那么我们如何使用数值去描述我们上面讲到的线性变换呢?
- 其实线性代数的一个经典例子就是游戏和动画——你想要让一个角色移动到某个位置后或者其自身发出怎样的动作,你能给出什么样的计算公式,依次得到变换后的坐标呢?

比如现在有一个向量
(
−
1
2
)
\\begin{pmatrix} -1\\\\ 2\\end{pmatrix}
(−12),根据上一篇文章所提到的,它就是就是基向量
i
j
ij
ij的线性组合

假如现在我们施加一个线性变换如下

大家可以看到这里变换之后,
v
‾
\\overline v
v和
i
j
ij
ij都发生了变换,都不是以前的
v
v
v和
i
j
ij
ij,那么由于线性变换会保证网格线平行且等距分布,所以变换后的
v
v
v的位置是-1与变换后
i
i
i之积+2与变换后
j
j
j之积
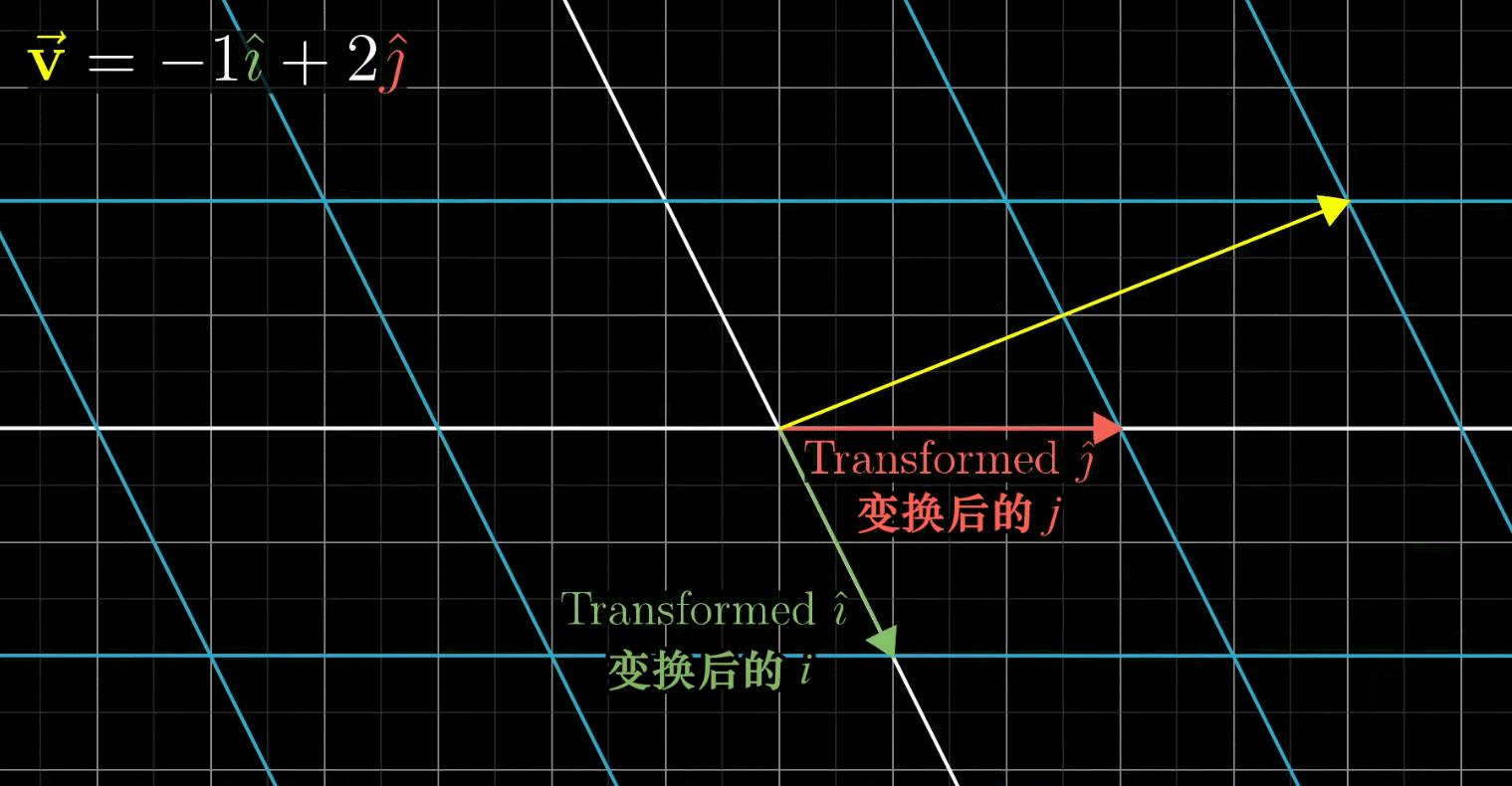
或者换句话说:既然
v
‾
\\overline v
v是
i
j
ij
ij的特定的线性组合,那么变换后的
v
‾
\\overline v
v也是变换后的
i
j
ij
ij的特定的线性组合
这一点非常重要:你可以只根据变换后的 i j ij ij推断出变换后的 v ‾ \\overline v v
在上图所示的情形中变换后的向量 i j ij ij分别为 ( 1 − 2 ) \\begin{pmatrix} 1\\\\ -2\\end{pmatrix} (1−2)和 ( 3 0 ) \\begin{pmatrix} 3\\\\ 0\\end{pmatrix} (30),于是,变换后的 v ‾ \\overline v v=-1 ( 1 − 2 ) \\begin{pmatrix} 1\\\\ -2\\end{pmatrix} (1−2)+2 ( 3 0 ) \\begin{pmatrix} 3\\\\ 0\\end{pmatrix} (30)= ( − 1 ( 1 ) + 2 ( 3 ) − 1 ( − 2 ) + 2 ( 0 ) ) \\begin{pmatrix} -1(1)+2(3)\\\\ -1(-2)+2(0)\\end{pmatrix} (−1(1)+2(3)−1(−2)+2(0))= ( 5 2 ) \\begin{pmatrix} 5\\\\ 2\\end{pmatrix} (52),于是变换后的 v ‾ \\overline v v一定落在 ( 5 2 ) \\begin{pmatrix} 5\\\\ 2\\end{pmatrix} (52)处

以上是关于线性代数本质3:矩阵和线性变换的主要内容,如果未能解决你的问题,请参考以下文章