CS224W摘要08.Applications of Graph Neural Networks

Posted 2021-10-14 oldmao_2000

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了CS224W摘要08.Applications of Graph Neural Networks相关的知识，希望对你有一定的参考价值。

CS224W: Machine Learning with Graphs
公式输入请参考：在线Latex公式
这节课要讲如何对图做augmentation
之前的讨论都是根据原始的图数据进行计算的，也就是说之前都是根据以下假设进行的：
Raw input graph = computational graph
但是实际上这个假设有很多问题：

Features:
§ The input graph lacks features
Graph structure:
§ The graph is too sparse →inefficient message passing
§ The graph is too dense →message passing is too costly（某些微博节点关注量上百万，做aggregation计算量太大）
§ The graph is too large →cannot fit the computational graph into a GPU

因此原始数据不一定适用直接进行计算，要对原始的图数据进行增强（处理）。
针对上面的两个方面问题，这节课也从两个方面进行讲解如何做增强。
Graph Feature augmentation
Graph Structure augmentation
§ The graph is too sparse →Add virtual nodes / edges
§ The graph is too dense →Sample neighbors when doing message passing
§ The graph is too large →Sample subgraphs to compute embeddings

Graph Feature augmentation

原因：
1.节点没有feature，只有结构信息（邻接矩阵）
解决方案：
a）Assign constant values to nodes

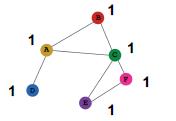
b）Assign unique IDs to nodes，一般使用独热编码

两个方案的对比如下表：

	方案a	方案b
Expressive power	Medium. All the nodes are identical, but GNN can still learn from the graph structure	High. Each node has a unique ID, so node-specific information can be stored
Inductive learning (Generalize to unseen nodes)	High. Simple to generalize to new nodes: we assign constant feature to them, then apply our GNN	Low. Cannot generalize to new nodes: new nodes introduce new IDs, GNN doesn’t know how to embed unseen IDs
Computational cost	Low. Only 1 dimensional feature	High. O（V） dimensional feature, cannot apply to large graphs
Use cases	Any graph, inductive settings (generalize to new nodes)	Small graph, transductive settings (no new nodes)

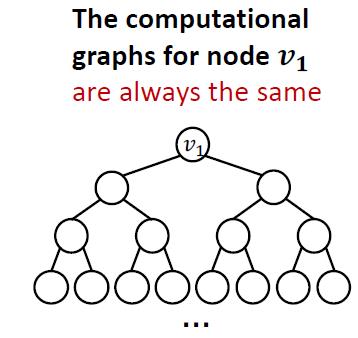
2.有些图结构GNN很难学习到，例如：Cycle count feature

两个图中的 $v_1$ 节点度都为2，以 $v_1$ 节点做出来的计算图都是一样的二叉树

解决方案是把cycle count直接作为特征加到节点信息里面

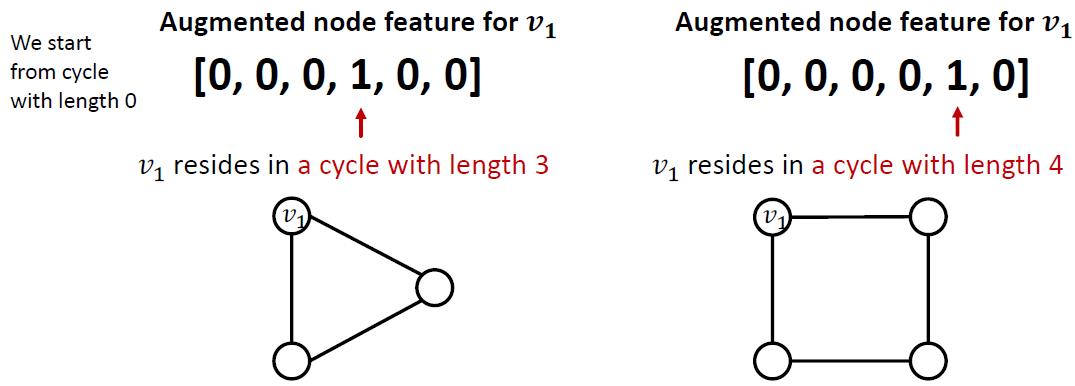
当然还可以有别的特征可以加进来，例如：
§ Node degree
§ Clustering coefficient
§ PageRank
§ Centrality

Graph Structure augmentation

Augment sparse graphs

Add virtual edges

Connect 2-hop neighbors via virtual edges
该法与计算图的邻接矩阵： $A+A^2$ 效果一样
例如：Author-to-papers的Bipartite graph中

2-hop virtual edges make an author-author collaboration graph.

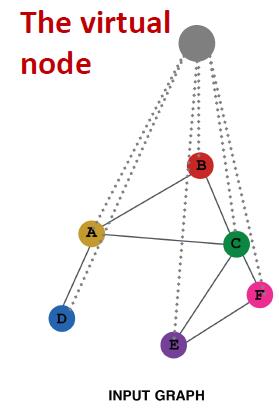
Add virtual nodes

The virtual node will connect to all the nodes in the graph.
§ Suppose in a sparse graph, two nodes have shortest path distance of 10.
§ After adding the virtual node, all the nodes will have a distance of two.
好处：
Greatly improves message passing in sparse graphs.

Augment dense graphs

方法就是对邻居节点进行采样操作。
例如，设置采样窗口大小为2，那么

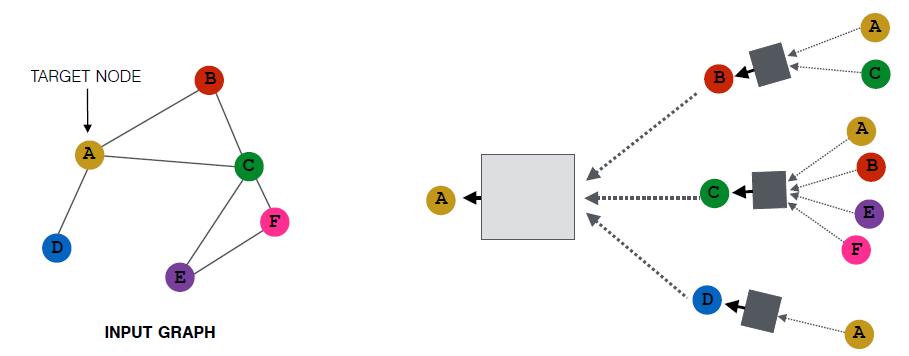
可能变成：

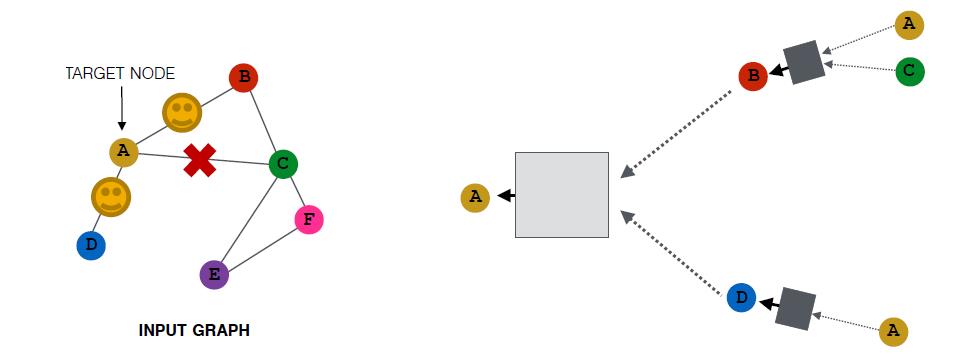
当然，采样是随机的，所有还有可能是：

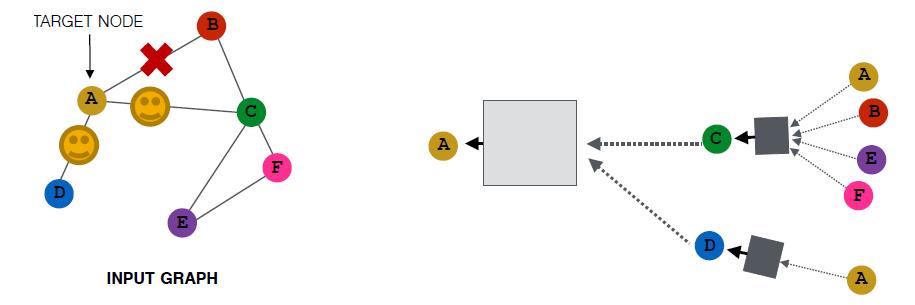
当然，如果邻居节点个数小于采样窗口大小，汇聚后的embedding会比较相似。
这个做法的好处是大大减少计算量。

Prediction with GNNs

这个小节讲解GNN框架的预测部分：

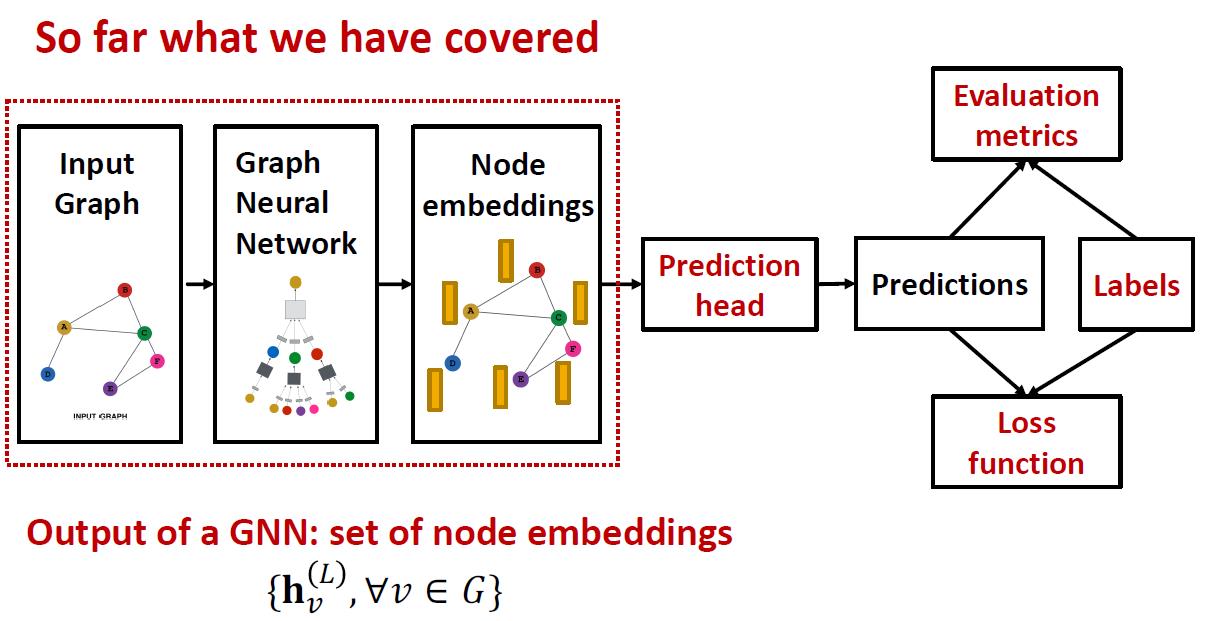
GNN Prediction Heads

Idea: Different task levels require different prediction heads
这里第一次看到用Head来代表函数

Node-level prediction

直接用节点表征进行预测
Suppose we want to make 𝑘-way prediction
§ Classification: classify among 𝑘 categories
§ Regression: regress on 𝑘 targets

$\\hat y_v=Head_{node}h_v^{(L)}=W^{(H)}h_v^{(L)}$

Edge-level prediction

用一对节点的表征对边进行预测：
$\\hat y_{uv}=Head_{edge}(h_u^{(L)},h_v^{(L)})$
这里的Head有两种做法：
1.Concatenation + Linear

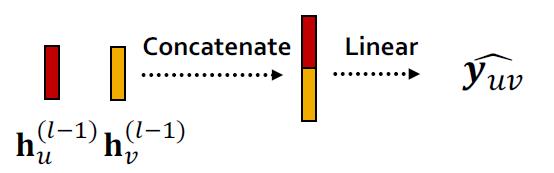
$\\hat y_{uv}=Linear(Concat(h_u^{(L)},h_v^{(L)}))$
这里的Linear操作会将2×d维的concat结果映射为 k-dim embeddings（相当于𝑘-way prediction）
2.Dot product
$\\hat y_{uv}=(h_u^{(L)})^Th_v^{(L)}$
由于点积后得到的是常量，因此该方法用于𝟏-way prediction，通常是指边是否存在。
如果要把这个方法用在𝒌-way prediction，则可以参考多头注意力机制设置k个可训练的参数： $W^{(1)},W^{(2)},\\cdots,W^{(k)}$
$\\hat y_{uv}^{(1)}=(h_u^{(L)})^TW^{(1)}h_v^{(L)}\\\\ \\cdots\\\\ \\hat y_{uv}^{(k)}=(h_u^{(L)})^TW^{(k)}h_v^{(L)}$
$\\hat y_{uv}=Concat(y_{uv}^{(1)},\\cdots,y_{uv}^{(k)})$

Graph-level prediction

使用图中所有节点的特征做预测。
$\\hat y_G=Head_{graph}(\\{h_v^{(L)}\\in \\R^d,\\forall v\\in G\\})$
这里的head函数和aggregation操作很像，也是有mean、max、sum操作。
这些常规操作对于小图效果不错，对于大图效果不好，会掉信息。
例子：
we use 1-dim node embeddings
§ Node embeddings for $𝐺_1: \\{−1,−2, 0, 1, 2\\}$