Openjudge 7215 简单的整数划分问题

Posted 2021-10-14 超霸霸

Openjudge 7215 简单的整数划分问题

• 题目要求：
  

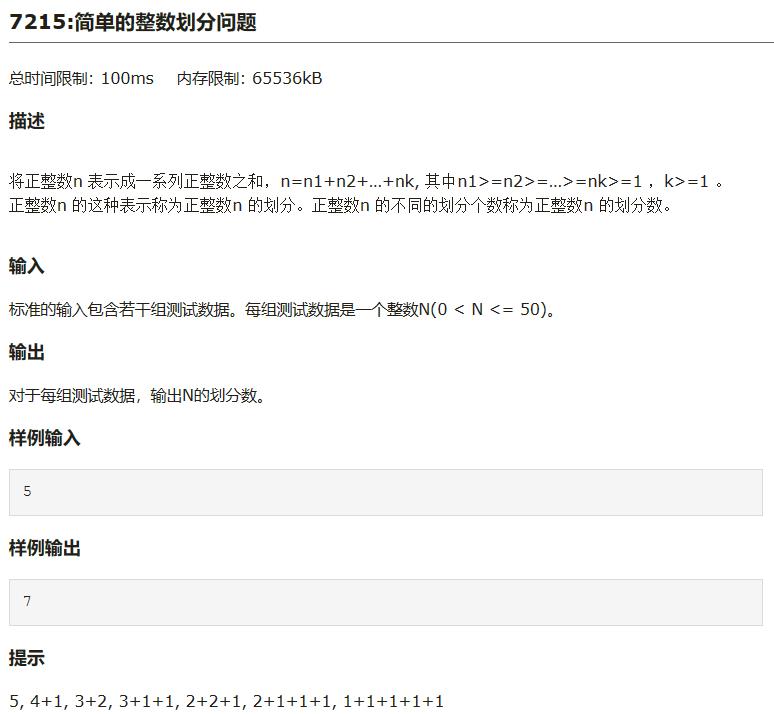
• 递归方法求解：

#include<iostream>
using namespace std;

int fun(int n, int m)
{
	if (n == 1 || m == 1)
	{
		return 1;
	}
	else if (n < m)
	{
		return fun(n, n);
	}
	else if (n == m)
	{
		return 1 + fun(n, m - 1);
	}
	else if (n > m)
	{
		return fun(n - m, m) + fun(n, m - 1);
	}
}

int main()
{
	int n;
	while (cin >> n)
	{
		cout << fun(n, n) << endl;
	}
	return 0;
}

• 思路解析：

//1.变量含义
代码中n代表输入的数，在函数fun中代表该情况下的总和sum，而m代表组成sum的数组中的最大值max
例如：当n=6，m=4时，既sum=6,max=4，组成6的数组如：[4,1,1]、[4,2]中的最大值为4，该情况的解为2

//2.各种情况下的求解
* 当n=1时，组成n的数组只有[1]，所以n=1时，f(n,x)=1 （x为任意值）
* 当m=1时，无论n为何值，组成n的数组只有[1,1,.....]（n个1），所以m=1时，f(n,1)=1 （n为任意值）
* 当n=m时，既第一次调用函数时，可以分为两种情况：
	* max=m：只有一种情况，既[n]，所以该值为1
	* max<m：即为f(n,m-1)的值
	所以当n=m时，f(n,m)=1+f(n,m-1)
* 当n>m时，可以分为两种情况：
	* max=m：此时组成n的数组的格式为[m,(x1,x2....)]（m为最大值，m后面的参数个数不确定，但它们的和为n-m，(x1+x2+....)=n-		m，且(x1,x2....)中的最大值max一定小于等于m）所以求该情况下的f(n,m)的值就转化成了求数组[x1,x2....]（sum=n-m,max<=m）的	  解的个数，即求f(n-m,m)的值
	举个例子：假设n=6,m=4，即求解[4,(x1,x2....)]有多少种情况，即求解[x1,x2....](sum=2,max<=4)有多少种情况，即求解f(2,4)的	 值
	* max<m：即为f(n,m-1)的值
	所以当n<m时，f(n,m)=f(n-m,m)+f(n,m-1)
* 当n<m时，组成n的数组中最大值max在任何情况下一定小于等于n，所以max>n的情况的解不存在，即f(n,m)=f(n,n)

综上：
          1		                     (n=1 || m=1)
f(n,m)=   fun(n, n)		             (n < m)
		  1 + f(n, m - 1)		     (n==m)
		  f(n - m, m) + f(n, m - 1)	 (n>m)