解题报告 合并果子

Posted 2021-10-14 没头发的米糊

题目来源

洛谷P1090　 [NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G - 洛谷

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

输入输出格式

输入格式：

输入文件fruit.in包括两行，第一行是一个整数n(1<＝n<=10000)，表示果子的种类数。第二行包含n个整数，用空格分隔，第i个整数ai(1<＝ai<=20000)是第i种果子的数目。

输出格式：

输出文件fruit.out包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于2^31。

输入输出样例

输入样例#1：

3

1 2 9

输出样例#1：

15

说明

对于30％的数据，保证有n<=1000：

对于50％的数据，保证有n<=5000；

对于全部的数据，保证有n<=10000。

解题思路

         这道题比较典型的解法是使用贪心+二叉堆来解决，每次找两个最小的堆进行合并，重复n-1次，那么这样消耗的体力一定是最少的。如何找到两个最小的堆呢？一种思路是每次都打擂台，找出最小的两个堆，但这样显然慢，时间复杂度达到。因此需要考虑更好的算法，由于这是一道处理动态变化数据大小关系的题目，很容易想到二叉堆。于是问题得解。

具体解法

      首先从题目条件入手，需要一个小顶堆作为数据结构。怎么整？是现场写吗？可以，但不够快。二叉堆实际可以用来实现优先队列，因此就可以直接使用C++STL中的优先队列来完成这个任务，省去写二叉堆的痛苦。

附：STL中的优先队列 定义：priority_queue <Type, Container, Functional> Type  数据类型 Container  容器类型 Functional  比较方式 当需要用自定义的数据类型时才需要传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大顶堆。

         在创建完小顶堆以后，读入数据，将所有元素丢进小顶堆中，然后开始循环合并果子。

         每次循环时寻找最小的两堆果子，即直接出队两次，然后入队两次元素的和，如此往复，直至只剩一堆果子为止。于是此题得解。

         本题采用二叉堆是一种理想的思路，但面对刁钻的数据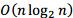，可能仍然不够快。洛谷上还有的解法，但本题解强调的是堆的使用，因此不再赘述。

代码实现

1.	#include <iostream>
2.	#include <queue>
3.	#include <algorithm>
4.	using namespace std;
5.	priority_queue< int, vector<int>, greater<int> > q;
6.	int main()
7.	{
8.	 int n,i,x,t,ans=0;
9.	 cin >> n;
10.	 for(i=1;i<=n;i++)
11.	 {
12.	  cin >> x;
13.	  q.push(x);
14.	 }
15.	 while(--n)
16.	 {
17.	  t = 0;
18.	  t += q.top(); q.pop();
19.	  t += q.top(); q.pop();
20.	  ans += t;
21.	  q.push(t);
22.	 }
23.	 cout << ans << endl;
24.	 return 0;
25.	}