☀️~算法系列之爆肝万字总结七种查找算法，持续补充更新中，建议收藏~☀️

Posted 2021-10-14 Roninaxious

🍅 作者主页：Roninaxious
🍅 欢迎点赞 👍 收藏 ⭐留言 📝
🍅 话不多说 🍁开卷！

• 🚢 顺序查找算法
• 🚢 二分查找算法
• • 💥优化二分查找算法
• 🚢 插值查找算法
• 🚢 斐波那契查找算法

---

🚢 顺序查找算法

🙄对于顺序查找算法比较容易理解，遍历一个数组即可，如果找到该值返回对应的下标即可.🙄

🧧源代码🧧

    /**
     * 如果返回的是-1，则数组中无相关值
     * @param arr 待搜索数组
     * @param value 待搜索值
     * @return -1或者 索引值
     */
    private static int seqSearch(int[] arr, int value) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == value) {	//如果找到对应的值
                return i;			//返回对应的索引
            }
        }
        return -1;				//没有找到返回-1
    }

🎐测试代码🎐

    public static void main(String[] args) {
        int[] arr = {1, 34, -1, 5, 8, 2, 99};
        int index = seqSearch(arr, 8);
        if (index == -1) {
            System.out.println("无相关值!");
        } else {
            System.out.println("改值对应的索引下标为:"+index);
        }
    }

---

🚢 二分查找算法

🙄对于某一个数组arr(这个数组是有序的,假设是升序)，我们想要从数组中找到值value，返回它对应得索引
begin = 0;
end = arr.length
mid = (begin+end)/2
这三个变量begin、mid、end对应这数组的下表
1.我们将value与arr[mid]进行比较
2.如果value > arr[mid]，那么我们只需要在mid的右边进行搜索即可；如果value < arr[mid]，我们只需要在mid的左边进行搜索即可.
🙄
🎐注意点🎐
Ⅰ.如果数组不是有序的，则需要将其进行排序后再操作
Ⅱ.使用递归能够很好实现

二分查找需要一定的递归知识

【☀️_{爆肝万字总结递归}❤️玩转算法系列之我如何才能掌握递归解题的能力❤️_{十大经典问题助你突破极限}☀️】:https://blog.csdn.net/Kevinnsm/article/details/120445071?spm=1001.2014.3001.5501

🧧源代码🧧

    /**
     *二分查找算法
     * @param arr 待搜索的数组
     * @param value 待查找的值
     * @param begin 左边的索引
     * @param end   右边的索引
     * @return 如果找到该值，就返回其对应的下标，否者返回其-1
     */
    private static int binarySearch(int[] arr, int value, int begin, int end) {
        if (begin > end) {
            return -1;
        }
        int mid = (begin + end) / 2;            //取中间值
        if (value > arr[mid]) {
            return binarySearch(arr, value, mid + 1, end);
        } else if (value < arr[mid]) {
            return binarySearch(arr, value, begin, mid - 1);
        } else {
            return mid;
        }
    }

🎐测试代码🎐

    public static void main(String[] args) {
        int[] arr = {1,3, 4, 5, 8, 11, 23, 77};
        int index = binarySearch(arr, 8, 0, arr.length - 1);
        if (index == -1) {
            System.out.println("未找到该值!");
        } else {
            System.out.println(index);
        }
    }

💥优化二分查找算法

❤️如果一个数组是[1,2,4,5,6,8,8,8,8,11,23]，一旦查找其他的8，那么如果使用上面的查找算法，就只能返回一个索引值；因此，对该查找算法进行优化，让其能够返回所有的索引值❤️

     /**
     * 默认是升序数组
     * 对上部分进行优化，能够查出重复数据的所有下表
     * @param arr 待搜索数组
     * @param value 待查询的值
     * @param begin 左索引
     * @param end   右索引
     * @param list  存储搜索值下表的集合
     */
    private static void binarySearch2(int[] arr, int value, int begin, int end, List<Integer> list) {
        if (begin > end) {                  //递归结束条件
            return;
        }
        int mid = (begin + end) / 2;         //取中值
        if (value > arr[mid]) {         //说明需要去mid右边查找
            binarySearch2(arr, value, mid + 1, end, list);  //递归进入 mid+1 至 end这一段数据
        } else if (value < arr[mid]) {   //说明需要去mid左边查找
            binarySearch2(arr, value, begin, mid - 1, list); //递归进入 begin 至 mid-1这一段数据
        } else if (value == arr[mid]) {     //说明找到了待查找的值；此时需要考虑的是在这个值的左边和右边可能有相同的数据
            int tempFront = mid - 1;        //例如arr [1,8,8,8,9],找到arr[2],它的前后都有8，所以需要进行判断
            while (true) {          //这个while循环是对arr[2]左边进行判断是否有8
                if (tempFront < 0 || value != arr[tempFront]) { //这当上面的mid为0时，这个tempFront为-1，所以需要进行判断
                    break;                                      //又或者左边第一个就不等于value，那么直接break即可
                }
                list.add(tempFront);        //将符合value=8的索引值加入到list集合中
                tempFront--;
            }
            list.add(mid);              //将arr[2]加入到集合中，至于为什么现在加入是因为按照从大到小 list[2,3,4]
            int tempAfter = mid + 1;
            while (true) {          //右边类似于左边
                if (tempAfter > end || value != arr[tempAfter]) {
                    break;
                }
                list.add(tempAfter);
                tempAfter++;
            }
        }
    }

🎐测试代码🎐

    public static void main(String[] args) {
        int[] arr = {1,3, 4, 5, 5, 5, 5, 11, 23, 77};
        List<Integer> list = new ArrayList<>();
        binarySearch2(arr, 5, 0, arr.length - 1, list);
        if (list.isEmpty()) {
            System.out.println("未找到该值!");
        } else {
            System.out.println(list.toString());
        }

    }

🥫分析以上的二分查找算法

根据它的 int mid = (begin+end)/2 ，我们可以推算二分算法适用于什么场景；
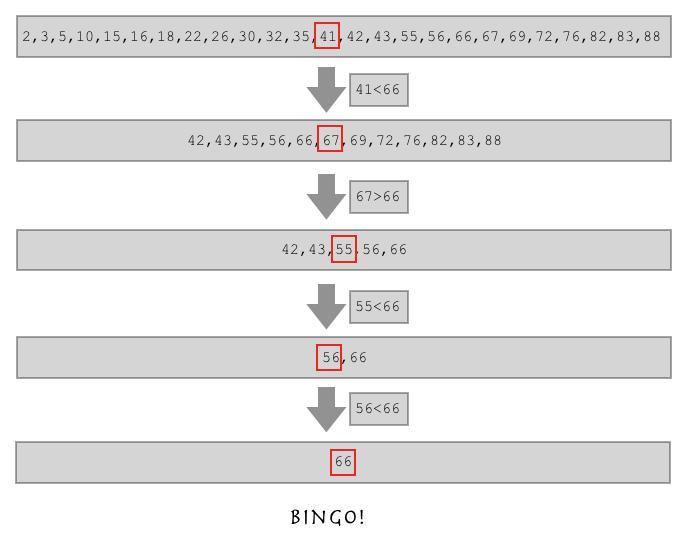
假设一个数组为arr[1,2,3,4,5…,98,99,100] ，我们要找寻1这个值，那么需要几次找到呢？看下面的运行结果

可以看出经历了六次循环调用才找到；如果我们找value=50,那么一次就能成功！所以这个调用多少次与mid的取值也有很大关系；

分析mid=(begin+end)/2，看出begin、end无法做出改变，那么只有对1/2进行改动；mid=(begin+end) / {(value-arr[begin])/(arr[end]-arr[begin])}，根据上文中找寻1，我们可以算出mid = 1，所以一步就能找到；这就是下文提到的插值查找

---

🚢 插值查找算法

根据上文进行分析，这个插值查找算法是对二分查找算法的改进。
mid=(begin+end) / {(value-arr[begin]) / (arr[end]-arr[begin])}

☸下面这段源代码除了mid求的不一样之外，其他一模一样。☸

/**
     * 自适应求出mid
     * @param arr 待搜索数组
     * @param value 待查询的值
     * @param begin 左索引
     * @param end   右索引
     * @param list  存储搜索值下表的集合
     */
    private static void interpolationSearch(int[] arr, int value, int begin, int end, List<Integer> list) {
    	System.out.println("test");
        //这个value要进行判断是否小于arr[0]，否者在下面求mid时会报错
        if (begin > value || value < arr[0] || value > arr.length - 1) {
            return;
        }
        int mid = (begin + end) * (value - arr[begin]) / (arr[end] - arr[begin]);
        if (value > arr[mid]) {
            interpolationSearch(arr, value, mid + 1, end, list);
        } else if (value < arr[mid]) {
            interpolationSearch(arr, value, begin, mid - 1, list);
        } else if (value == arr[mid]) {
            int tempFront = mid - 1;
            while (true) {
                if (tempFront < 0 || value != arr[tempFront]) {
                    break;
                }
                list.add(tempFront);
                tempFront--;
            }
            list.add(mid);
            int tempAfter = mid + 1;
            while (true) {
                if (tempAfter > end || value != arr[tempAfter]) {
                    break;
                }
                list.add(tempAfter);
                tempAfter++;
            }
        }
    }

根据数组为arr[1,2,3,4,5…,98,99,100] ，查找其中的1，只需一次便能查到.

---

🚢 斐波那契查找算法

…