论文阅读生成模型——变分自编码器(Variational Auto-Encoder，VAE)

Posted 2021-10-14 Paul-Huang

1. VAE设计思路：从PCA到VAE

VAE最想解决的问题是如何构造编码器和解码器，使得图片能够编码成易于表示的形态，并且这一形态能够尽可能无损地解码回原真实图像。

1.1 PCA

这似乎听起来与PCA（主成分分析）有些相似，而PCA本身是用来做矩阵降维的：

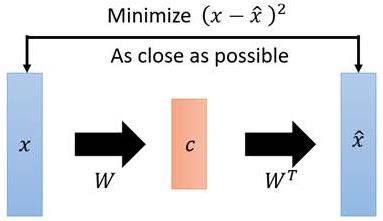
如图：

• $X$本身是一个矩阵，通过一个变换$W$变成了一个低维矩阵$c$；
• 因为这一过程是线性的，所以再通过一个$\hat{W}$变换就能还原出一个$\hat{X}$；
• 现在找到一种变换$W$，使得矩阵$X$与能够尽可能地一致，这就是PCA做的事情。

在PCA中找这个变换$W$用到的方法是$SVD（奇异值分解）算法$，在VAE/AE中不再需要使用SVD，直接用神经网络代替。

1.2 自编码器(Auto-Encoder, AE)

• PCA与想要构造的自编码器(AE)的相似之处是：如果把矩阵$X$视作输入图像，$W$视作一个编码器，低维矩阵$c$视作图像的编码，然后$\hat{W}$和$\hat{X}$分别视作解码器和生成图像，PCA就变成了一个自编码器(AE)网络模型的雏形。
  
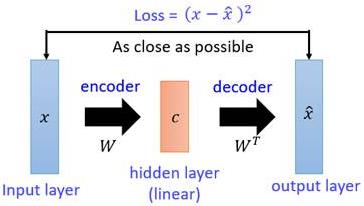
• 对这一雏形进行改进。用神经网络代替$W$变换和$\hat{W}$变换，就得到了如下Deep Auto-Encoder模型：
  

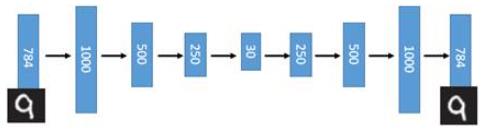
  引入了神经网络强大的拟合能力，使得编码（Code）的维度能够比原始图像（$X$）的维度低非常多。在一个手写数字图像的生成模型中，Deep Auto-Encoder能够把一个784维的向量（28*28图像）压缩到只有30维，并且解码回的图像具备清楚的辨认度（如下图）。
  

1.3 从AE到VAE

• AE的缺陷
  对于一个生成模型而言，解码器部分应该是单独能够提取出来的，并且对于在规定维度下$任意采样的一个编码，都应该能通过解码器产生一张清晰且真实的图片$。如下图，AE模型无法实现：
  
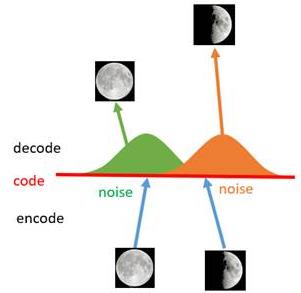
  如上图所示，假设有两张训练图片，一张是全月图，一张是半月图，经过训练我们的自编码器模型已经能无损地还原这两张图片。接下来，我们在code空间上，两张图片的编码点中间处取一点，然后将这一点交给解码器，我们希望新的生成图片是一张清晰的图片（类似3/4全月的样子）。但是，实际的结果是，生成图片是模糊且无法辨认的乱码图。

  一个比较合理的解释是，因为编码和解码的过程使用了深度神经网络，这是一个非线性的变换过程，所以$在code空间上点与点之间的迁移是非常没有规律$。

• VAE的引入
  如何解决上述问题呢？我们引入噪声，使得图片的编码区域得到扩大，从而掩盖掉失真的空白编码点。
  
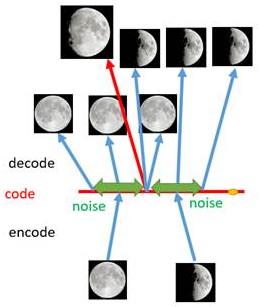
  1. 如上图所示，给两张图片编码的时候加上一点噪音，使得每张图片的编码点出现在$绿色箭头$所示范围内，于是在训练模型的时候，绿色箭头范围内的点都有可能被采样到，这样解码器在训练时会把绿色范围内的点都尽可能还原成和原图相似的图片。
  2. 之前关注的失真点，现在它处于全月图和半月图编码的交界上，于是解码器希望它既要尽量相似于全月图，又要尽量相似于半月图，于是它的还原结果就是两种图的折中（3/4全月图）。
  3. 给编码器增添一些噪音，可以有效覆盖失真区域。不过这还并不充分，因为在上图的距离训练区域很远的$黄色点处$，它依然不会被覆盖到，仍是个失真点。
  4. 为了解决上述问题，试图把噪音无限拉长，使得对于每一个样本，它的编码会$覆盖整个编码空间$，不过我们得保证，在$原编码附近编码的概率最高，离原编码点越远，编码概率越低$。在这种情况下，图像的编码就由原先离散的编码点变成了一条$连续的编码分布曲线$，如下图所示。
     
     上述的这种$将图像编码由离散变为连续的方法$，就是$变分自编码的核心思想$。

降维方法	线性	非线性
生成式	概率PCA	VAE
非生成式	PCA	AE

---

2. VAE模型框架

2.1 问题描述

1. 情况介绍
   观测数据集$X={\left\{{\mathtt{x}}^{(i)}\right\}}_{i=1}^{N}i.i.d$（$X$本身可能是连续分布或者离散分布），假设 $X$由隐变量$\mathtt{z}$(unobserved continuous random variable)生成。此过程包含2个步骤：

   • $先验分布p_{{\theta }^{\ast }}(\mathtt{z})生成一个{\mathtt{z}}^{(i)}$;
   • $条件分布p_{{\theta }^{\ast }}(\mathtt{x}|\mathtt{z})生成一个{\mathtt{x}}^{(i)}$。

   假设$p_{{\theta }^{\ast }}(\mathtt{z}),p_{{\theta }^{\ast }}(\mathtt{x}|\mathtt{z})$来自$p_{{\theta }^{\ast }}(\mathtt{z}),p_{{\theta }^{\ast }}(\mathtt{x}|\mathtt{z})$函数族，并且它们的概率密度函数（PDF）几乎在$\theta$和$z$的任何地方都是可微的。这个过程中$真正的参数{\theta }^{\ast }$和$隐变量z^{(i)}$的值都是$未知的$。

2. 存在问题

   • 难处理性：
     边际似然函数的积分$p_{\theta }(\mathtt{x})={\int }_{}^{}{p}_{\theta }(\mathtt{z})p_{\theta }(\mathtt{x}|\mathtt{z})dz$难以计算（没办法估计边际似然分布，因为其中的后验分布 p θ ( z ∣ x ) = p θ ( x ∣ z ) p θ ( z ) p θ ( x ) \\color{blue}p_{\\theta}(\\mathtt{z|x})=\\frac{p_{\\theta}(\\mathtt{x|z})p_{\\theta}(\\mathtt{z})}{p_{\\theta}(\\mathtt{x})} 变分自编码器背后的直觉VAE

     一文搞懂变分自编码器(VAE, CVAE)

     自编码器，变分自编码器和生成对抗网络异同

     变分自编码器的原理与项目实战

     变分自编码器的原理与项目实战

     变分自编码器：原来是这么一回事