论文阅读|《Bi-level Actor-Critic for Multi-agent Coordination》(AAAI 2020)（附带源码链接）

Posted 2021-10-14 码丽莲梦露

源码链接：GitHub - laonahongchen/Bilevel-Optimization-in-Coordination-Game: code implementation for 'Bi-level Actor-Critic for Multi-agent Coordination'(AAAI2020)

1 摘要

        协调是多智能体系统的基本问题之一。典型的多智能体强化学习(MARL)方法对智能体一视同仁，其目标是在存在多重均衡时将马尔可夫博弈求解到任意的纳什均衡(NE)，从而缺乏解决NE选择的方法。在本文中，我们平等地对待Agent，并认为Stackelberg均衡在帕累托优势方面是一个比Nash均衡更好的收敛点，特别是在合作环境中。在马尔可夫对策下，我们正式定义了寻找Stackelberg均衡的双层强化学习问题。我们提出了一种新颖的双层Actor-Critic学习方法，该方法允许Agent拥有不同的知识库(因此是智能的)，同时他们的动作仍然可以同时和分布式地执行。给出了算法的收敛性证明，并针对现有的学习算法进行了测试。我们发现，所提出的双层Actor-Critic算法成功地收敛到矩阵博弈中的Stackelberg均衡，并在高速公路合并环境中找到了一个非对称解。

2 介绍

        在博弈论中，协调博弈被定义为具有多个纳什均衡的博弈。博弈论文献中提出了纳什均衡选择的各种标准，如显著性和公平性，其中，在应用这些标准之前，假设代理知道博弈模型。针对智能体不知道博弈模型但可以通过与环境交互来学习博弈模型的环境，提出了多智能体强化学习方法来寻找纳什均衡，包括纳什Q学习、MADDPG以及Mean-Field Q-learning.这些model-free的方法集中训练代理收敛到纳什均衡，然后分布式执行代理。然而，这些方法不能保证特定的收敛纳什均衡，从而导致不确定性和次最优性。

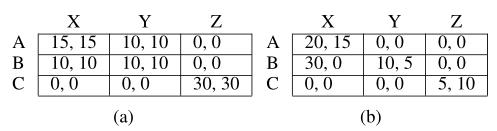
        为了解决这个问题，我们从一个不对称的角度重新考虑了协调问题。虽然原始博弈模型是对称的，即Agent同时决策，但我们仍然能够在训练阶段为Agent定义决策优先级，并在执行阶段保持同步决策。在这个非对称博弈模型中，学习目标自然是Stackelberg均衡(SE)，而不是纳什均衡(NE)。SE优化领导者的策略，因为跟随者总是扮演最佳响应策略。尽管SE对追随者有歧视，但我们惊讶地发现，在广泛的环境中，SE比NE更优越。例如，在合作博弈中，SE被保证是帕累托最优的，而只有一个NE实现了这一点，如表1a所示。在表1b所示的非合作情况下，SE不包括在NE集合中，并且其帕累托优于任何NE。总体而言，我们的实证研究表明，在合作水平较高的博弈中，自主性很可能优于平均自主性。

3 Bi-level Optimization

        本文假设两参与人马尔可夫对策中的代理是不对称的，即后面的代理观察前面的代理的行为，从而解决了马尔可夫对策的一个双层优化问题。原双层优化问题的表达式为:

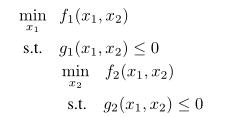
         双层优化问题可以等价地描述为一个Stackelberg博弈，上层优化器为leader，下层优化器为fellower，双层优化问题的解为Stackelberg均衡。

 4 Bi-level Reinforcement Learning

 4.1 Problem Formulation

        将Bi-level optimization与Markov博弈联系起来，假设Agent 1为leader, Agent 2为follower，我们的问题表示为:

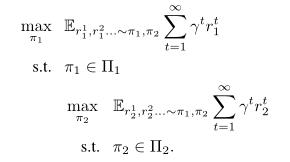
        我们把这个问题叫做双层强化学习(BiRL)。BiRL可以看作是Stackelberg博弈的多状态版本，并将标准的双层优化问题扩展到两个维度:1)目标是序列状态下的折扣报酬的总和;2)目标函数的形式是未知的，只能通过与环境的交互以无模型的方式学习。

 4.2 Stackelberg Equilibrium vs. Nash equilibrium

        协同博弈一个具有多个纳什均衡的博弈，其协调问题可以看作是一个纳什均衡选择问题。在本文中，我们考虑Stackelberg均衡作为协调对策的潜在较好解。下图是一个例子，说明了NE和SE在马尔可夫博弈中的区别。

        下图博弈可看作一个关于BiRL的合作游戏例子。Agent A和Agent B在网格中同时移动，只有当他们都在10或20方格时才能获得共同奖励。联合策略使两个agent达到10或20是纳什均衡，只有联合策略使两个agent达到20是Stackelberg均衡，是BiRL的解。

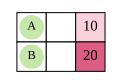
        SE的第一个优势是确定性或独特性。一个游戏中可能存在多个NEs，而多个se只能在非常严格的条件下存在。

        SE的第二个优点是性能。在协调环境中，SE比平均NE具有更好的帕累托优势。一个极端的例子是合作游戏。在合作博弈中，SE总是达到帕累托最优点，而只有最佳NE达到帕累托最优.

         为了证明此观点，我们将二人马尔可夫博弈的合作水平正式定义为agent的累积报酬之间的相关性:

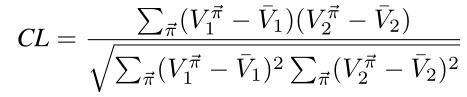
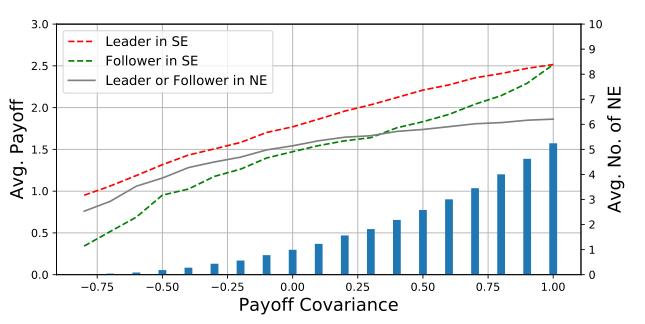
         从上图的结果可以看出，无论是在完全合作的博弈中，还是在合作程度高的博弈中，领导者和follower在SE中都获得了更高的收益。我们还发现博弈中纳什均衡的个数与合作水平正相关，说明合作水平高的博弈更容易出现协调问题。因此，我们认为，在协调问题中，特别是在高度合作的博弈中，SE通常比平均NE具有帕累托优势。

 4.3 Bi-level Tabular Q-learning

         类似于minimax-Q和Nash-Q，我们可以通过指定计算方法来定义最优状态值的双层Bellman方程：

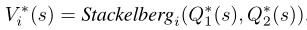
         基于贝尔曼方程，Q1和Q2的更新规则设计如下：

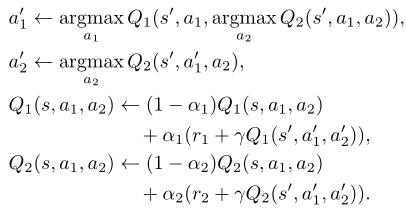
4.3 Bi-level Actor-Critic

         随着问题复杂度更高，bi-level Q-learning methods 将扩展到Multi-level,动作空间将呈指数增长。

       为了解决这一问题，我们提出了双层Actor-Critic(Bi-AC)方法，该方法为fellower引入一个Actor，同时保持learder作为Q-learner。形式上，设π2(s, a1;φ2)∈PD(A2)表示agent 2的策略模型(或actor)，该模型在输入agent 1当前状态的基础上，再以agent 1的动作作为输入。我们还使用两个agent的近似函数对两个Critic建模。我们有以下更新规则，给定<s,a1,a2,s',r1,r2>学习率αi， β:

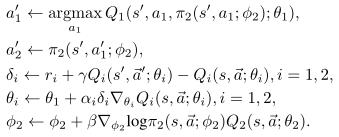
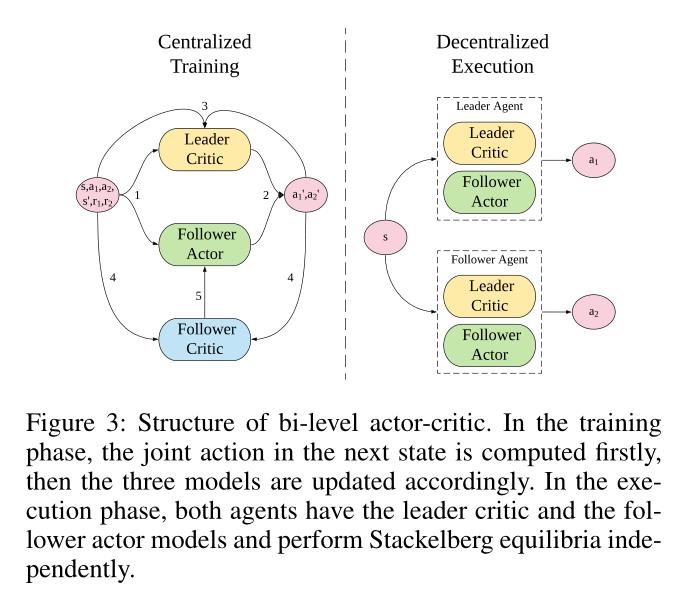
        Bi-AC可以自然地扩展n-level Actor-Critic。在连续行动空间的情况下，我们定义确定性策略模型:

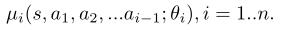
         我们还将每个agent的Q函数建模为:

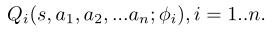
         在每个训练步骤中，由上层agent向下层agent逐个确定下一步的动作，并对模型进行相应的更新:

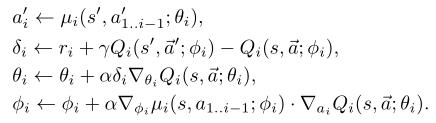
5 Convergence and Limitation 

 在以下假设下，Bi-AC将收敛到Stackelberg均衡:

        (1)对于所有的t和s，每个阶段博弈(Qt1(s)， Qt2(s))都有一个全局最优点，actor函数选择这一点上的agent的收益，以概率1更新critic函数。

        (2)

        

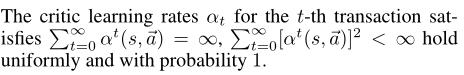
        (3)所有博弈的每个阶段博弈(Qt1(s)， Qt2(s))都是全局最优点，Bi-AC选择这一点上的agent的收益，以概率1更新评判函数。

        上面的假设3是一个强假设，即使在训练过程的一开始可能也不能满足。然而，如实验部分后面所示，我们的算法在很多情况下是收敛的。