剑指 Offer 11. 旋转数组的最小数字

Posted 2023-03-05 庄小焱

摘要

剑指 Offer 11. 旋转数组的最小数字

153. 寻找旋转排序数组中的最小值

154. 寻找旋转排序数组中的最小值 II

一、二分查找

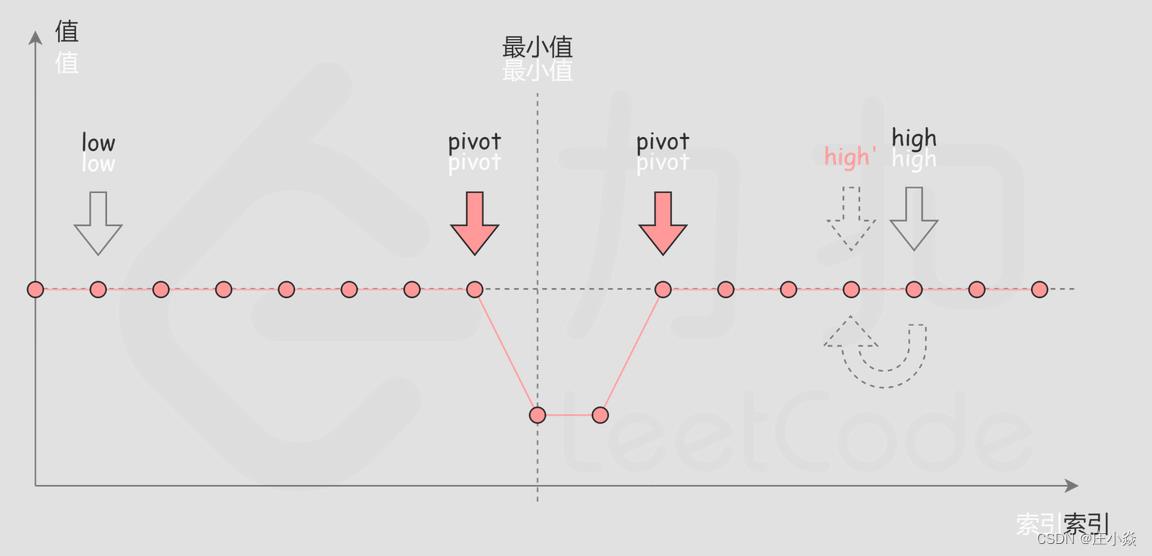
一个包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：

我们考虑数组中的最后一个元素x：在最小值右侧的元素，它们的值一定都小于等于x；而在最小值左侧的元素，它们的值一定都大于等于x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为low，右边界为high，区间的中点为pivot，最小值就在该区间内。我们将中轴元素numbers[pivot]与右边界元素 numbers[high]进行比较，可能会有以下的三种情况：

• 第一种情况是 numbers[pivot]<numbers[high]。如下图所示，这说明 numbers[pivot]是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

• 第二种情况是 numbers[pivot]>numbers[high]。如下图所示，这说明 numbers[pivot]是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

第三种情况是numbers[pivot]==numbers[high]。如下图所示，由于重复元素的存在，我们并不能确定numbers[pivot]究竟在最小值的左侧还是右侧，因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是，由于它们的值相同，所以无论 numbers[high]是不是最小值，都有一个它的替代品numbers[pivot]，因此我们可以忽略二分查找区间的右端点。

class Solution 
    public int minArray(int[] numbers) 
        int low = 0;
        int high = numbers.length - 1;
        while (low < high) 
            int pivot = (high +low)>> 1;
            if (numbers[pivot] < numbers[high]) 
                high = pivot;
             else if (numbers[pivot] > numbers[high]) 
                low = pivot + 1;
             else 
                high -= 1;
            
        
        return numbers[low];
    

复杂度分析

• 时间复杂度：平均时间复杂度为 O(log⁡n)，其中n是数组numbers的长度。如果数组是随机生成的，那么数组中包含相同元素的概率很低，在二分查找的过程中，大部分情况都会忽略一半的区间。而在最坏情况下，如果数组中的元素完全相同，那么while循环就需要执行n次，每次忽略区间的右端点，时间复杂度为O(n)。
• 空间复杂度：O(1)。

二、模拟解析

    public int minArray2(int[] numbers) 
        if (numbers.length < 2) 
            return numbers[0];
        
        int res = numbers[0];
        for (int i = 0; i < numbers.length - 1; i++) 
            if (numbers[i] > numbers[i + 1]) 
                res = numbers[i + 1];
                break;
            

        
        return res;
    

复杂度分析

• 时间复杂度：平均时间复杂度为 O(⁡n)，其中n是数组numbers的长度。
• 空间复杂度：O(1)。

博文参考

《leetcode》