论文翻译DeepWalk: Online Learning of Social Representations
Posted 奇跡の山
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文翻译DeepWalk: Online Learning of Social Representations相关的知识,希望对你有一定的参考价值。
背景介绍
这几年图神经网络模型(如谱聚类的GCN、GAT等等)都挺火的,这些图神经网络即将节点或图映射到一个低维空间(称为图嵌入);而除了GNN还有很多图嵌入方法(在GNN之前图嵌入的概念常出现在流行学习和网络分析的研究中),这类图嵌入方法可以分为【基于矩阵分解的图嵌入方法】和【基于随机游走的图嵌入方法】,后者方法就是来自本篇论文,即第一个将NLP的思想用在网络嵌入(Networking Embedding,NE)的。

论文:《DeepWalk: Online Learning of Social Representations》
论文作者:B. Perozzi, R. Al-Rfou, and S. Skiena
论文来源:KDD, 2014
论文链接:https://arxiv.org/abs/1403.6652
发在KDD上的最终版本:https://dl.acm.org/doi/10.1145/2623330.2623732
github链接:https://github.com/phanein/deepwalk
文章目录
零、Abstract
本文提出DeepWalk算法——一种用于学习网络中顶点的潜在表示的新方法,这些潜在表示将社会关系编码到连续的向量空间中,以至于能容易地用到统计模型中。DeepWalk将语言建模和无监督特征学习(或深度学习)的最近进展,从单词序列推广到图中。
DeepWalk将随机游走得到的节点序列作为句子,从截断的随机游走序列中得到网络的局部信息,通过这些局部信息来学习节点的潜在表示。为了证实DeepWalk得到的节点的潜在表示的效果,本文对几个社交网络(如BlogCatalog,Flickr和YouTuBe等)进行了多标签分类任务。我们的结果显示,DeepWalk算法能够对网络进行全局的观察,特别是在缺失信息的情况下,也能比baselines强。当标记数据稀疏(很少)时,DeepWalk的表示得到的F1分数比同类方法高出10%。在一些实验中,当训练数据少于60%时,DeepWalk算法能够胜过所有对比算法。
DeepWalk也是可扩展的,它是一种可以建立有用的增量(incremental)结果的在线学习算法,而且是平行的。这些特性使其适用于广泛的实际应用,如网络分类和异常检测。
一、Introduction
首先介绍了网络嵌入是什么,以社交网络为例,网络嵌入是将网络中的点用一个低维的向量表示(这些向量要能反应原网络的某些特性,比如如果在原网络中两个点的结构相似,则两个点表示成的向量也应该类似)。
过去:普通的邻接矩阵当存储很多关系时,维度将变得很高,而矩阵分解非常费时且复杂,所以通过矩阵分解的方法进行网络的表示学习,目前没有应用在大规模数据集的方案中。
在NLP任务中,word2vec是一种常用的word embedding方法,它通过语料库的句子序列来描述词与词之间的共现关系,进而学习词语的向量表示。
本文是第一次引入深度学习的无监督特征学习,通过将NLP模型word2vec应用到网络的表示上,做到了无需进行矩阵分解即可表示出网络中的节点的关系。文中提出了一种网络嵌入的方法DeepWalk——它的输入是一张图或网络,输出是网络中顶点的潜在向量表示(将社交关系编码成维度较小的连续向量空间)。下图是将DeepWalk用于学习好的Karate网络的效果,我们
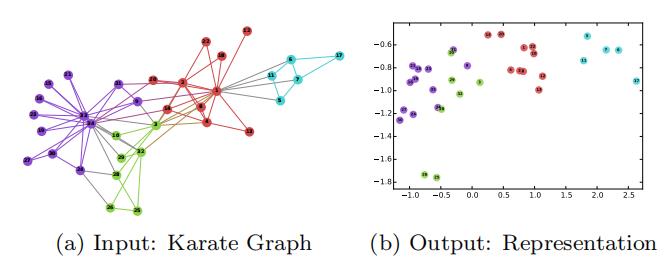
DeepWalk通过一串截断随机游走(truncated random walk)类似word2vec中对单词的上下文,作为word2vec算法的输入,进而把节点表示成向量,从而学习出一个网络的社交表示(social representation),在网络标注顶点很少的情况也能得到较好效果。输出的结果能被作为多种分类算法作为输入应用。该算法具有可扩展性的有点,能够适应网络的变化。
- DeepWalk思想类似word2vec,使用图中节点之间的共现关系来学习节点的向量表示。那么问题关键就是如何描述节点之间的共现关系——DeepWalk的方法是使用随机游走(Random Walk)的方式在图中进行节点采样。
- Random Walk是一种可重复访问已访问节点的DFS算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复该过程,直到访问序列长度满足预设要求。
本文的三点主要贡献有:
- 使用深度学习去分析图,建立了一个适合统计建模的健壮表征方法。DeepWalk根据短距离的随机游走学习结构化表示。
- 在社会网络的多标签分类任务上评估我们的表征方法,显示:在标签的出现次数稀疏情况下,算法在指标Micro F1值上提高了5%-10%;在一些栗子上,即使提取40%的训练数据,DeepWalk算法的representations仍然能获得很好的效果。
- 作者通过采用并行的方法构建web-scale graphs(例如youtube)的representations表明了算法的可扩展性。
二、Problem Definition
将社交网络的成员分类问题考虑为一个或多个类别。
- 给定部分标记的社交网络 G L = ( V , E , X , Y ) G_L=(V,E,X,Y) GL=(V,E,X,Y) 的形式表示,其中属性 X ∈ R ∣ V ∣ × S X \\in \\mathbb{R}^{|V| \\times S} X∈R∣V∣×S ( S S S是每个属性向量的特征空间的大小)。
- Y ∈ R ∣ V ∣ × ∣ Y ∣ Y \\in \\mathbb{R}^{|V| \\times |Y|} Y∈R∣V∣×∣Y∣ 。 Y Y Y是标签集,是一个节点个数x标签个数的矩阵,代表每个节点都有一个自己的标签。
任务是将社交网络中的结点进行分类,但该分类问题和普通分类不同。在传统的机器学习分类设置中,目标是学习一个假设
H
H
H,它将
X
X
X的元素映射到标签集
Y
Y
Y。
但对于一个图,需要利用到节点在图中嵌入的信息,即节点邻居等。这部分信息常常是隐藏的,不体现在
X
X
X当中,需要结合网络结构来进行分类[37],单个节点的分类不是独立的任务,而是与其它节点的分类相关。这被称作集体分类(Collective Classification)或关联分类(Relational Classification)。
DeepWalk从关联分类任务中提取除了上游子任务——学习所有结点的嵌入表示 X E ∈ R ∣ V ∣ × d X_E \\in \\mathbb{R}^{|V| \\times d} XE∈R∣V∣×d,其中 d d d是一个较小的维度数, X E X_E XE可用于捕捉节点的结构信息。
三、Learning Social Representions
学习一个网络表示时需要注意的几个性质:
- 适应性。网络表示需要适应网络的变化(不断会有新节点和边添加进来)。
- 社群性。网络中往往会出现一些特征相似的点构成的团状结构,这些节点表示成向量后必须相似。
- 低维性。低维度的表示可以在少量标注数据上获得更好的泛化性能,过高会有过拟合的风险,对网络中有缺失数据的情况处理能力较差。
- 连续性。低维的向量应该是连续的。连续的表示在区分社区边界上更加平滑,使得分类结果更加鲁棒。
网络嵌入和NLP的word2vec即词嵌入类似,前者是将网络节点用向量表示,后者是将单词用向量表示。
3.1 Random Walks
随机游走(random walk),在网络上不断重复随机选择游走路径,最终形成一条贯穿网络的路径。从某个特定的端点开始,每次从当前节点相连的边中随机选择一条,沿着选定的边移动到下一个顶点,不断重复该过程。阶段随机游走(truncated random walk)实际是长度固定的随机游走。
随机游走的两个好处:
- 并行性:随机游走是局部行为,在大网络中,可以同时在不同的点开始截断随机游走,从而减少采样的时间。
- 适应性:适应网络的局部变化,因为网络的演化(如局部的点和边的变化)对只会部分的随机游走路径产生影响,因此在网络的演化过程中不需要每一次都重新计算整个网络的随机游走。
3.2 Connection:Power laws(连接:幂律)
自然语言已被证明是符合幂次定律,只要证明图的数据的也符合幂次定律就可以对图的表示应用对自然语言表示的方法。下图比较了对图进行短随机游走中向量出现的频率与单词在文本信息中出现的频率。可见对图的短随机游走也是大致满足幂次定律的:

3.3 Language Modeling
语言模型主要是学词序列:
W
1
n
=
(
w
0
,
w
1
,
⋯
,
w
n
)
W_{1}^{n}=\\left(w_{0}, w_{1},\\cdots, w_{n}\\right)
W1n=(w0,w1,⋯,wn)我们需要用前n个单词预测第n个单词,即将
Pr
(
w
n
∣
w
0
,
w
1
,
⋯
,
w
n
−
1
)
\\operatorname{Pr}\\left(w_{n} \\mid w_{0},w{1},\\cdots,w_{n-1}\\right)
Pr(wn∣w0,w1,⋯,wn−1)但是论文的目的是要学习一个隐表示,因此引入一个映射函数:
Φ
:
v
∈
V
↦
R
∣
V
∣
×
d
\\Phi: v \\in V \\mapsto \\mathbb{R}^{|V| \\times d}
Φ:v∈V↦R∣V∣×d,所以问题就变成了估计
Pr
(
v
n
∣
Φ
(
v
0
)
,
Φ
(
v
1
)
,
⋯
,
Φ
(
v
n
−
1
)
)
\\operatorname{Pr}\\left(v_{n} \\mid \\Phi\\left(v_{0}\\right), \\Phi\\left(v_{1}\\right), \\cdots, \\Phi\\left(v_{n-1}\\right)\\right)
Pr(vn∣Φ(v0),Φ(v1),⋯,Φ(vn−1))但是如果随机游走的长度变大,会降低该条件概率估计的效率,NLP中针对这个问题给出以下几个方案:
(1)将上下文预测一个单词的问题,转为根据一个单词预测上下文的问题;
(2)在一个给定单词的左边和右边都会出现上下文内容
(3)去掉单词出现的顺序约束
于是问题变成了如下最优化问题。因为顺序被忽略了,所以比较适合图学习。
minimize
Φ
−
log
Pr
(
{
v
i
−
w
,
⋯
,
v
i
−
1
,
v
i
+
1
,
⋯
,
v
i
+
w
}
∣
Φ
(
v
i
)
)
\\underset{\\Phi}{\\operatorname{minimize}}-\\log \\operatorname{Pr}\\left(\\left\\{v_{i-w}, \\cdots, v_{i-1}, v_{i+1}, \\cdots, v_{i+w}\\right\\} \\mid \\Phi\\left(v_{i}\\right)\\right)
Φminimize−logPr({vi−w,⋯,vi−1,vi+1,⋯,vi+w}∣Φ(vi))
四、Method
4.1 Overview
4.2 Algorithm:DeepWalk
算法由两部分组成:(1)随机游走序列生成器;(2)向量更新。
随机游走:对图G均匀地随机采样一个节点
v
i
v_i
vi,并作为random walk的根结点
W
v
i
W_{v_{i}}
Wvi,然后一直向周围邻居采样,直到达到最大路径长度
t
t
t。
随机游走的长度没有限制,但是在实验中设置最大步长是固定的。

- 输出:一个顶点表示矩阵 Φ \\Phi Φ,大小为 ∣ V ∣ × d |V|\\times d ∣V∣×d
- 第二行:构建Hierarchical Softmax
- 第三行:对每个节点做 γ \\gamma γ次随机游走
- 第四行:打乱网络中的节点
- 第五行:以每个节点为根结点生成长度为 t t t的随机游走
- 第七行:根据生成的随机游走使用skip-gram模型利用梯度的方法对参数进行更新。
其中SkipGram参数更新的细节如下:

(1)SkipGram
SkipGram参数更新的细节如下:

SkipGram算法是语言模型中,最大化窗口
w
w
w中出现的词的概率的方法(梯度下降),外层for循环是对这个序列中的每个词进行操作,内层for循环是对每个词的窗口大小为
w
w
w的词序列进行操作。具体操作是用一个似然函数
J
(
Φ
)
J(\\Phi)
J(Φ)表示
Φ
\\Phi
Φ,通过梯度下降(对
J
(
Φ
)
J(\\Phi)
J(Φ)求导)更新参数(
α
\\alpha
α是学习速率)。
从词向量学习的角度看,基于神经网络语言模型的预训练方法存在缺点:当对t时刻词进行预测时,模型只利用了历史词序列作为输入,而损失了与“未来”上下文之间的共现信息。于是大佬们提出更强的词向量预训练模型Word2Vec,其中包括CBOW(Continuous Bag-of-Words)模型以及Skip-gram模型。
(2)Hierarchical Softmax
以上是关于论文翻译DeepWalk: Online Learning of Social Representations的主要内容,如果未能解决你的问题,请参考以下文章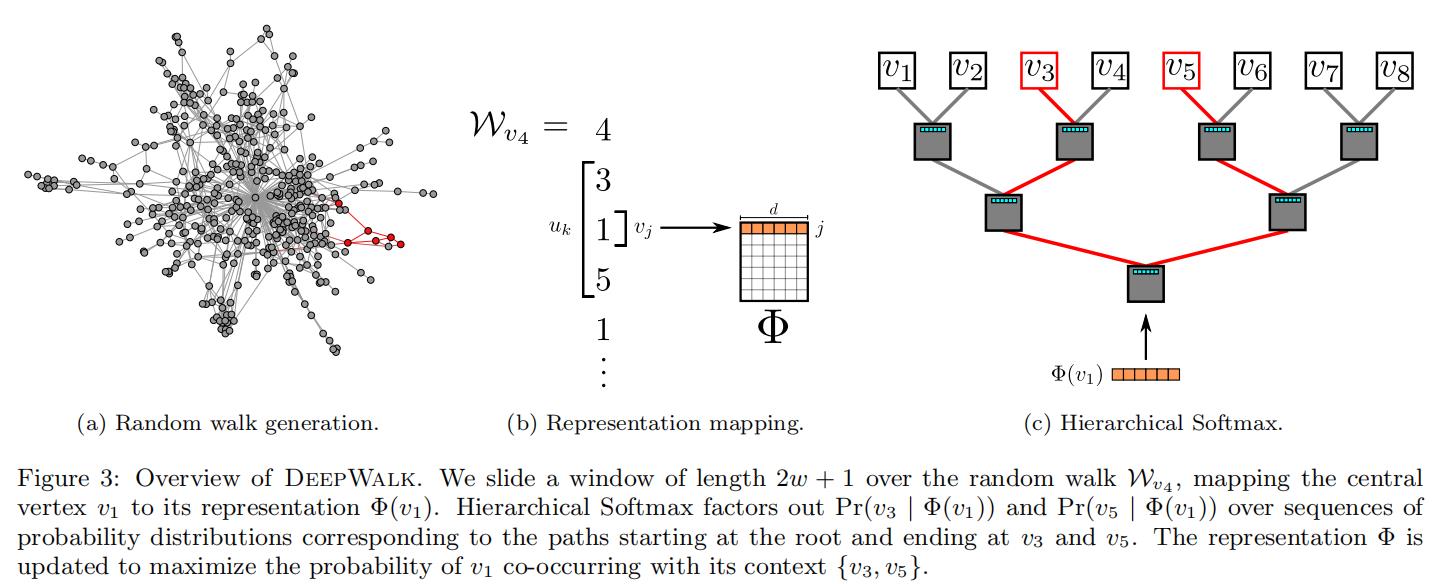
在计算
Pr
(
u
k
∣
Φ
(
v
i
)
)
\\Pr(u_k|\\Phi(v_i))
Pr(uk∣Φ(vi)) 时,可以利用Hierarchical Softmax二叉树[29, 30]加速。作者将所有节点作为二叉树的叶子节点,就可以用从根节点到叶子节点的路径来表示每个节点。二叉树若有
∣
V
∣
|V|
∣V∣个叶子节点,则深度至多为
log
∣
V
∣
\\log|V|
log∣V∣。这样就会有:
Pr