2021icpc网络赛A题ac代码及思路

Posted 2021-10-13 算法与编程之美

本文首发于微信公众号："算法与编程之美"，欢迎关注，及时了解更多此系列文章。

思路

读完题后了解题的大意：有k个节点，编号为0 - k-1，每个节点可以在空闲时间处理请求，每个请求的有一个到达时间和处理该请求的持续时间；节点空闲表示当一个请求在达到时间时，该节点未处理任何一个其他请求，即为该节点空闲！第i个请求优先考虑i % k 个节点是否为空，不为空优先考虑i % k, 否则依次后推，(1 + 1) % k, (i + 2) % k，直到找到空闲节点为止。

然后我看了一下数据大小k个节点和n组请求 k, n <= 1^5；以及节点的到达时间和持续时间 <= 1e9; 所以本题涉及的最大数据不会超过2e9！，不会报int；最开始模拟去写，然后tle了，因为最坏的情况时n*k,我们需要将其控制在nlog(k) 以内；

模拟思路1

模拟思路就是去模拟这个过程，优先考虑i%k是否满足，不满足继续后推(i + 1) % k … 如果所有的节点都不满足当前时间为空闲就表示第i个请求不被接收；然而最坏的情况就是每次都没有满足的节点，我们都要去模拟一次整个过程也就是所有节点，单次模拟时间复杂度就是k, 那么n次时间复杂度就是n*k; n, k <= 1^5, 所以最坏情况必定会tle.

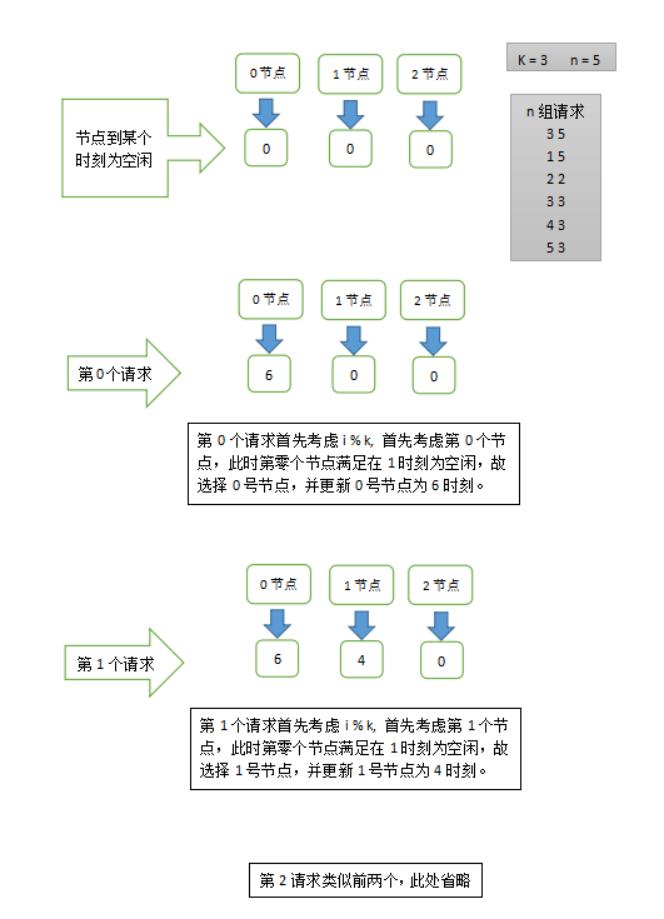
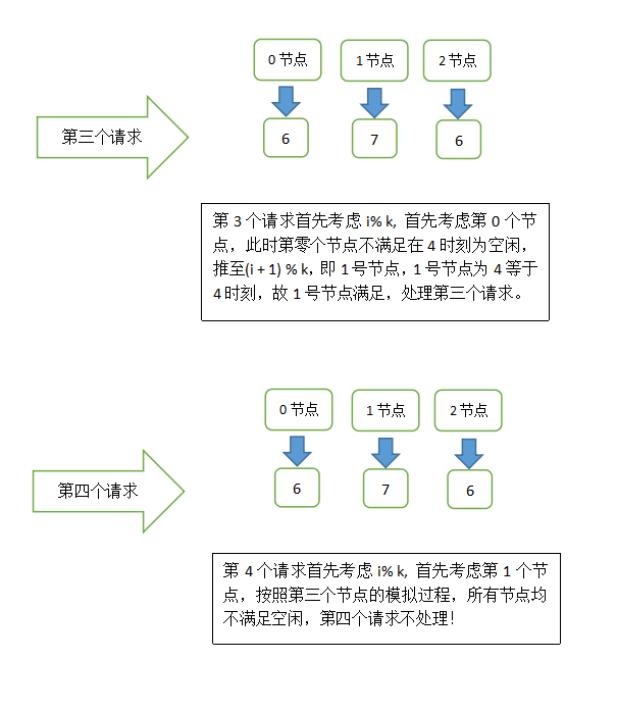 模拟过程，节点1处理了两个请求， 0，2节点各一个，故此1处理请求最多，输出1.

线段树优化思路

我们唯一能优化的地方就是单次查找的节点，单次查找满足条件的节点采用线段树去优化，可以将其每次查找的复杂度降低到log(k)级别；线段树优化：线段树优化需要维护一个区间内的最小值(也就是某个节点在最小的时间段空闲)，如果该最小值小于某个请求的到来时间，代表该区间存在一个满足条件的节点能够处理到来的请求；因为考虑道第i个请求的优先选择i%k 节点， 所以我们ask操作时， 区间分别为 (i%k+1 ~ k) 就是i%k的右半部分区间优先考虑，其次左半部分的区间(1 ~ i%k) (注：因为此处是从1 - k，所以i % k应该再加一个1)；

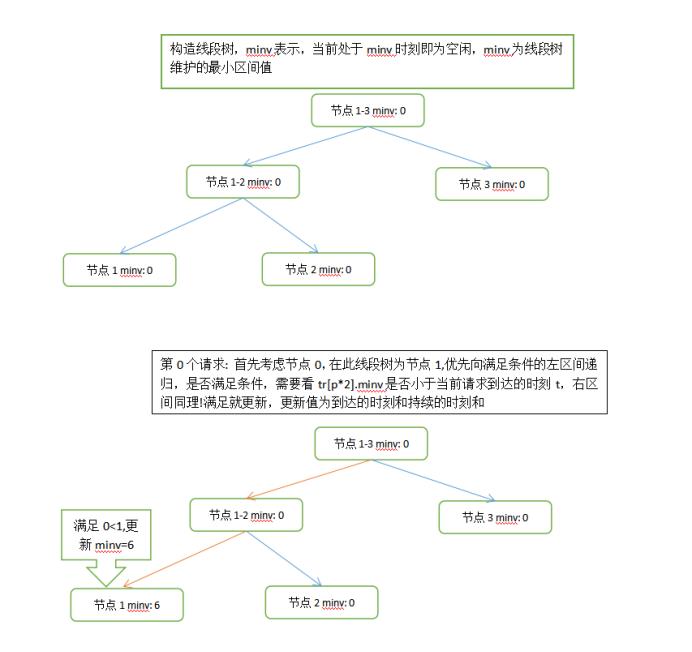
 依次内推，写出线段树板子即可！

#include <iostream> #include <algorithm> #include <cstring> #include <string> #include <queue> #include <vector> #include <cstdio> using namespace std; typedef long long LL; const int N = 100010, INF = 2e9+10; LL a[N], n, k; LL cnt[N]; struct SegmT{     LL l, r;     LL val; } tr[N * 4]; void upside(int p){     tr[p].val = min(tr[p * 2].val, tr[p * 2 + 1].val); } void build(LL p, LL l, LL r){     tr[p].l = l, tr[p].r = r;     if (l == r) {         tr[p].val = 0;         return;     }     LL mid = (l + r) >> 1;     build(p * 2, l, mid);     build(p * 2 + 1, mid + 1, r);     upside(p); } void change(LL p, LL x, LL v){     if (tr[p].l == tr[p].r){         tr[p].val = v;         return;     }     LL mid = (tr[p].l + tr[p].r) >> 1;     if (x <= mid) change(p * 2, x, v);     else change(p * 2 + 1, x, v);     upside(p); } LL ask(LL p, LL l, LL r, LL t){     if (tr[p].l == tr[p].r) {         return tr[p].r;     }     LL mid = (tr[p].l + tr[p].r) >> 1;     LL res = -1;     if (l <= mid && r >= tr[p].l && tr[p * 2].val <= t){         res = ask(p * 2, l, r, t);     }     if( res == - 1 && r >= mid + 1 &&  l <= tr[p].r && tr[p * 2 + 1].val <= t){         res = ask(p * 2 + 1, l, r, t);     }     return res; } int main(){     cin >> k >> n;     for (int i = 0; i < N * 4; i ++) tr[i].val = INF;     build(1, 1, k);     LL res = 0;     for (int i = 0; i < n; i ++){         LL co, t;         scanf("%lld %lld", &co, &t);         LL p = (i % k) + 1; // 当前所取的p值！         LL t1 = ask(1, p, k, co);         if (t1 == -1){             LL t2 = ask(1, 1, p-1, co);             if (t2 != -1){                 cnt[t2] ++;                 res = max(res, cnt[t2]);                 change(1, t2, co + t);             }         }         else{             cnt[t1] ++;             res = max(res, cnt[t1]);             change(1, t1, co + t);         }     }     bool flag = false;     for (int i = 1; i <= k; i ++){         if (!flag && cnt[i] == res) {             printf("%lld", i-1);             flag = true;         }         else if (cnt[i] == res) printf(" %lld", i-1);     }     return 0; }

实习编辑：王晓姣

稿件来源：深度学习与文旅应用实验室（DLETA）