线性神经网络及其应用神经网络三
Posted 张叔zhangshu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性神经网络及其应用神经网络三相关的知识,希望对你有一定的参考价值。
线性神经网络典型案例分析
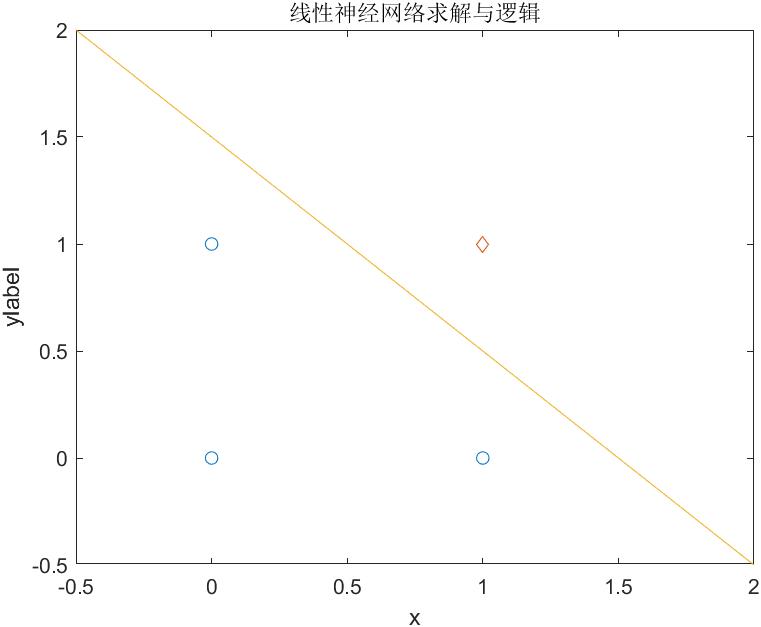
【例4-1】逻辑与有2个输入、1个输出,因此对应的线性网络有2个输入节点和1个输出节点,如图4-1所示。
由于方程的个数超过了自变量的个数,因此方程没有精确解,只有近似解,用伪逆法可以求得权值向量的值。
clear all;
%% 定义变量
P=[0,0,1,1;0,1,0,1] %输入向量
d=[0,0,0,1] %期望输出向量
lr=maxlinlr(P,'bias') %根据输入矩阵求解最大学习率
%% 线性网络实现
net1=linearlayer(0,lr); %创建线性网络
net1=train(net1,P,d); %线性网络训练
%% 显示
disp('线性网络输出') %命令行输出
Y1=sim(net1,P)
disp('线性网络二值输出');
YY1=Y1>=0.5
disp('线性网络最终权值:')
w1=[net1.iw{1,1}, net1.b{1,1}]
plot([0,0,1],[0,1,0],'o'); %图形窗口输出
hold on;
plot(1,1,'d');
x=-2:.2:2;
y1=1/2/w1(2)-w1(1)/w1(2)*x-w1(3)/w1(2); %1/2是区分0和1的阈值
plot(x,y1,'-');
axis([-0.5,2,-0.5,2])
xlabel('x');ylabel('ylabel');
title('线性神经网络求解与逻辑')
线性神经网络概述
线性神经元的结构

初始化线性神经网络
与感知器神经网络相同,线性神经网络的初始化也采用init函数实现。init函数的调用格式如下:
net=init(net);
使用上述语句,网络的权值和阈值被设置为0。MATLAB神经网络工具箱中的newlin函数和newlind函数均可以产生一个单层线性网络,在这两个函数中使用init函数,因此得到的线性网络已经是初始化的。
【例4-2】用newlin函数设计双输入单输出的线性神经网络,要求显示其权值和阈值。
程序实现代码如下:
>> clear all;
net=newlin([-1,1;-1,1],1);
>> net.iw{1}
ans =
0 0
>> net.b{1}
网络的学习规则

学习率的选择


网络的训练
【例4-3】设计一个双输入线性神经网络,输入范围为[-2,2;-2,2],学习率为1。
程序实现代码如下:
>> clear all;
P = [2 1 -2 -1;2 -2 2 1];
t = [0 1 0 1];
pr=[-2 2; -2 2];
net = newlin(pr,1);
net.trainParam.goal= 0.1;
[net, tr] = train(net,P,t);
disp('经过训练后的权值:')
w= net.iw{1,1}
disp('经过训练后的阈值:')
b=net.b{1}
disp('仿真验证:')
y=net(P)
disp('显示计算误差:')
err=t-y
线性神经网络工具箱函数
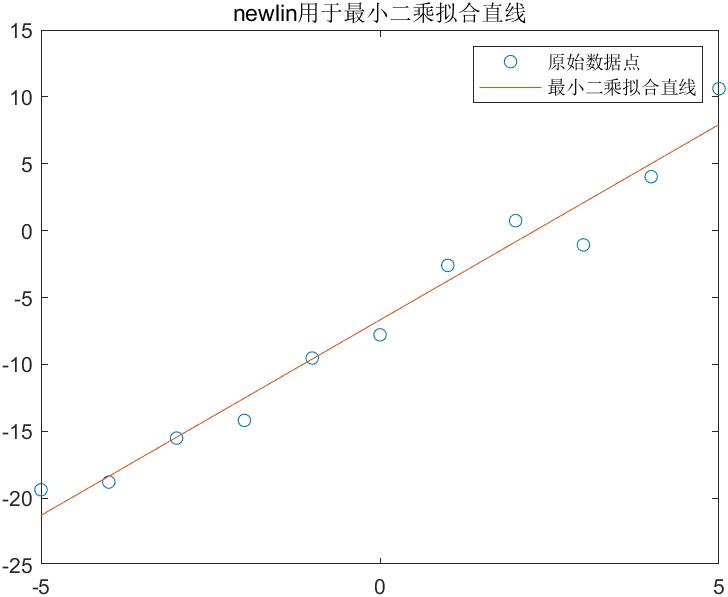
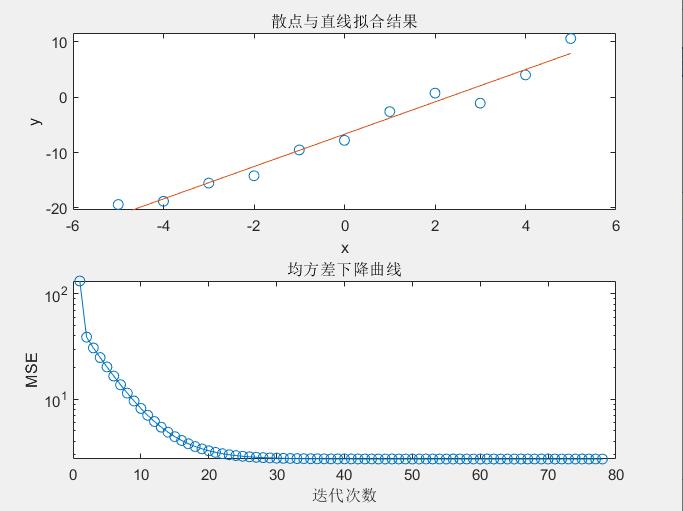
【例4-4】用newlin函数创建一个线性神经网络,并进行直线拟合。
程序实现代码如下:
>> clear all;
x=-5:5;
y=3*x-7; %直线方程
randn('state',2); %设置种子,便于重复执行
y=y+randn(1,length(y))*1.5; %加入噪声的直线
plot(x,y,'o');
P=x;T=y;
net=newlin(minmax(P),1,[0],maxlinlr(P)); %用newlin函数创建线性网络
%训练。与newlind函数不同,newlin函数创建的网络需要调用训练函数
tic;net=train(net,P,T);toc
new_x=-5:.2:5;
new_y=sim(net,new_x); %仿真
hold on;plot(new_x,new_y);
legend('原始数据点','最小二乘拟合直线');
title('newlin用于最小二乘拟合直线');
disp('权值为:')
net.iw
disp('偏置为:')
net.b
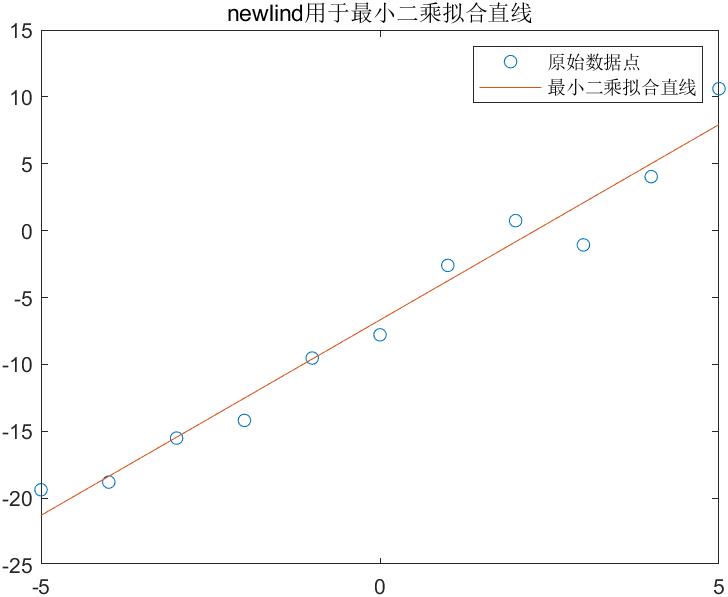
【例4-5】利用newlind函数对【例4-4】的数据进行拟合。
程序实现代码如下:
>> clear all;
x=-5:5;
y=3*x-7; %直线方程
randn('state',2); %设置种子,便于重复执行
y=y+randn(1,length(y))*1.5; %加入噪声的直线
plot(x,y,'o');
P=x;T=y;
net=newlind(P,T); %用newlind函数建立线性层
new_x=-5:.2:5; %新的输入样本
new_y=sim(net,new_x); %仿真
hold on;plot(new_x,new_y);
legend('原始数据点','最小二乘拟合直线');
disp('权值为:')
net.iw
disp('偏置为:')
net.b
title('newlind用于最小二乘拟合直线');
linearlayer函数是MATLAB R2020的神经网络工具箱中增加的,该函数用来替代newlin函数,用于设计静态或动态的线性系统,函数的调用格式如下:
linearlayer(inputDelays,widrowHoffLR)
其中,参数inputDelays为输入延迟的行向量,默认值为1:2;widrowHoffLR为学习率,默认值为0.01。
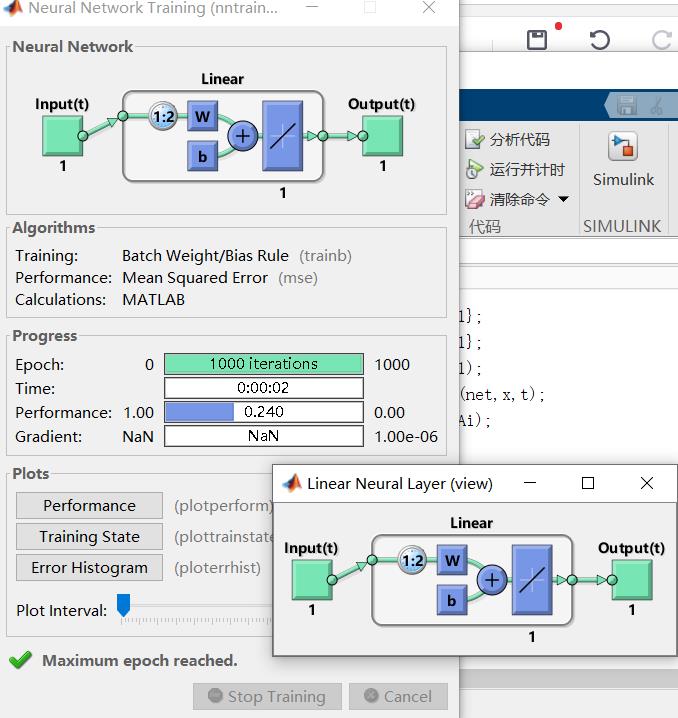
【例4-6】利用linearlayer函数创建一个线性神经网络。
程序实现代码如下:
>> clear all;
x = {0 -1 1 1 0 -1 1 0 0 1};
t = {0 -1 0 2 1 -1 0 1 0 1};
net = linearlayer(1:2,0.01);
[Xs,Xi,Ai,Ts] = preparets(net,x,t);
net = train(net,Xs,Ts,Xi,Ai);
view(net)
Y = net(Xs,Xi);
perf = perform(net,Ts,Y)
学习函数
【例4-7】利用learnwh函数对散点及带噪声的线性函数进行学习,并对散点与函数进行拟合。
程序实现代码如下:
>> clear all;
%%定义数据
P=-5:5; %输入:11个标量
d=3*P-7;
randn('state',2);
d=d+randn(1,length(d))*1.5 %期望输出:加了噪声的线性函数
P=[ones(1,length(P));P] %P加上偏置
lp.lr = 0.01; %学习率
MAX = 150; %最大迭代次数
ep1 = 0.1; %均方差终止阈值
ep2 = 0.0001; %权值变化终止阈值
%%初始化
w=[0,0];
%%循环更新
for i=1:MAX
fprintf('第%d次迭代:\\n', i)
e=d-purelin(w*P); %求得误差向量
ms(i)=mse(e); %均方差
2)maxlinlr函数
maxlinlr为分析函数,用于计算线性层的最大学习率,函数的调用格式如下:
lr = maxlinlr§
其中,输入参数P为R×Q维矩阵,对不带阈值的线性层得到一个所需要的最大学习率lr。
lr=maxlinlr(P, ‘bias’)
其中,针对带有阈值的线性层得到一个所需要的最大学习率。
【例4-8】计算输入矩阵的最大学习率。
程序实现代码如下:
>> clear all;
>> P = [1 2 -4 7; 0.1 3 10 6];
>> lr=maxlinlr(P,'bias') %带偏置时的最大学习率
lr =
0.0067
>> lr=maxlinlr(P) %不带偏置时的最大学习率
lr =
0.0069
>> lr=0.9999/max(eig(P*P')) %检验最大学习率
lr =
0.0069
传递函数
info = purelin(‘code’)
依据code值的不同,返回不同的信息。当code=name时,返回传递函数的全称;当code=active时,返回有传递函数最小值、最大值的有效输入范围;当code=output时,返回有传递函数最小值、最大值的二元矢量;当code=fullderiv时,根据dA_dN是S×S×Q还是S×Q来确定返回1还是0;当code=fpnames时,返回函数参数的名称;当code=fpdefaults时,返回默认的函数参数。
【例4-9】利用purelin函数产生一个线性传递函数。
程序实现代码如下:
>> clear all;
n = -5:0.1:5;
a = purelin(n);
plot(n,a)
网络的局限性
相关向量
【例4-11】给定输入向量P和期望输出向量T进行训练。
程序实现代码如下:
>> clear all;
P=[1.0 2.0 3.0;4.0 5.0 6.0];
T=[0.5 1.0 -1.0];
lr=maxlinlr(P,'bias');
net = newlin([0 10;0 10],1,[0],lr);
net.trainParam.show=50;
net.trainParam.epochs=500;
net.trainParam.goal=0.001;
[net,tr]=train(net,P,T);
学习率过大
在网络设计中,学习率的选取是影响收敛速度及训练结果的重要因素。当学习率过小时,依据W-H学习规则总能够训练网络满足精度要求;但是,当学习率过大时,则可能导致训练过程的不稳定。MATLAB神经网络工具箱函数给出了一个正确求解学习率的maxlinlr函数。
【例4-12】选择两个一维输入向量及相应的期望输出向量。
程序实现代码如下:
>> clear all;
P=[+1.0 -1.2];
T=[+0.5 +1.0];
%给出权值和阈值范围并绘制误差曲面及等高线,如图4-15所示
w_range=-2:0.4:2;
b_range=-2:0.4:2;
ES=errsurf(P,T,w_range,b_range,'purelin');
plotes(w_range,b_range,ES);
lr=maxlinlr(P,'bias');
net=newlin([-2 2],1,[0],lr*2.25);
net.trainparam.epochs=20;
线性神经网络的应用
1.逻辑异或
1)二值逻辑与
4.1节已经通过MATLAB程序手算实现了二值逻辑与问题,下面直接通过工具箱函数实现。
【例4-13】利用工具箱函数实现【例4-1】的二值逻辑与问题的求解。
>> clear all;
%%定义变量
P=[0,0,1,1;0,1,0,1] %输入向量
d=[0,0,0,1] %期望输出向量
lr=maxlinlr(P,'bias') %根据输入矩阵求解最大学习率
%%线性网络的实现
net1=linearlayer(0,lr); %创建线性网络
net1=train(net1,P,d); %训练线性网络
%%感知器的实现
net2=newp([-1,1;-1,1],1,'hardlim'); %创建感知器
net2=train(net2,P,d);
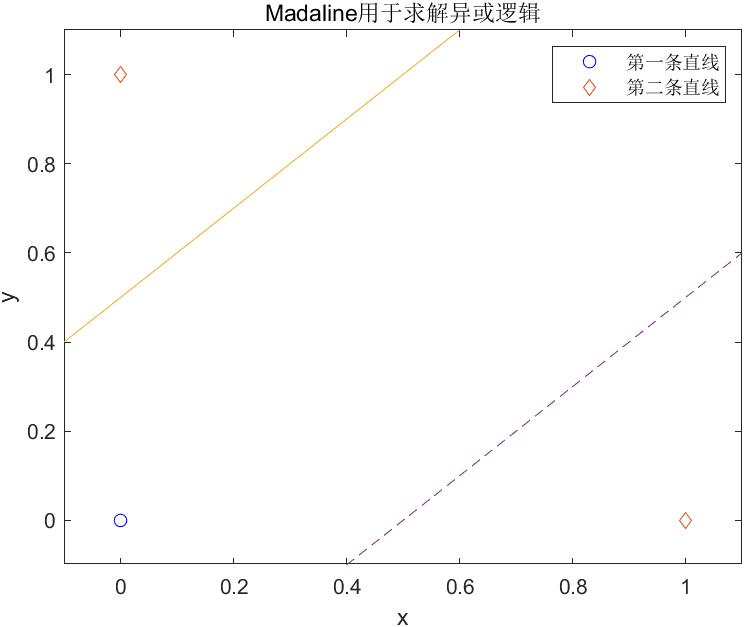
2)二值逻辑异或
【例4-14】为线性网络添加如图4-6所示的非线性输入,其使用两个神经元的Madaline神经网络,结构如图4-4所示。
解析:两个神经元的输出必须取一次与非,最后得到的结果才符合异或运算的定义。实现的MATLAB代码如下:
>> clear all;
%%第一个神经元
P1=[0,0,1,1;0,1,0,1]; %输入向量
d1=[1,0,1,1]; %期望输出向量
lr=maxlinlr(P1,'bias'); %根据输入矩阵求解最大学习率
net1=linearlayer(0,lr); %创建线性网络
net1=train(net1,P1,d1); %训练线性网络
%%第二个神经元
P2=[0,0,1,1;0,1,0,1]; %输入向量
d2=[1,1,0,1]; %期望输出向量
lr=maxlinlr(P2,'bias'); %根据输入矩阵求解最大学习率
net2=linearlayer(0,lr); %创建线性网络
net2=train(net2,P2,d2); %训练线性网络
Y1=sim(net1,P1);Y1=Y1>=0.5;
Y2=sim(net2,P2);Y2=Y2>=0.5;
以自适应线性网络实现噪声降噪处理。
解析:假设传输信号为余弦波信号,噪声为随机噪声,进行自适应神经网络设计。
根据以上分析,自适应线性神经元的输入向量为随机噪声;余弦波信号与随机噪声之和为神经元的目标向量;输出信号为网络调整过程中的误差信号。实现噪声降噪的MATLAB代码如下:
>> clear all;
%%定义输入向量和目标向量
t=0.01:0.02:20; %时间变量
zs=(rand(1,1000)-0.5)*10; %随机噪声
input=cos(t);
P=zs;
T=input+zs; %目标向量
%%创建线性神经网络
net=newlin([-1 1],1,0,0.0005);
%%神经网络自适应训练
net.adaptParam.passes=70;
[net,y,output]=adapt(net,P,T); %输出信号output为网络调整过程中的误差
%%绘制信号波形
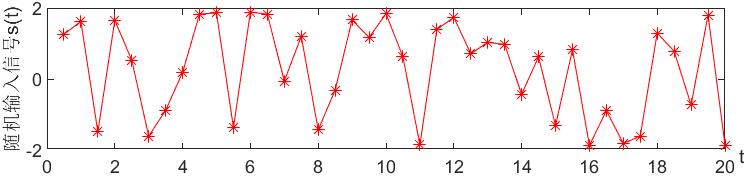
【例4-16】实现自适应预测的线性网络。假设自适应滤波器如图4-24所示,该滤波器的目的是根据输入信号的前两个时刻的值预测当前时刻的值。
假设输入信号为随机序列,请尝试编写MATLAB程序,并画出上述自适应滤波器的输入/输出波形。
其实现的MATLAB程序代码如下:
>> clear all;
%定义输入向量和目标向量
time=0.5:0.5:20; %时间变量
y=(rand(1,40)-0.5)*4; %定义随机输入信号
p=con2seq(y); %将随机输入向量转换为串行向量
delays=[1 2]; %定义自适应线性神经元输入延迟量
t=p; %定义自适应线性神经元的数目向量
%创建线性神经网络
net=newlin(minmax(y),1,delays,0.0005);
%线性神经网络的自适应调整(训练)
net.adaptParam.passes=70;
[net,a,output]=adapt(net,p,t); %输出信号output为网络调整过程中的误差
%绘制随机输入信号/输出信号的波形
hold on;
subplot(3,1,1);plot(time,y,'r*-');
xlabel('t','position',[20.5,-1.8]);ylabel('随机输入信号s(t)');
以上是关于线性神经网络及其应用神经网络三的主要内容,如果未能解决你的问题,请参考以下文章