数据结构与算法笔记（十五）—— 散列(哈希表)

Posted 2021-10-12 别呀

一、前沿

1.1、直接寻址表

当关键字的全域U比较小时，直接寻址是一种简单而有效的技术。假设某应用要用到一个动态集合，其中每个元素都有一个取自全域U={0，1，…，m-1)的关键字，此处m是一个不很大的数。另假设没有两个元素具有相同的关键字。

为表示动态集合，我们用一个数组(或称直接寻址表)T[0…m一1]，其中每个位置（或称槽）应全域U中的一个关键字。下图说明这个方法；槽 k 指向集合中一个关键字为 k 的元素。如果该集合中没有关键字为 k 的元素，则T[k]=NIL。

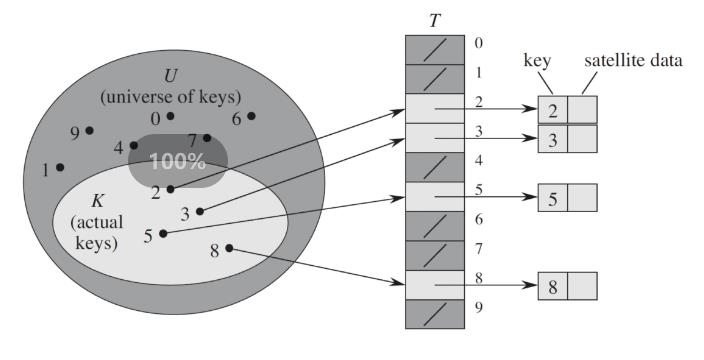
用一个直接寻址表T实现动态集合。全域U={0，1，…，9}中的每个关键字都对应于表中的一个下标值。由实际关键字构成的集合K={2，3，5，8}决定表中哪些槽包含指向元素的指针。其他带深阴影的槽包含NIL

直接寻址技术缺点:

• 当域U很大时，需要消耗大量内存，很不实际
• 如果域U很大而实际出现的key很少，则大量空间被浪费
• 无法处理关键字不是数字的情况

---

1.2、哈希

直接寻址表：key为k的元素放到k位置上

改进直接寻址表：哈希(Hashing)

• 构建大小为m的寻址表T
• key为k的元素放到h(k)位置上
• h(k)是一个函数，其将域U映射到表T[0,1,…,m-1]

---

二、哈希表

2.1、概念

哈希表（Hash Table，又称为散列表），是—种线性表的存储结构。哈希表由一个直接寻址表和一个哈希函数组成。哈希函数h(k)将元素关键字k作为自变量，返回元素的存储下标。

哈希表一个通过哈希函数来计算数据存储位置的数据结构，通常支持如下操作:

• insert(key,value)：插入键值对(key,value)
• get(key)：如果存在键为key的键值对则返回其value，否则返回空值
• delete(key)：删除键为key的键值对

例：假设有一个长度为7的哈希表，哈希函数h(k)=k%7。元素集合{14,22,3,5}的存储方式如下图：

---

2.2、哈希冲突

由于哈希表的大小是有限的，而要存储的值的总数量是无限的，因此对于任何哈希函数，都会出现两个不同元素映射到同一个位置上的情况，这种情况叫做哈希冲突。

2.2.1、解决哈希冲突——开放寻址法

开放寻址法：如果哈希函数返回的位置已经有值，则可以向后探查新的位置来存储这个值

• 线性探查：如果位置i被占用，则探查i+1, i+2,…
• 二次探查：如果位置i被占用，则探查i+1^2, i-1^2, i+2^2, i-2^2,…
• 二度哈希：有n个哈希函数，当使用第1个哈希函数h1发生冲突时，则尝试使用h2,h3,…

---

2.2.2、解决哈希冲实——拉链法

拉链法:哈希表每个位置都连接—个链表，当冲突发生时，冲突的元素将被加到该位置链表的最后。

---

2.3、常见哈希函数

除法哈希法

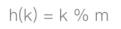
乘法哈希法

全域哈希法

---

三、哈希表实现(拉链法)

链表代码（单链表）：数据结构与算法笔记（三）—— 链表(单链表、循环链表、双向链表)

class HashTable:
    def __init__(self,size = 20):
        self.size = size
        self.T = [SingleLinkList() for i in range(self.size)]

    def h(self,k):
        '''哈希函数: 计算数据存储位置'''
        return k % self.size

    def insert(self,k):
        '''插入元素'''
        i = self.h(k)
        if self.find(k):
            print('重复插入!!!')
        else:
            self.T[i].append(k)

    def find(self,k):
        '''查找元素'''
        i = self.h(k)
        return self.T[i].search(k)

    def travel(self):
        '''遍历打印'''
        for i in range(self.size):
            print(self.T[i].travel())

    def remove(self,k):
        '''删除元素'''
        if self.find(k):
            i = self.h(k)
            self.T[i].remove(k)
            
if __name__ == '__main__':
	ht = HashTable()
	ht.insert(0)
	ht.insert(1)
	ht.insert(2)
	ht.insert(21)
	ht.travel()
	ht.remove(2)
	ht.travel()
	print(ht.find(2))

---

四、哈希表的应用

4.1、集合与字典

字典与集合都是通过哈希表来实现的。

例如：

a = {'name': 'Alex', 'age': 18, 'gender': 'Man'}

使用哈希表存储字典，通过哈希函数将字典的键映射为下标。
假设：

h('name')=3, h('age')=1, h('gender')=4

则哈希表存储为

[None,18,None,'Alex','Man']

如果发生哈希冲突，则通过拉链法或开发寻址法解决

---

4.2、md5算法

MD5(Message-Digest Algorithm 5)曾经是密码学中常用的哈希函数，可以把任意长度的数据映射为128位的哈希值，其曾经包含如下特征:

1. 同样的消息，其MD5值必定相同;
2. 可以快速计算出任意给定消息的MD5值;
3. 除非暴力的枚举所有可能的消息，否则不可能从哈希值反推出消息本身;
4. 两条消息之间即使只有微小的差别，其对应的MD5值也应该是完全不同、完全不相关的;
5. 不能在有意义的时间内人工的构造两个不同的消息使其具有相同的MD5值。

应用举例： 文件的哈希值

算出文件的哈希值，若两个文件的哈希值相同，则可认为这两个文件是相同的，因此：

1. 用户可以利用它来验证下载的文件是否完整。
2. 云存储服务商可以利用它来判断用户要上传的文件是否已经存在于服务器上，从而实现秒传的功能，同时避免存储过多相同的文件副本。

---

4.3、SHA2算法

历史上MD5和SHA-1曾经是使用最为广泛的 cryptographic hash function，但是随着密码学的发展,这两个哈希函数的安全性相继受到了各种挑战。

因此现在安全性较重要的场合推荐使用SHA-2等新的更安全的哈希函数。

SHA-2包含了一系列的哈希函数: SHA-224，SHA- 256，SHA-384，SHA-512，SHA-512/224，SHA- 512/256，其对应的哈希值长度分别为224，256，384 or 512位。

SHA-2具有和MD5类似的性质(参见MD5算法的特征)。

应用举例：
例如，在比特币系统中，所有参与者需要共同解决如下问题：对于一个给定的字符串U，给定的国标哈希值H，需要计算出一个字符串V，使得U+V的哈希值与H的差小于一个给定值D。此时，只能通过暴力枚举V来进行猜测。首先计算出结果的人可获得一定奖金。而某人首先计算成功的概率与其拥有的计算量成正比，所以其获得的奖金的期望值与其拥有的计算量成正比。