线段树-维护区间最小值和区间和2021 ICPC网络赛第一场 D: Edge of Taixuan

Posted 2021-10-12 biu~跃哥冲冲冲

Problem D: Edge of Taixuan

评测传送门
(ps: 评测时需要先花费一个币买下题目集后方可进行提交并评测。)



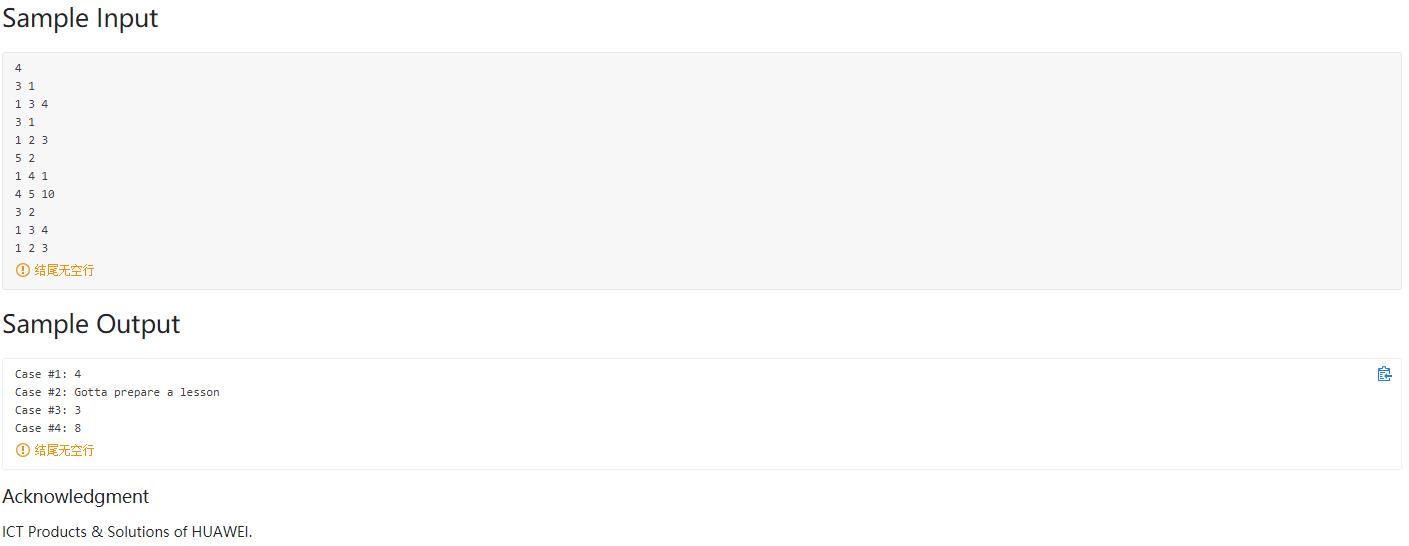
题目大意：
给出 $n$个结点，$m$次操作,每次操作给出一个区间 $[l,r]$,和一个权值$w$，建立 $l$ 到 $r$ 的完全图，边权均是 $w$。 计算出 “所有边的权值之和” 减去 “包含 $n$ 个结点的最小生成树的权值”为最终所求答案，若无法构成最小生成树，输出指定字符串即可。

解题思路：
对于“所有边的权值之和”很容易就能求出来，简单画个图就很清楚的可以看出来，不再多余赘述。
重头戏是如何去求 “包含 $n$ 个结点的最小生成树的权值”。
直接用最小生成树算法是可以求出来，但是奈何边的数量太多了，在这个题上并不实用。
由于每一部分都是完全图，完全图内部怎样相连都是可以的，不妨就认为它的连接方式是: “1-2-3…”。用线段树维护 $n-1个点$，对于当前第 $i$ 个点，它的值指的是将 $i$ 和 $i+1$连起来的最小权值。
求出所有 $n-1$ 个点的权值之和即为最小生成树的权值。

线段树中维护一个区间最小值、区间和，懒惰标记来实现更新与求所有点的权值之和的操作。

将所有操作按照权值从大到小排序，依次更新区间最小值和区间和。由于是从大到小排序，因此每个点维护的信息，都会被更新到最优。

AcCoding:

#pragma G++ optimize(2)
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100010;
struct Tree {
	int l, r;
	ll sum;
	int min1, lazy;
}tree[4 * N];
struct Edge {
	int l, r, w;
	bool operator<(const Edge x)const {
		return w > x.w;
	}
}e[N];
void pushup(int u)
{
	tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum;
	tree[u].min1 = min(tree[u << 1].min1, tree[u << 1 | 1].min1);
}
void pushdown(int u)
{
	if (tree[u].lazy != 0)
	{
		tree[u << 1].lazy = tree[u].lazy;
		tree[u << 1 | 1].lazy = tree[u].lazy;
		tree[u << 1].sum = 1ll * tree[u].lazy * (tree[u << 1].r - tree[u << 1].l + 1);
		tree[u << 1 | 1].sum = 1ll * tree[u].lazy * (tree[u << 1 | 1].r - tree[u << 1 | 1].l + 1);
		tree[u << 1].min1 = tree[u].lazy;
		tree[u << 1 | 1].min1 = tree[u].lazy;
		tree[u].lazy = 0;
	}
}
void build(int u, int l, int r)
{
	tree[u] = { l,r,0,0,0 };
	if (l == r) return;
	int mid = l + r >> 1;
	build(u << 1, l, mid);
	build(u << 1 | 1, mid + 1, r);
	pushup(u);
}
void update(int u, int l, int r,int w)
{
	if (l <= tree[u].l && tree[u].r <= r)
	{
		tree[u].sum = 1ll * (tree[u].r - tree[u].l + 1) * w;
		tree[u].lazy = tree[u].min1 = w;
		return;
	}
	pushdown(u);
	int mid = tree[u].l + tree[u].r >> 1;
	if (l <= mid) update(u << 1, l, r, w);
	if (r > mid) update(u << 1 | 1, l, r, w);
	pushup(u);
}
ll query(int u, int l, int r)
{
	if (l <= tree[u].l && tree[u].r <= r)
	{
		return tree[u].sum;
	}
	pushdown(u);
	int mid = tree[u].l + tree[u].r >> 1;
	ll res = 0;
	if (l <= mid) res += query(u << 1, l, r);
	if (r > mid) res += query(u << 1 | 1, l, r);
	return res;
}
inline int read()
{
	int x = 0, f = 1;char ch = getchar();
	while (ch < '0' || ch>'9') { if (ch == '-')f = -1;ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0';ch = getchar(); }
	return x * f;
}
int main() {
	int t; t = read();
	int k = 0;
	while (t--) {
		int n, m; n = read(), m = read();
		build(1, 1, n - 1);
		ll res = 0;
		for (int i = 0;i < m;i++) {
			e[i].l = read(), e[i].r = read(), e[i].w = read();
			int cnt = e[i].r - e[i].l + 1;
			res += (ll)e[i].w * cnt * (cnt - 1) / 2;
		}
		sort(e, e + m);
		for (int i = 0;i < m;i++) update(1, e[i].l, e[i].r - 1, e[i].w);
		printf("Case #%d: ", ++k);
		ll sum = query(1, 1, n - 1);
		if (tree[1].min1) printf("%lld", res - sum);
		else printf("Gotta prepare a lesson");
		if (t >= 1) printf("\\n");
	}
	return 0;
}

参考博客
注意：这道题可能卡的比较严，一开始我按照从小到大排序，每次计算出未被更新到的点个数乘以当前变权值，来依次求最小生成树，最终答案无疑也是正确的，但就是会被卡得死死的。 无奈╮(╯▽╰)╭

收获：如何区间更新为同一个数？
方式1：区间乘0，再区间加。（常数偏大）
方式2：用区间加的方式，将更新过程中的 “+=” ,直接改为 “=” 即可。（常数更小）