3D数学基础：图形与游戏开发 第二章 笛卡尔坐标系统

Posted 2021-10-11 思航

目录

• 一、前言
• 二、1D数学
• 三、2D 笛卡尔数学
• 四、从2D到3D
• 五、思考题
• 六、总结

一、前言

大家好，我是思航。今天我们来学习本书的第二章。
计算机图形学第一准则：近似原则如果它看上去是对的它就是对的。

二、1D数学

计数（两千多年前的数羊）和度量的数学。
基本概念:

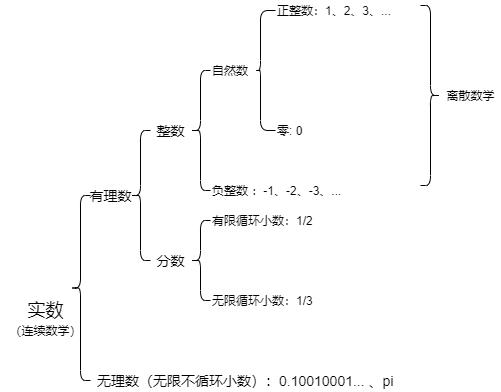
三、2D 笛卡尔数学

原点+两条轴（两条过原点且互相垂直的直线）
x轴、y轴
定位一个点，需要两个数 x和y。x表示该点到y轴的有符号距离
y表示该点到x轴的有符号距离

四、从2D到3D

相比2D，增加了第三个轴，z轴。
定位一个点，需要3个数：x,y和z。分别表示该点到yz，xz，和x平面的有符号距离

左手坐标系： 大拇指向右，食指向上，中指向前（后面补图）
右手坐标系：大拇指向左，食指向上，中指向前（后面补图）

拇指、食指和中指 分别代表 x、y、z的正方向

五、思考题

3D 笛卡尔坐标系一共有多少种不同的组合？

答案是48种。为什么呢？
根据定义，每个轴要互相垂直。首先我们x轴一共有6种选择，而那这样
y轴有4种选择。x和y轴确认后，z轴只有两种选择。
所以一共有 6 * 4 * 2=48种组合

六、总结

通过这章的学习，我们初步了解了3D坐标系的概念，在接下来的章节我们再深入学习一下。