2022计算机考研408—数据结构—排序
Posted 发呆哥o_o ....
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022计算机考研408—数据结构—排序相关的知识,希望对你有一定的参考价值。
手把手教学考研大纲范围内的排序
22考研大纲数据结构要求的是C/C++,笔者以前使用的都是Java,对于C++还很欠缺,
如有什么建议或者不足欢迎大佬评论区或者私信指出
排序定义
冒泡排序
直接插入排序
二分插入排序
希尔排序⭐
快速排序
二路归并排序⭐
基数排序(附加计数排序)⭐
简单选择排序
堆排序⭐⭐
排序
排序的基本概念
顾名思义,给一个无序数组的值进行顺序存储
原数组:2 3 1 5 6 4 8 9 7
排序后:1 2 3 4 5 6 7 8 9
冒泡排序
思路:
从头到尾每两个相邻的元素,进行比较,前面的比后面的大就进行交换
循环一遍后,数组元素最大的就到了最后面,
第二次循环的时候,就可以不循环到最后一个了,最后一个上次循环已经是整个数组最大的值了
然后把这次最大的放到倒数第二个元素,
第三次循环的就可以忽略最后两个元素
以此类推,全部循环后,即可完成排序
#include <iostream>
#include <vector>
using namespace std;
void bubbleSort(vector<int> &num);
int main() {
int n; //n为将要输入的数组长度
cin >> n; //输入n cin方法需要上面使用std
vector<int> num; //定义vector 记得上面导入vector
int temp; //temp为输入vector时的中间变量
for (int i = 0; i < n; i++) {
cin >> temp; //输入
num.push_back(temp);
}
bubbleSort(num); //调用自定义的排序方法
cout << "排序后" << "\\n";
for (int i = 0; i < num.size(); i++) {
cout << num[i] << " "; //输出
}
return 0;
}
void bubbleSort(vector<int> &num) {
for (int i = 0; i < num.size(); i++) {
for (int j = 0; j < num.size() - i; j++) {
if (num[j] > num[j + 1]) {
// int temp = num[j];
// num[j] = num[j + 1];
// num[j + 1] = temp;
num[j] ^= num[j + 1]; //两两相邻交换 上面注释代码的功能与此功能相等
num[j + 1] ^= num[j];
num[j] ^= num[j + 1];
}
}
//每次循环都把数组的变动输出出来
for (int j = 0; j < num.size(); j++) {
cout << num[j] << " ";
}
cout << "\\n";
}
}

直接插入排序
思路:
插入 == 把数插进去
也是两层循环
数组num
第一层循环从下标为1的值开始,循环变量为i
第二层循环就是把第一层的值拿出来,然后从第i-1个向前循环,找到第一个小于 num[i] 的值,
这个值的下标如果是j-1的话,那么 num[j] 就是第一个大于 num[i] 的值
把 num[i] 用一个变量 temp 保存一下
把下标为j到i-1的值依次向后移动一位,也就是说下标j到i-1的值移动到j+1到i,
然后把 temp(原num[i])放到下标为j的地方(之前的num[j]已经移动到num[j+1]了),
按照这种排序,每次循环的都是i之前的,i之前的元素都是顺序存储的,
文字表述的不清楚的可以看每次循环i更改后数组的元素情况
#include <iostream>
#include <vector>
using namespace std;
void insertSort(vector<int> &num);
int main() {
int n; //n为将要输入的数组长度
cin >> n; //输入n cin方法需要上面使用std
vector<int> num; //定义vector 记得上面导入vector
int temp; //temp为输入vector时的中间变量
for (int i = 0; i < n; i++) {
cin >> temp; //输入
num.push_back(temp);
}
insertSort(num); //调用自定义的排序方法
cout << "排序后" << "\\n";
for (int i = 0; i < num.size(); i++) {
cout << num[i] << " "; //输出
}
return 0;
}
void insertSort(vector<int> &num) {
for (int i = 1; i < num.size(); i++) {
int temp = num[i]; //保存一下num[i]
int j;
//从num[j]向前开始找,一直找到比temp(原num[i])小的数就结束
//在循环过程中的数都比temp大的,不断地把temp大的数往后移动一位
//由此可得,等找到num[j]<=temp的时候,循环已经结束了
// 但是他的上一个,也就是num[j+1]的值已经移动到num[j+2]了
for (j = i - 1; j >= 0 && num[j] > temp; j--) {
num[j + 1] = num[j];
}
//可以直接把temp放到num[j+1],
num[j + 1] = temp;
//每次循环都可以把num[i]以及之前的数值排序好
//每次循环都把数组的变动输出出来
for(j = 0; j < num.size(); j++) {
cout << num[j] << " ";
}
cout <<"\\n";
}
}
运行截图:

二分插入排序
思路:
二分插入和简单插入基本类似
不过是在寻找插入位置的时候不在采用简单插入的循环查找,而是使用二分查找
减少比较的次数,提升效率
#include <iostream>
#include <vector>
using namespace std;
void binInsertSort(vector<int> &num);
int main() {
int n; //n为将要输入的数组长度
cin >> n; //输入n cin方法需要上面使用std
vector<int> num; //定义vector 记得上面导入vector
int temp; //temp为输入vector时的中间变量
for (int i = 0; i < n; i++) {
cin >> temp; //输入
num.push_back(temp);
}
binInsertSort(num); //调用自定义的排序方法
cout << "排序后" << "\\n";
for (int i = 0; i < num.size(); i++) {
cout << num[i] << " "; //输出
}
return 0;
}
void binInsertSort(vector<int> &num) {
for (int i = 1; i < num.size(); i++) {
int temp = num[i]; //保存临时变量
int left = 0; //使用二分法找到插入的位置left 使得num[left]<temp<num[left+1]
int right = i - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (num[mid] > temp) {
right = mid - 1;
} else {
left = mid + 1;
}
}
for (int j = i - 1; j >= left; j--) {
num[j + 1] = num[j]; //把left右面的值全部右移一位,
}
num[left] = temp; //把temp放到num[left]的位置
//每次循环都把数组的变动输出出来
for (int j = 0; j < num.size(); j++) {
cout << num[j] << " ";
}
cout << "\\n";
}
}

希尔排序
思路:
希尔排序其实可以看做是插入排序的变种
插入排序是循环到某个元素就像前找合适的位置,把当前元素到合适位置的值都要向后移动一遍
插入排序对于有序的数组,比较和移动的次数都比较少
希尔排序就是把插入排序进行分组化
分组是按照长度每次除2分的,这样最后一次肯定是一个组一个元素,就相当于最原始的插入排序了
而他前面做的按组排序就是为了让这个数组变成一个有大概顺序的数组,使后面的插入排序能减少比较和移动的次数
按下图为例子,数组长度15 第一次按照7个增量分组,第二次按照3个增量,第三次按照1个增量分组
第一次循环的增量为7
第一次是下标 0 与 0+7比较 1与1+7比较 …… 7 与 7+7比较
第一次循环完,这些位置上有了个大概的顺序
第二次循环的增量为3
第二次是下标 0与3与6与9与12比较 1与4与7与10与13 2与5与8与11与14
第二次循环完,这些位置上有了大概的顺序
第三次循环的增量为1
就相当于简单的插入排序
希尔排序的精髓就在于,对于一个大概有序的数组,插入排序的比较和移动次数都比较少
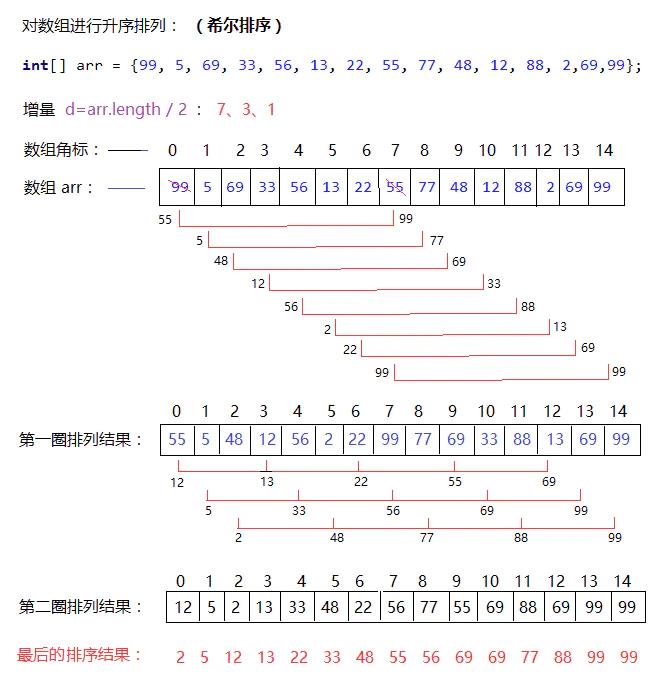
PS:小编作图能力有限,上图是当来的
//除main方法外的其他cout输出都是为了让读者更清楚的了解每次循环后进行排序的下标
#include <iostream>
#include <vector>
using namespace std;
void shellSort(vector<int> &num);
int main() {
int n; //n为将要输入的数组长度
cin >> n; //输入n cin方法需要上面使用std
vector<int> num; //定义vector 记得上面导入vector
int temp; //temp为输入vector时的中间变量
for (int i = 0; i < n; i++) {
cin >> temp; //输入
num.push_back(temp);
}
shellSort(num); //调用自定义的排序方法
cout << "\\n\\n排序后" << "\\n";
for (int i = 0; i < num.size(); i++) {
cout << num[i] << " "; //输出
}
return 0;
}
void shellSort(vector<int> &num) {
int len = num.size();
for (int d = len / 2; d > 0; d/=2) { //按照增量分组,增量每次/2
cout << "\\n\\n增量为" << d;
for (int i = d; i < len; i++) { //类似插入排序,每次都比较i之前的,
cout << "\\n此次排序的下标为:" << i;
for (int j = i - d; j >=0; j-=d) {
cout << " " << j;
//这里i-d其实也就是从前面开始,
// j每次都是j-=d,因为我们是按照相同增量分为一组的
// 对比上图更容易理解
if (num[j] > num[j + d]) { //只要前面的比后面的大,就交换位置
int temp = num[j];
num[j] = num[j + d];
num[j + d] = temp;
}
}
//每次循环都把数组的变动输出出来
cout << "\\n";
for (int j = 0; j < num.size(); j++) {
cout << num[j] << " ";
}
}
}
}

快速排序
思路:
从未排序的数组中,一个一个的寻找,寻找当前值应该在排序后数组的位置,
以此类推,把每个值的位置都确定了以后,此数组就变成了排序后的数组
也是分段进行确定某个值最终排序后的下标
先选取第一个值,用一个临时变量保存这个值,然后双指针i表示这段范围的开头,j这段范围的结尾
j负责从后向前找小于临时变量的值,找到以后就把j的值放到i那,
此时j位置就空出来了,我们当作把临时变量的值放到j这里
i负责从前向后找大于临时变量的值,找到后就放到j那里,
此时i位置就空出来了,我们同样当作把临时变量的值放到i这里
不断循环这两步的操作,
i是从前向后,j是从后向前
循环结束的条件就是i==j 也就是临时变量排序后数组的位置,
按照这种排序方式,结束后,
比临时变量小的都在临时变量左边(左边不一定是排好序的),
比临时变量大的都在临时变量右边(右边不一定是排好序的),
当前临时变量的位置确定好以后,我们可以分为前半部分和后半部分继续这种操作
以此类推,当每个值最终排序后的位置都确定的时候,此数组为排序后的数组
下图为确定好一个值的最终位置的排序图
临时变量为50,左指针low,右指针high

右指针找到20比临时变量小,交换两个值
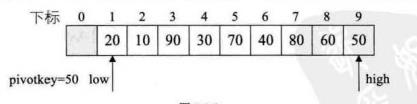
左指针找到90比临时变量大,交换两个值

右指针找到40比临时变量小,交换两个值位置
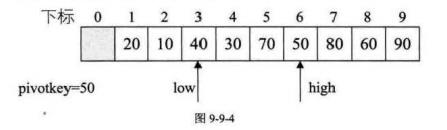
左指针找到70比临时变量小,交换两个值的位置

右指针左移与左指针重合,当前位置为50排序后的最终位置
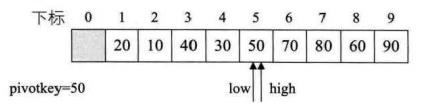
我们发现,左边的数都比50小,右边的数都比50大,
然后在把左边的数组按照这种方法,右边的数组按照这种方法
以此类推每个值的最终下标都确定下来了,数组为排序后的数组
PS:图仍然是某度当来的o( ̄▽ ̄)ブ
#include <iostream>
#include <vector>
using namespace std;
void quickSort(vector<int> &num, int left, int right);
int main() {
int n; //n为将要输入的数组长度
cin >> n; //输入n cin方法需要上面使用std
vector<int> num; //定义vector 记得上面导入vector
int temp; //temp为输入vector时的中间变量
for (int i = 0; i < n; i++) {
cin >> temp; //输入
num.push_back(temp);
}
quickSort(num, 0, num.size() - 1); //调用自定义的排序方法
cout << "\\n\\n排序后" << "\\n";
for (int i = 0; i < num.size(); i++) {
cout << num[i] << " "; //输出
}
return 0;
}
void quickSort(vector<int> &num, int left, int right) {
if (left >= right) return; //如果左节点>=右节点了,证明排序结束了,返回即可
int temp = num[left]; //保存一下当前左节点的值,此次排序就是确定当前左节点的值
int l = left; //保存一下原始的左右边界
int r = right;
while (left < right) { //循环的结束条件就是左指针 == 右指针,相等时就为temp排序后的最终位置
while (left < right && temp < num[right]) { //右指针找比temp小的值,如果没找到就一直找
right--;
}
if (left < right) { //上面循环结束了就证明找到了,如果left == right,那么最终位置就确定好了,
num[left] = num[right]; //然后把比temp小的放到左面left位置那里,然后left指向下一个值
left++; //可能这里有些疑问,上面描述的是交换,这里没有交换,实际上每次都交换,换来换去,每次都重复换temp这个数
} //不如直接赋值,然后把这个重复数直接放到最后确定的位置
while (left < right && num[left] < temp) { //这里是左指针找比temp大的数,找到就退出循环了,
left++;
}
if (left < right) { //与上面相反的道理,把比temp大的数放到right,right指针左移
num[right] = num[left];
right--;
}
}
num[left] = temp; //循环结束就是确定了temp最终的位置,左指针==右指针
//每次循环都把数组的变动输出出来
cout << "\\n左边界下标:" << l << " 右边界下标:" << r << " 当前循环确定的下标为:" << left << "\\n";
for (int j = 0; j < num.size(); j++) {
cout << num[j] << " ";
}
quickSort(num, l, left - 1); //temp确定好了位置,把temp左面的数组和右面的数组分别进行这种方法排序
quickSort(num, left + 1, r); //当每个值的下标都确定的时候,该数组以完成排序
}

二路归并排序
思路:
二路归并,就是把一个数组,先分开,然后在合并的过程中逐步排序
二路就是分开的时候每次分成两个,分成两种路
归并就是把他分开在合上
二路分割数组,一直把数组分割到一路只有一个数为止
然后再把他们两路合一路,两路合一路,在合路的过程中把无序的路合成有序的路,慢慢的合成后的路都为有序的路,大致原理如下图

分路没有什么说的,一分为,对半分即可
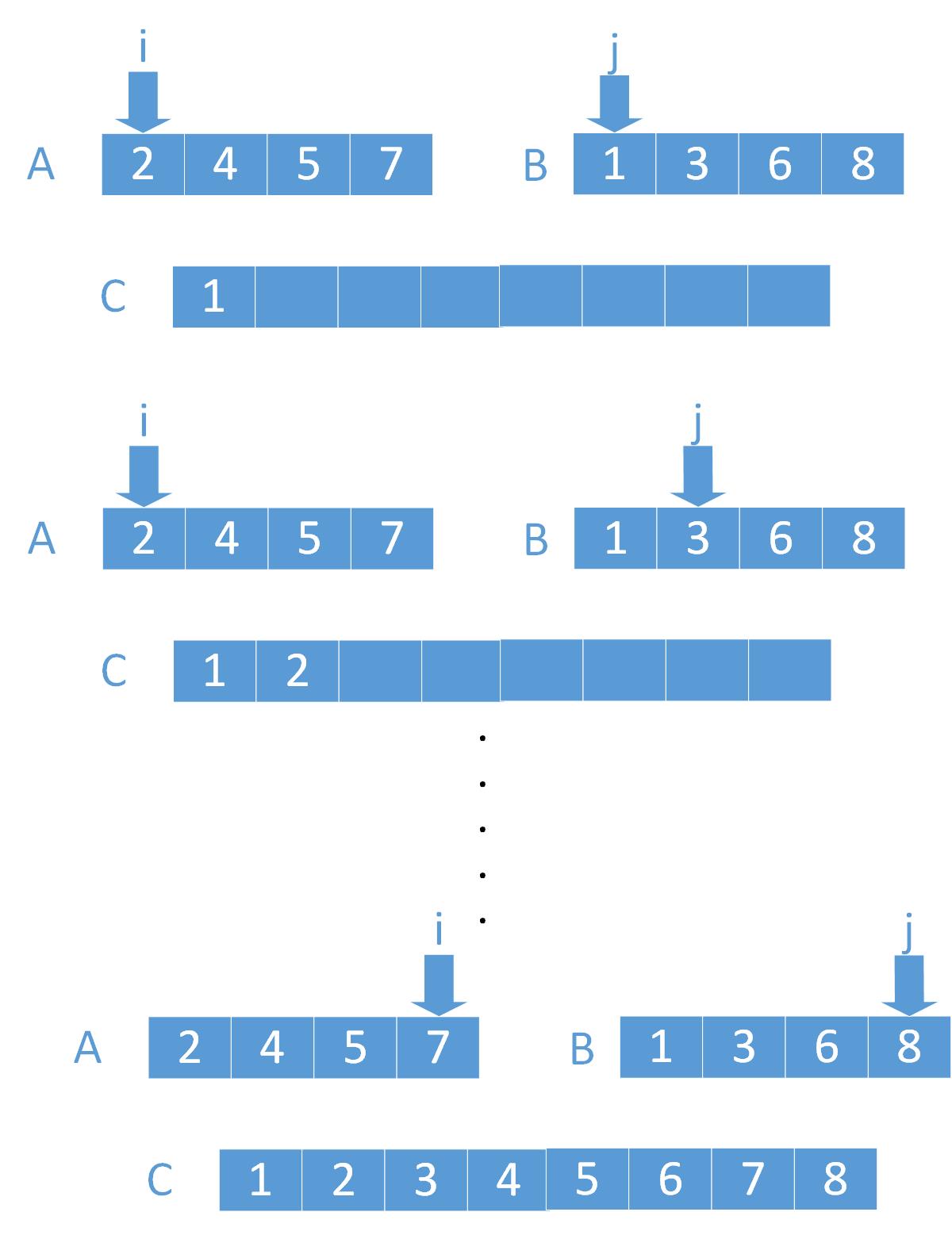
合路的时候,AB两个路合成C路,分别两个指针i,j,k对应着A,B,C数组的下标
循环AB两个数组,每次都比较A[i]与B[j] 取两个数组中对应值小的放到C[k]
然后k下标右移,i或者j小的下标右移,完全循环后,C==A+B的有序路
#include <iostream>
#include <vector>
using namespace std;
void mergeSort(vector<int> &num, int left, int right);
int m以上是关于2022计算机考研408—数据结构—排序的主要内容,如果未能解决你的问题,请参考以下文章