最长递增子序列的个数--了解两种实现LIS算法的区别

Posted 2021-10-09 C_YCBX Py_YYDS

文章目录

• • 题目
  • 题目解析
  • 解题代码

题目

oj平台

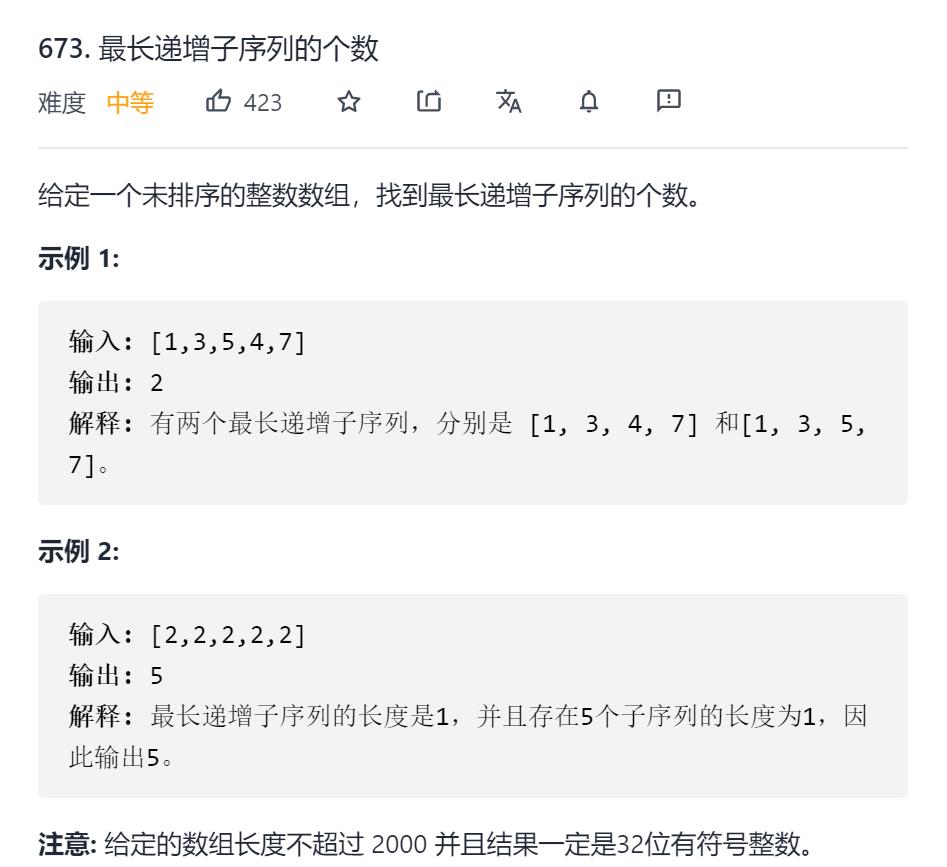
题目解析

说说我的心得吧。。

• 原本LIS的两种实现我是炉火纯青的，我一直想用二分的那个方法去dp得出最长递增子序列个数-----然后就折腾了一下午也没弄出来！（所以这里不会这种方法！）

• 但凡用两个for循环的那种方式更新dp也不至于这样😂，由于两个for循环的 dp[i] 表示以 i 下标结尾的最长递增子序列长度，而不是 0~i 中所有递增子序列的最长长度。

利用这个dp性质我们可很快构建出 cnt[i] 表示以 i 结尾最长递增子序列的个数，这个仅仅只需要在更新 dp 数组的时候进行判断更新 cnt 数组即可。

好了，接下来更新答案的过程就很简单了，利用 dp[i] 以及 cnt[i] 再加上一个辅助变量 mxLen 记录一下每次dp更新完后的最长子序列值即可。
（由于每个最长子序列都有它的结束下标，我们只需要通过 dp[i] 便可以将这些最长子序列都遍历完）

• 具体的部分代码：

if (dp[i] > mxLen) { //更新序列中的最长长度(更新过程--把res不断重置)
    mxLen = dp[i];
    res = cnt[i];
} else if (dp[i] == mxLen) { //得到多个最长长度(更新res)
    res += cnt[i];
}

解题代码

效率也不是很拉
C++代码

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
//由于这种直接两层循环找LIS的方式非常直接，所以用于寻找相同的数量的方式也就同样直接了，和Dijkstra的各种变式题的更新方式一致！
//@cnt[i] 记录以 i 结尾的最长递增序列的个数
//@dp[i]  这种非二分形式的dp，它并不是直接的0~i的最长递增序列长度，而是以i结尾的最长序列长度
//所以这种很好操作一个特定的序列数据(比如以i结尾的最长序列长度)
        int sz = nums.size();
        int dp[sz]; fill(dp,dp+sz,1);
        int cnt[sz]; fill(cnt,cnt+sz,1);
        int res = 0; //记录答案最长递增子序列的个数，需要用mxLen变量辅助更新(因dp[i]是以i结尾的限定原因) 
        int mxLen = 1;
        //i从0开始防止出现
        for(int i=0;i<sz;i++){
           //更新cnt数组和dp数组
            for(int j=i-1;j>=0;j--){
                if(nums[j]<nums[i]){ 
                    if(dp[j]+1>dp[i]){ //更新最长的子序列过程，需要把cnt不断重置
                        dp[i] = dp[j] + 1;
                        cnt[i] = cnt[j];
                    }
                    else if(dp[j]+1==dp[i]){
                        cnt[i] += cnt[j];
                    }
                }
            }
            if(dp[i]>mxLen){//更新序列中的最长长度(更新过程--把res不断重置)
                mxLen = dp[i];
                res = cnt[i];
            }else if(dp[i]==mxLen){//得到多个最长长度(更新res)
                res += cnt[i];
            }
        }
        return res;
    }
};

JAVA代码

class Solution {
    public int findNumberOfLIS(int[] nums) {
        int n = nums.length, maxLen = 0, ans = 0;
        int[] dp = new int[n];
        int[] cnt = new int[n];
        Arrays.fill(dp,1);
        Arrays.fill(cnt,1);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                if (nums[i] > nums[j]) {
                    if (dp[j] + 1 > dp[i]) {
                        dp[i] = dp[j] + 1;
                        cnt[i] = cnt[j]; // 重置计数
                    } else if (dp[j] + 1 == dp[i]) {
                        cnt[i] += cnt[j];
                    }
                }
            }
            if (dp[i] > maxLen) {
                maxLen = dp[i];
                ans = cnt[i]; // 重置计数
            } else if (dp[i] == maxLen) {
                ans += cnt[i];
            }
        }
        return ans;
    }
}