李宏毅机器学习误差梯度下降

Posted 2021-10-08 7TribeZ

Back to ML_Step 2 :define loss from training data

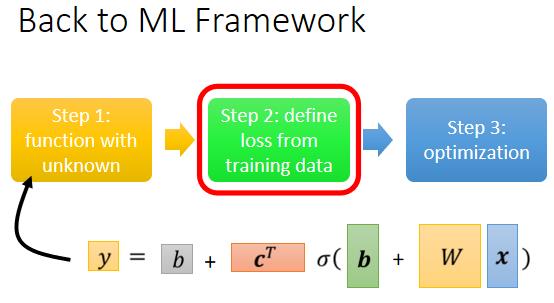
那接下来进入第二步了,我们要定 Loss,有了新的这个 Model 以后,我们 Loss 没有什麼不同,定义的方法是一样的,只是我们的符号改了一下,之前是 L ( w 跟 b ),因為 w 跟 b 是未知的,那我们现在接下来的未知的参数很多了,你再把它一个一个列出来,太累了,所以我们直接用 θ 来统设所有的参数,所以我们现在的 Loss Function 就变成

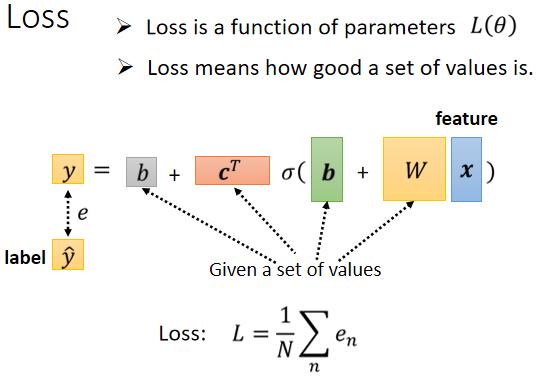
这个 Loss Function 要问的就是,这个 θ 如果它是某一组数值的话,会有多不好或有多好,那计算的方法,跟刚才只有两个参数的时候,其实是一模一样的

• 先给定某一组 跟 的值,你先给定某一组 的值,假设你知道 w 的值是多少,把 w 的值写进去 b 的值写进去,c 的值写进去 ,b 的值写进去
• 然后把一种 Feature x 带进去,然后看看你估测出来的 y 是多少
• 再计算一下跟真实的 Label 之间的差距,你得到一个 e
• 把所有的误差通通加起来,你就得到你的 Loss

Back to ML_Step 3: Optimization

接下来下一步就是 Optimization,Optimization跟前面讲的没有什麼不同 还是一样的,所以就算我们换了一个新的模型,这个 Optimization 的步骤.

我们现在的 θ 它是一个很长的向量,我们把它表示成 θ1 θ2 θ3 等等等,我们现在就是要找一组 θ,这个 θ 可以让我们的 Loss 越小越好,可以让 Loss 最小的那一组 θ,我们叫做 θ 的 Start

• 我们一开始要随机选一个初始的数值,这边叫做 你可以随机选,那之后也可能会讲,也会讲到更好的找初始值的方法,我们现在先随机选就好
• 接下来呢你要计算微分,你要对每一个未知的参数,这边用 θ1 θ2 θ3 来表示,你要為每一个未知的参数,都去计算它对 L 的微分,那把每一个参数都拿去计算对 L 的微分以后,集合起来它就是一个向量,那个向量我们用 g 来表示它,这边假设有 1000 个参数,这个向量的长度就是 1000,这个向量裡面就有 1000 个数字,这个东西有一个名字,,这个向量有一个名字叫做 Gradient,那很多时候你会看到,Gradient 的表示方法是这个样子的,你把 L 前面放了一个倒三角形,这个就代表了 Gradient,这是一个 Gradient 的简写的方法,那其实我要表示的就是这个向量,L 前面放一个倒三角形的意思就是,把所有的参数 θ1 θ2 θ3,通通拿去对 L 作微分.那后面放 θ0 的意思是说,我们这个算微分的位置,是在 θ 等於 θ0 的地方,在 θ 等於 θ0 的地方,我们算出这个 Gradient
• 算出这个 g 以后,接下来呢我们 Update 参数,更新的方法,跟刚才只有两个参数的状况是一模一样的,只是从更新两个参数,可能换成更新成 1000 个参数,但更新的方法是一样的,本来有一个参数叫 θ1,上标 0 代表它是一个起始的值,它是一个随机选的起始的值,把这个 减掉 η 乘上微分的值,得到 ,代表 θ1 更新过一次的结果, 减掉微分乘以,减掉 η 乘上微分的值,得到,以此类推,你就可以把那 1000 个参数统统都更新了.

简写把这边所有的 θ 合起来当做一个向量,我们用 来表示,把 η 提出来,那剩下每一个参数对 L 微分的部分,叫做 Gradient 叫做 g,所以 θ0 减掉 η 乘上 g,就得到 θ1

θ0 减掉 θ0 这个向量,减掉 η 乘上 g,g 也是一个向量会得到 θ1,那假设你这边参数有 1000 个,那 θ0 就是 1000 个数值,1000 微的向量,g 是1000 微的向量,θ1 也是 1000 微的向量

那整个操作就是这样了,就是由 θ0 算 Gradient,根据 Gradient 去把 θ0 更新成 θ1,然后呢再算一次 Gradient,然后呢根据 Gradient 把 θ1 再更新成 θ2,再算一次 Gradient 把 θ2 更新成 θ3,以此类推直到你不想做,或者是你算出来的这个 Gradient,是 0 向量 是 Zero Vector,导致你没有办法再更新参数為止,不过在实作上你几乎不太可能,作出 Gradient 是 0 向量的结果,通常你会停下来就是你不想做了.

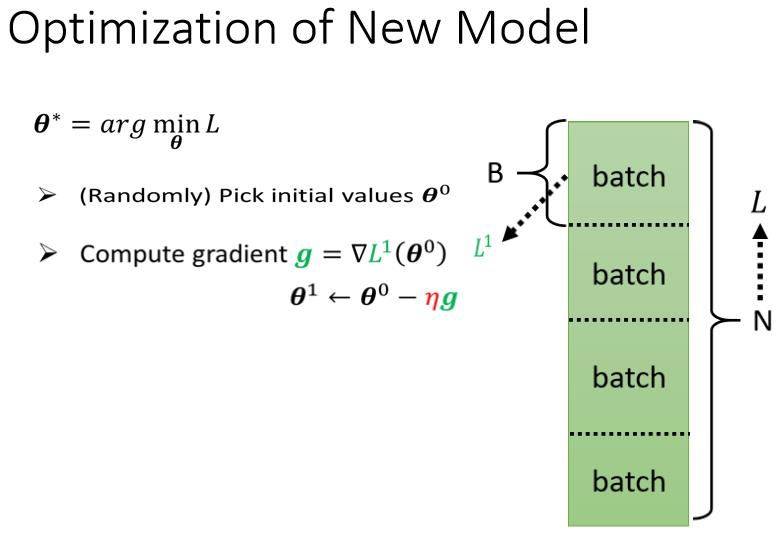
但是实作上,那这边是一个实作的 Detail 的 Issue,实际上我们在做 Gradient的时候,我们会这麼做

我们这边有大 N 笔资料,我们会把这大 N 笔资料分成一个一个的 Batch,就是一包一包的东西 一组一组的,怎麼分,随机分就好

所以每个 Batch 裡面有大 B 笔资料,所以本来全部有大 N 笔资料,现在大 B 笔资料一组,一组叫做 Batch

那本来我们是把所有的 Data 拿出来算一个 Loss,那现在我们不这麼做,我们只拿一个 Batch 裡面的 Data出来算一个 Loss,我们这边把它叫 L1,那跟这个 L 呢以示区别,因為你把全部的资料拿出来算 Loss,跟只拿一个 Batch 拿出来,的资料拿出来算 Loss,它不会一样嘛,所以这边用 L1 来表示它

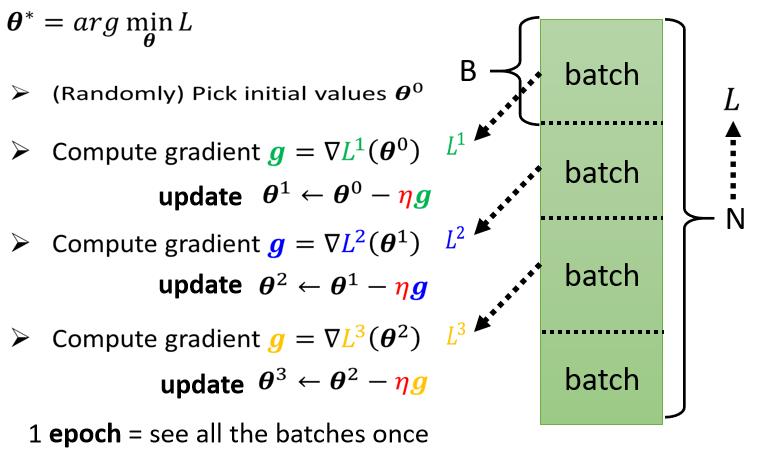
但是你可以想像说假设这个 B 够大,也许 L 跟 L1 会很接近 也说不定,所以实作上的时候,每次我们会先选一个 Batch,用这个 Batch 来算 L,根据这个 L1 来算 Gradient,用这个 Gradient 来更新参数,接下来再选下一个 Batch 算出 L2,根据 L2 算出 Gradient,然后再更新参数,再取下一个 Batch 算出 L3,根据 L3 算出 Gradient,再用 L3 算出来的 Gradient 来更新参数

所以我们并不是拿大 L 来算 Gradient,实际上我们是拿一个 Batch 算出来的 L1 L2 L3,来计算 Gradient,那把所有的 Batch 都看过一次,叫做一个 Epoch,每一次更新参数叫做一次 Update, Update 跟 Epoch 是不一样的东西

每次更新一次参数叫做一次 Update,把所有的 Batch 都看过一遍,叫做一个 Epoch

那至於為什麼要分一个一个 Batch,那这个我们下週再讲,但是為了让大家更清楚认识,Update 跟 Epoch 的差别,这边就举一个例子

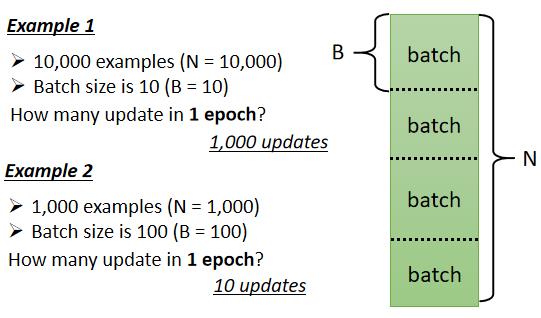
假设我们有 10000 笔 Data,也就是大 N 等於 10000,假设我们的 Batch 的大小是设 10,也就大 B 等於10

接下来问,我们在一个 Epoch 中,总共 Update 了几次参数?

那你就算一下这个大 N 个 Example,10000 笔 Example,总共形成了 10000 除以 10,也就是 1000 个 Batch,所以在一个 Epoch 裡面,你其实已经更新了参数 1000 次,所以一个 Epoch 并不是更新参数一次,在这个例子裡面一个 Epoch,已经更新了参数 1000 次了

那第二个例子,就是假设有 1000 个资料,Batch Size 设 100,那其实 Batch Size 的大小也是你自己决定的,所以这边我们又多了一个 HyperParameter,所谓 HyperParameter 就是你自己决定的东西,人所设的东西不是.机器自己找出来的,叫做 HyperParameter,我们今天已经听到了,几个 Sigmoid 也是一个 HyperParameters,Batch Size 也是一个 HyperParameter,好 1000 个 Example,Batch Size 设 100,那1个 Epoch 总共更新几次参数呢,是 10 次

所以做了一个 Epoch 的训练,你其实不知道它更新了几次参数,有可能 1000 次,也有可能 10 次,取决於它的 Batch Size 有多大

模型变型

那我们其实还可以对模型做更多的变形,刚才有同学问到说,这个 Hard Sigmoid 不好吗,為什麼我们一定要把它换成 Soft 的 Sigmoid

你确实可以不一定要换成 Soft 的 Sigmoid,有其他的做法,举例来说这个 Hard 的 Sigmoid,我刚才说它的函式有点难写出来,其实也没有那麼难写出来,它可以看作是两个 Rectified Linear Unit 的加总,所谓 Rectified Linear Unit 它就是长这个样

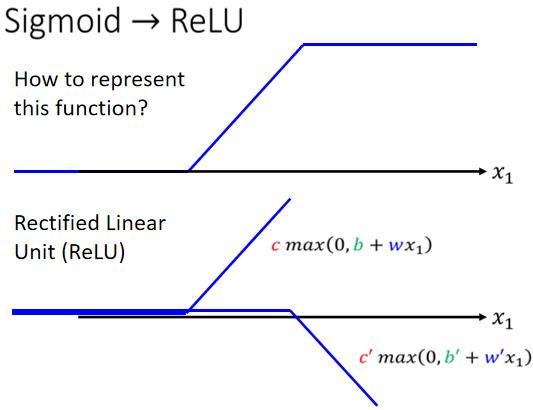
它有一个水平的线,走到某个地方有一个转折的点,然后变成一个斜坡,那这种 Function 它的式子,写成

这个的意思就是,看 0 跟 谁比较大,比较大的那一个就会被当做输出,所以如果 b + wx1 小於 0,那输出就是0,如果 大於 0,输出就是

那总之这一条线,可以写成,每条不同的 w 不同的 b 不同的 c,你就可以挪动它的位置,你就可以改变这条线的斜率,那这种线呢在机器学习裡面,我们叫做 Rectified Linear Unit,它的缩写叫做 ReLU,名字念起来蛮有趣的,它真的就唸ReLU

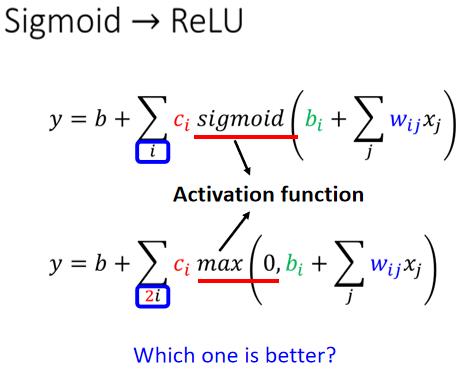
那你把两个 ReLU 叠起来,就可以变成 Hard 的 Sigmoid,你想要用 ReLU 的话,就把 Sigmoid 的地方,换成.

那本来这边只有 i 个 Sigmoid,你要 2 个 ReLU,才能够合成一个 Hard Sigmoid ,所以这边有 i 个 Sigmoid,那如果 ReLU 要做到一样的事情,那你可能需要 2 倍的 ReLU,因為 2 个 ReLU 合起来,才是一个 Hard Sigmoid,所以要 2 倍的 ReLU,所以我们把 Sigmoid 换成 ReLU,这边就是把一个式子换了,因為要表示一个 Hard 的 Sigmoid,表示那个蓝色的 Function 不是只有一种做法,你完全可以用其他的做法,好 那这个 Sigmoid 或是 ReLU,他们在机器学习裡面,我们就叫它 Activation Function,他们是有名字的,他们统称為 Activation Function.

当然还有其他常见的,还有其他的 Activation Function,但 Sigmoid 跟 ReLU,应该是今天最常见的 Activation Function,那哪一种比较好呢,这个我们下次再讲,哪一种比较好呢,我接下来的实验都选择用了 ReLU,显然 ReLU 比较好,至於它為什麼比较好,那就是下週的事情了.

接下来就真的做了这个实验,这个都是真实的数据.

• 如果是 Linear 的 Model,我们现在考虑 56 天,训练资料上面的 Loss 是 0.32k,没看过的资料 2021 年资料是 0.46k
• 如果用 10 个 ReLU,好像没有进步太多,这边跟用 Linear 是差不多的,所以看起来 10 个 ReLU 不太够
• 100 个 ReLU 就有显著的差别了,100 个 ReLU 在训练资料上的 Loss,就可以从 0.32k 降到 0.28k,有 100 个 ReLU,我们就可以製造比较复杂的曲线,本来 Linear 就是一直线,但是 100 个 ReLU 我们就可以產生 100 个,有 100 个折线的Function,在测试资料上也好了一些.
• 接下来换 1000 个 ReLU,1000 个 ReLU,在训练资料上 Loss 更低了一些,但是在没看过的资料上,看起来也没有太大的进步

多做几次

接下来还可以做什麼呢,我们还可以继续改我们的模型,

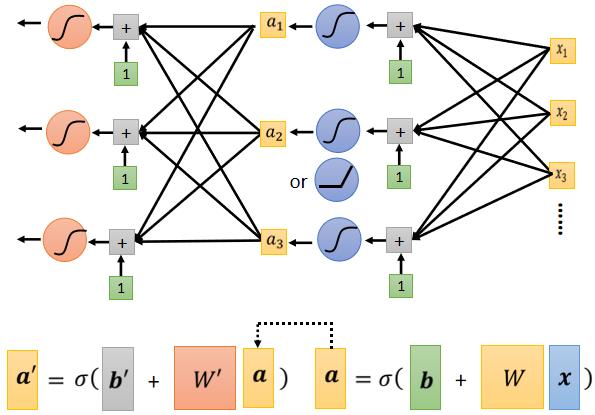
举例来说,刚才我们说从 x 到 a 做的事情,是把 x 乘上 w 加 b,再通过 Sigmoid Function,不过我们现在已经知道说,不一定要通过 Sigmoid Function,通过 ReLU 也可以,然后得到 a。

我们可以把这个同样的事情,再反覆地多做几次,刚才我们把 w x 乘上 w 加 b,通过 Sigmoid Function 得到 a,我们可以把 a 再乘上另外一个 w’,再加上另外一个 b’,再通过 Sigmoid Function,或 RuLU Function,得到 a’

所以我们可以把 x,做这一连串的运算產生 a,接下来把 a 做这一连串的运算產生 a’,那我们可以反覆地多做几次,要做几次,这个又是另外一个 Hyper Parameter,这是另外一个你要自己决定的事情,你要做两次吗 三次吗 四次吗 一百次吗,这个你自己决定,不过这边的 w 跟这边的 w’,它们不是同一个参数喔,这个 b 跟这边的 b’,它们不是同一个参数喔,是增加了更多的未知的参数

那就是接下来就真的做了实验了,我们就是每次都加 100 个 ReLU,那我们就是 Imput Features,就是 56 天前的资料

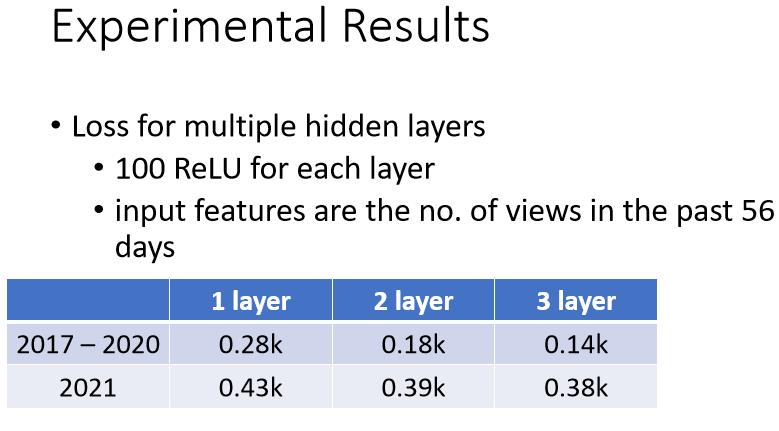
• 如果是只做一次 只做一次,就那个乘上 w 再加 b,再通过 ReLU 或 Sigmoid,这件事只做一次的话,这是我们刚才看到的结果
• 两次，这个 Loss 降低很多,0.28k 降到 0.18k,没看过的资料上也好了一些
• 三层，又有进步,从 0.18k 降到 0.14k,所以从一层到 从就是乘一次 w,到通过一次 ReLU,到通过三次 ReLU,我们可以从 0.28k 到 0.14k,在训练资料上,在没看过的资料上,从 0.43k 降到了 0.38k,看起来也是有一点进步的,