CF1253F Cheap Robot
Posted Jozky86
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CF1253F Cheap Robot相关的知识,希望对你有一定的参考价值。
题意:
给你一张 N 个点的带权无向连通图,其中结点 1,2,…,k 为充电中心。
一个机器人在图中行走,假设机器人的电池容量为 c,则任何时刻,机器人的电量 x 都必须满足 c0≤x≤c。如果机器人沿着一条边权为 w 的边从结点 i 走到结点 j,它的电量会减少 w。机器人可以在到达某个充电中心时把电量充满。
现在有 q 个询问,每次询问机器人要从 a 点到达 b 点,电池容量至少为多少,各个询问相互独立。保证 a 点和 b 点都是充电中心。
题解:
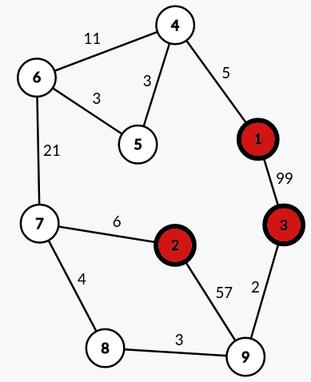
我和队友讨论这个题,讨论的大差不差,但是有个错误。我们一开始认为点a到点b的距离,直接跑最小生成树就可以,但其实并不是,我们忽略了充电中心的作用,比如从3到1,路线为3→9→8→7→2→7→6→5→4→1,到7时并没有直接前往6,而是先到2充满电,然后在去6,这样相当于及时充电。
也就是我们可以通过走向最近的充电中心来补充能量,这样可以优化电池容量,所以我们需要求出任意一个点到离他最近的充电站的距离
这怎么求?多源最短路,没必要,我们可以建一个超级源点,连向所有充电站,边权为0,然后再新图上跑一个最短路,求出所有点到离他最近的充电站的距离
现在得到dis[i]:表示距离点i最近的充电站的距离
怎么用呢?如下
对于一个可以完成的路径(不会在半路因为能量不足而无法完成)
我们设当前走到点i,剩余电量为x,一定会有
x
>
=
d
i
s
i
x>=dis_{i}
x>=disi(题目保证终点是充电站,且中途可以充电,如果x<dis_{i}就无法走到终点了)
设电容量为c,有
c
>
=
x
>
=
d
i
s
i
c>=x>=dis_{i}
c>=x>=disi,c相当于上界
因为走到i点至少要消耗
d
i
s
i
dis_{i}
disi的电(因为距离i最近的充电站才dis_{i},不可能总消耗比dis_{i}还小),所以有:
c
−
d
i
s
i
>
=
x
>
=
d
i
s
i
c-dis_{i}>=x>=dis_{i}
c−disi>=x>=disi
设下一个点是j,且边权为
w
i
j
wij
wij,有:
c
−
d
i
s
j
>
=
x
−
w
i
,
j
>
=
d
i
s
j
c-dis_{j}>=x-w_{i,j}>=dis_{j}
c−disj>=x−wi,j>=disj,道理同上(注意这个式子里的下标是j)
现在我们合并两个式子,就可以得到关于点i到点j的路径信息
有:
x
−
w
i
,
j
>
=
d
i
s
j
x-w_{i,j}>=dis_{j}
x−wi,j>=disj,我们用c来代替x,因为我们想要的是与c相关的式子,得到:
d
i
s
j
<
=
c
−
d
i
s
i
−
w
i
,
j
dis_{j}<=c-dis_{i}-w_{i,j}
disj<=c−disi−wi,j
整理:
c
>
=
d
i
s
i
+
d
i
s
j
+
w
i
,
j
c>=dis_{i}+dis_{j}+w_{i,j}
c>=disi+disj+wi,j
这个式子的含义不就是从点i到点j所需要的最小电池容量为
d
i
s
i
+
d
i
s
j
+
w
i
,
j
dis_{i}+dis_{j}+w_{i,j}
disi+disj+wi,j,也就是我们求出了原图中任意两个相邻点所需要的电池容量。
上述推到过程建议仔细阅读,慢慢体会,很妙
现在每次询问一个起点 a 到 b 的最小电池容量,就是找一条从 a 点到 b 点的路径,使得这个路径上的最大值最小
这个路径一定是在最小生成树上的,这是最小生成树经常解决的问题。因为最小生成树加边是从小到大,且保证图联通的情况下
我们构造最小生成树,然后问题就变成求a到b路径上的最大值,可以用LCA+倍增来求
这是一个综合性很强且考察代码能力的题,值得一刷
代码:
// Problem: F. Cheap Robot
// Contest: Codeforces - Codeforces Round #600 (Div. 2)
// URL: https://codeforces.com/contest/1253/problem/F
// Memory Limit: 512 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)
//#pragma GCC target("avx")
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast")
// created by myq
#include <algorithm>
#include <cctype>
#include <climits>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <list>
#include <map>
#include <queue>
#include <set>
#include <sstream>
#include <stack>
#include <string>
#include <unordered_map>
#include <unordered_set>
#include <vector>
using namespace std;
typedef long long ll;
#define x first
#define y second
typedef pair<ll,ll> pii;
const int N= 400010;
const int mod= 998244353;
inline int read()
{
int res= 0;
int f= 1;
char c= getchar();
while (c > '9' || c < '0') {
if (c == '-')
f= -1;
c= getchar();
}
while (c >= '0' && c <= '9') {
res= (res << 3) + (res << 1) + c - '0';
c= getchar();
}
return res;
}
struct node
{
int a;
int b;
ll c;
bool operator<(const node& w) const
{
return c < w.c;
}
} q[N];
int p[N];
vector<pii> v[N];
int idx;
int n, m, k, _;
int newcnt;
int val[N];
ll dist[N];
vector<pii> g[N];
vector<pair<int, ll>> ng[N];
int dep[N];
int f[N][20];
bool st[N];
ll f2[N][20];
int find(int x)
{
if (p[x] != x)
p[x]= find(p[x]);
return p[x];
}
// void dfs(int u,int fa,int top,ll sum=0){
// for(auto j:v[u]){
// if(j.x==fa) continue;
// if(j.x>k)
// dfs(j.x,u,top,sum+j.y);
// else
// {
// g[top].push_back({j.x,j.y});
// dfs(j.x,u,j.x,0);
// }
// }
// }
void dfs2(int u, int fa, ll faw)
{
dep[u]= dep[fa] + 1;
f[u][0]= fa;
f2[u][0]= faw;
for (auto j : ng[u]) {
if (j.x == fa)
continue;
dfs2(j.x, u, j.y);
}
}
ll maxlca(int a, int b)
{
ll maxv= 0;
if (dep[a] < dep[b])
swap(a, b);
for (int i= 19; i >= 0; i--)
if (dep[f[a][i]] >= dep[b]) {
maxv= max(maxv, f2[a][i]);
a= f[a][i];
}
if (a == b)
return maxv;
for (int i= 19; i >= 0; i--)
if (f[a][i] != f[b][i]) {
maxv= max(maxv, f2[a][i]);
maxv= max(maxv, f2[b][i]);
a= f[a][i], b= f[b][i];
}
maxv= max(maxv, max(f2[a][0], f2[b][0]));
return maxv;
}
void dijkstra()
{
priority_queue<pii, vector<pii>, greater<pii>> q;
for (int i= 0; i <= n; i++)
dist[i]= 1e18;
dist[0]= 0;
q.push({0, 0});
while (q.size()) {
auto tt= q.top();
q.pop();
if (st[tt.y])
continue;
st[tt.y]= 1;
for (auto j : g[tt.y]) {
if (dist[j.x] > dist[tt.y] + j.y) {
dist[j.x]= dist[tt.y] + j.y;
if (!st[j.x])
q.push({dist[j.x], j.x});
}
}
}
}
void init()
{
for (int i= 1; i <= 19; i++)
for (int u= 1; u <= n; u++) {
f[u][i]= f[f[u][i - 1]][i - 1], f2[u][i]= max(f2[u][i - 1], f2[f[u][i - 1]][i - 1]);
}
}
int main()
{
// ios::sync_with_stdio(0);
// cin.tie(0);
// cout.tie(0);
cin >> n >> m >> k >> _;
newcnt= k;
for (int i= 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
q[i]= {a, b以上是关于CF1253F Cheap Robot的主要内容,如果未能解决你的问题,请参考以下文章