干货分享 | 机器人学中的状态估计——学习笔记

Posted 2021-10-07 阿木实验室

最近学习了关于《机器人学中的状态估计》这本书，以下就是我对该本书的大致理解，和大家一起分享下学习经验。 以下文章干货内容较多，均是我的个人学习心得的分享，如有错误，还请大家指正。

1.基础概念 这本书可以说是SLAM入门系列神书之一，用深入浅出的言语告诉我们状态估计是怎么一回事。经过多年的发展，状态估计理论已经有了许多直接、重要的结果。比如卡尔曼滤波，最小二乘估计，最大后验估计等。这些结果在解决目标跟踪，定位，建图，轨迹融合等问题中占据着核心位置，并广泛应用于自动驾驶，机器人和无人机领域。那么什么是状态估计，状态估计就是理解传感器的本质。比如下图1就是典型的状态估计问题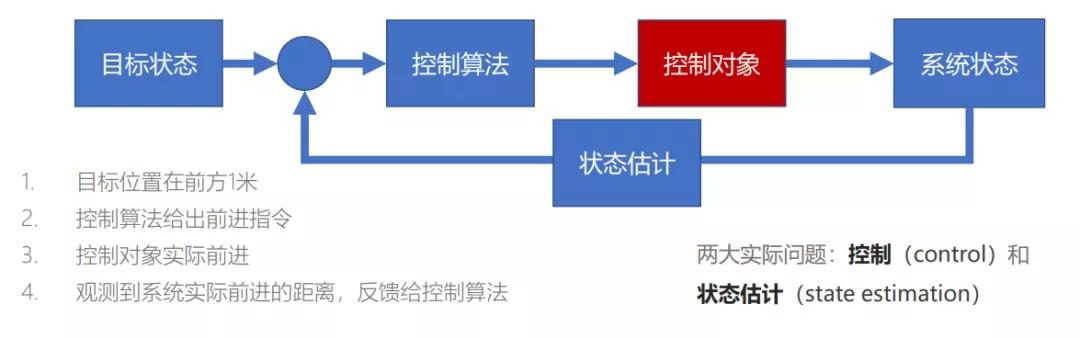： 图 1

但是，传感器的精度是有限的，如何利用传感器信息，尽可能准确的估计一组完整描述机器人随时间运动的物理量，如位置，速度，角度和角速度等，是状态估计领域要解决的最主要问题。因此，稳定，准确的状态估计是机器人稳定控制的必要基础。我们要知道SLAM问题的关键就是残差函数的最小二乘求解。“残差函数 = 测量值 – 估计值”，估计值就是我们根据传感器的模型去预估出来的。模型是好建立的，估计过程却是不好做的事情，需要考虑到噪声，偏置等其他不可估计量。尽管可以全部丢给后端优化，但是没有一个好的初值，后端优化可能会陷入局部最优，无法给到全局最优的结果。

2.重要概念 2.1 PDF函数和高斯分布 下面我们进入正题，首先这本书先介绍了PDF函数以及高斯分布下的线性变化后的均值和协方差如何变化，这里默认变量是二维。PDF在区间上积分就是概率。相信很多人一开始对先验概率，似然概率，后验概率没有很系统的认知，处于很懵的状态。那么我在这里就简单解释下，如果你对这些概率还是很模糊的话，那么就需要回去多看看书了。先验就是没有观测值的概率分布，也可以理解为初始值。似然就是观测的概率分布，后验估计就是加入观测后的概率分布，可以看作是对先验估计的矫正。

接下来就是条件概率，联合概率以及大名鼎鼎的贝叶斯公式。这里简单解释下条件概率，例如p(x|y),就是x在y的条件下发生的概率是多少。我们可以把y看作是条件。举一个很简单的例子，明天下雨的概率是多少。条件y是明天，要求的x是下雨的概率。

贝叶斯公式：联合 = 条件 * 边缘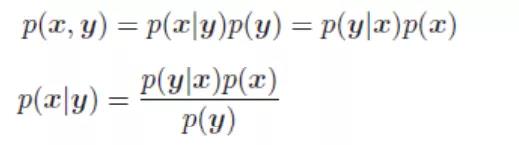

赋予该式物理意义：x = 状态,y = 传感器读数,p(y|x) = 传感器模型,p(x|y) = 状态估计。

上式可以说是本书最重要的内容之一，很多内容都会涉及到这里。

2.2 LG和MAP 然后带我们了解了LG和NLNG系统的区别以及有什么不同的处理方式。提到LG系统怎么能不提MAP方法，作为一种离散时间的批量估计方法，最大后验估计(MAP)无疑是最直观的。最大后验估计顾名思义，已知测量和输入的情况下，怎么才能估计出下一时刻最优值。下式先根据贝叶斯公式做了变形。由于分母和无关，直接舍去。

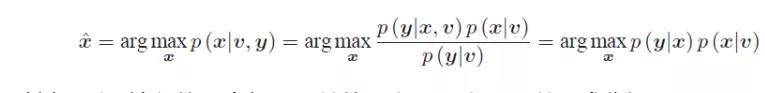下图是取完对数的情况，由于各时刻，输入的噪声都是无关的，上面两个项可以因式分解。然后求最小二乘的解就是我们要的最优解。我们把第一个时刻的先验提取出来，单独作用于第一个的估计。 推导完了批量MAP，接下来就是递归平滑算法，由于篇幅受限，我们就不再赘叙了，我们只需要知道递归的算法流程等价于传统的RTS平滑算法，五个前向的迭代等价于著名的卡尔曼滤波器。本书中对于卡尔曼滤波的推导，让我打开了新的思路，原来卡尔曼还可以这么推导。几种扩展卡尔曼滤波的介绍，也给我提供了更多的思路。尽管公式繁杂，但是一步一个脚印的推导过来，你会发现是一件很有成就的事情。

2.3NLNG和EKF 在接下来，就是NLNG系统，可以说LG系统过于理想化，现实生活中基本不存在这样的模型，无论什么样的系统都会有噪声。那么卡尔曼滤波都失效了，有什么好的方法呢？大牛们就提出了EKF，可以用来处理非线性模型。

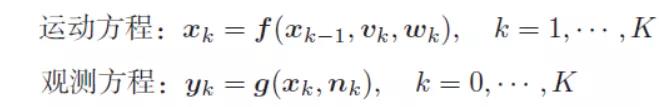
EKF同时还假设了马尔可夫性，给定现在时刻的状态时，未来时刻状态与过去时刻是条件独立的。那么就可以根据递归来估计最新时刻的估计值。下式中，我们把最新的观测分离出来。 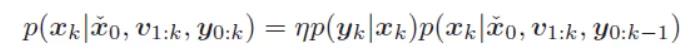右式第一项比较好处理，第二项则需要引入k-1时刻的状态。由于马尔科夫性，不必在引入k-1时刻之前的内容。 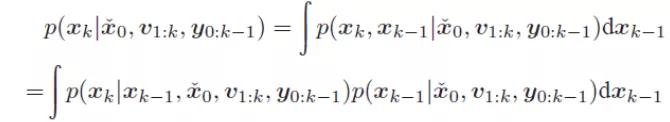因为篇幅有限，接下来的推导就不做展开，不做推导，感兴趣的同学可以自己尝试推一推。

2.4四元数和欧拉角 后面几章的三维刚体变化以及李群李代数也是SLAM的基础知识，学完这些，你需要知道什么是欧拉角，四元数，反对称矩阵以及归一化后的变换矩阵之间的转换关系。四元数的叉乘，点乘以及几种常用的公式，都是需要掌握的。这里具体的公式大家可以自行上网查找。

2.5李群李代数 对于李群和李代数，大家需要知道李群和李代数之间的转换关系，指数映射和对数映射是谁对谁，在球面上是不是满射。在SLAM问题中，位姿是未知的，而我们需要解决“什么样的相机位姿符合当前观测数据”。如前所言，旋转矩阵是带有约束的，行列式为1且为正交矩阵。作为变量带入BA中，无疑会增加难度。李代数我们在求解最小二乘问题，提供无约束的变量，可以减少BA维护维度。还有李代数的右乘和左乘扰动模型，对于我们求微小量有很大的帮助。李代数和李群还有许多性质，这里说不完，等待大家自己去发现。

3.结束语 写在最后，世上无难事，只怕肯攀登。确实，学习本就是个累积的过程。不积跬步无以至千里，不积小流无以至江海。可能这条道路上充满了挑战和未知，但是面对未知的挑战，大家应该感觉到兴奋，因为人类就喜欢在未知的领域中迎接挑战，不要害怕，公式和代码不过是纸老虎而已。一遍不行，那就三遍。慢慢的你就会发现，你对纸老虎的害怕早就荡然无存，更何况我们还是站在巨人的肩膀上。加油吧，同学们，SLAM的路虽然艰苦但是很有趣。

关注阿木实验室GZH，后台回复：“机器人学习” 可领取免费学习资料！

这世上所有好走的路都是下坡路，努力上坡！写给诸君共勉。

• End -

技术发展的日新月异，阿木实验室将紧跟技术的脚步，不断把机器人行业最新的技术和硬件推荐给大家。看到经过我们培训的学员在技术上突飞猛进，是我们培训最大的价值。如果你在机器人行业，就请关注我们的公众号，我们将持续发布机器人行业最有价值的信息和技术。

阿木实验室致力于前沿IT科技的教育和智能装备，让机器人研发更高效！