常见排序之近线性排序

Posted 2021-10-07 捕获一只小肚皮

文章目录

• 前言
• 堆排序
• 快速排序
• 归并排序
• 希尔排序

前言

上一章节,博主讲述了时间复杂度为O(n²)的排序算法,今天博主要介绍的主要是四个 堆排序,快排,归并排序和希尔排序,他们的共同点是,前三者的时间复杂度为O(n*logn),后面为O(n^1.3),都是接近线性的复杂度.

堆排序

堆排序的内容博主在讲解二叉树部分时候就已经详细阐述了

所以,为了方便,这里就直接放链接了堆排序

快速排序

在讲解快速排序之前,我们先做一个荷兰国旗问题

荷兰国旗问题:

有一无序数组,要求把数组划分成三个区域,左边区域小于某个值,中间区域等于某个值,右边区域大于某个值

示例1

输入:

[6,2,4,9,8,5,7,5,3,6,5,7,8,5,9];
k = 5;

输出:

[2,4,3,5,5,5,5,7,6,8,7,8,9,9,6]

可以清晰的看到,小于5的在左边,等于5的在中间,大于5的在右边.

算法实现:

• 初始化小于区域less<=-1,大于区域more>=n
• 设置当前指针cur,从索引0开始出发.
• 如果cur指向的值小于k,则cur的值和less下一个值交换,然后less++,cur++;
• 如果cur指向的值等于k,啥都不管,cur++;
• 如果cur指向的值大于k,则cur的值和more前一个值交换,然后more++,cur不变,为什么不变?因为和more区域前一个交换后,cur指向的值仍可能大于k.;

图解:

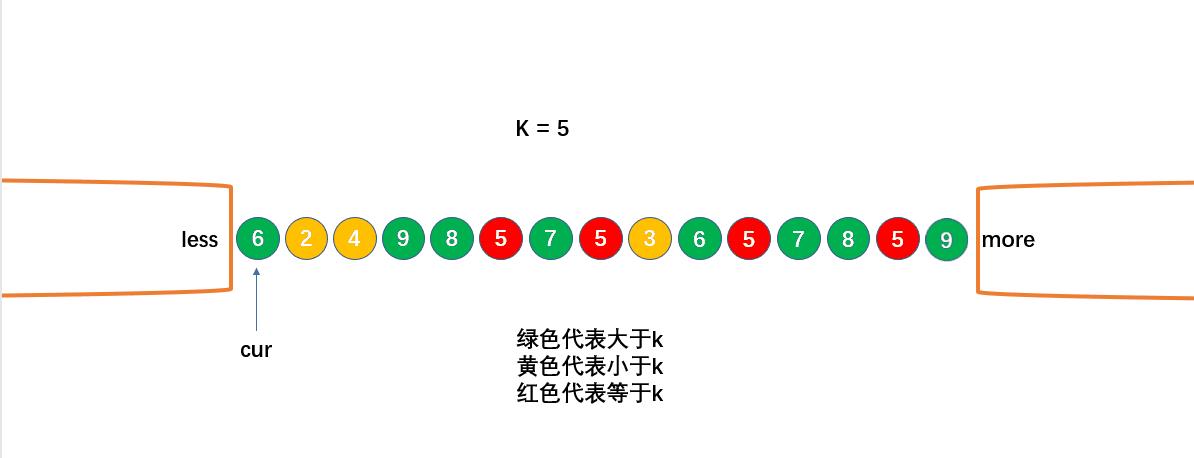
所以代码为:

int less = -1,more = n,cur = 0,k = 5;
while(cur<more)
{
    if(num[cur] < k) swap(&num[cur++],&num[++less]); //如果小于k,就和less下一个位置交换,然后less加加,cur加加
    else if(num[cur] > k) swap(&num[cur],&num[--more]);//如果大于k,就和more前一个位置交换,然后more减减,cur不变
    else cur++; //如果等于k,啥都不管,cur后移
}

既然荷兰国旗问题已经解决,那么快速排序代码怎么些呢?

我们知道荷兰国旗问题完成一次后,左边是小于k的,右边是大于k的,中间等于k,那么说明中间已经有序,则不需要再管理,相反,所需要排序的部分是less区域和more区域.

所以,快速排序内容就是,先执行一次荷兰国旗问题,然后继续递归排序less区域和more区域,只是k值是我们选择

其中,如果数组元素只剩下一个,则说明不需要排序

void QuickSort(int num[],int l,int r)  //l是数组左边区域,r是数组右边区域
{
    if(l>=r) return ;
    
    int less = l-1,more = r+1,cur = l,k = num[(l+r)>>1]; //选中间的为k值 (l+r)>>1等价于(l+r)/2
 
    while(cur<more)
    {
        if(num[cur] < k) swap(&num[cur++],&num[++less]); //如果小于k,就和less下一个位置交换,然后less加加,cur加加
        else if(num[cur] > k) swap(&num[cur],&num[--more]);//如果大于k,就和more前一个位置交换,然后more减减,cur不变
        else cur++; //如果等于k,啥都不管,cur后移
    }
    
    QuickSort(num,l,less);  //对l到less区域再进行荷兰国旗问题
    QuickSort(num,more,r);  //对more到r区域再进行荷兰国旗问题
}

测试:

---

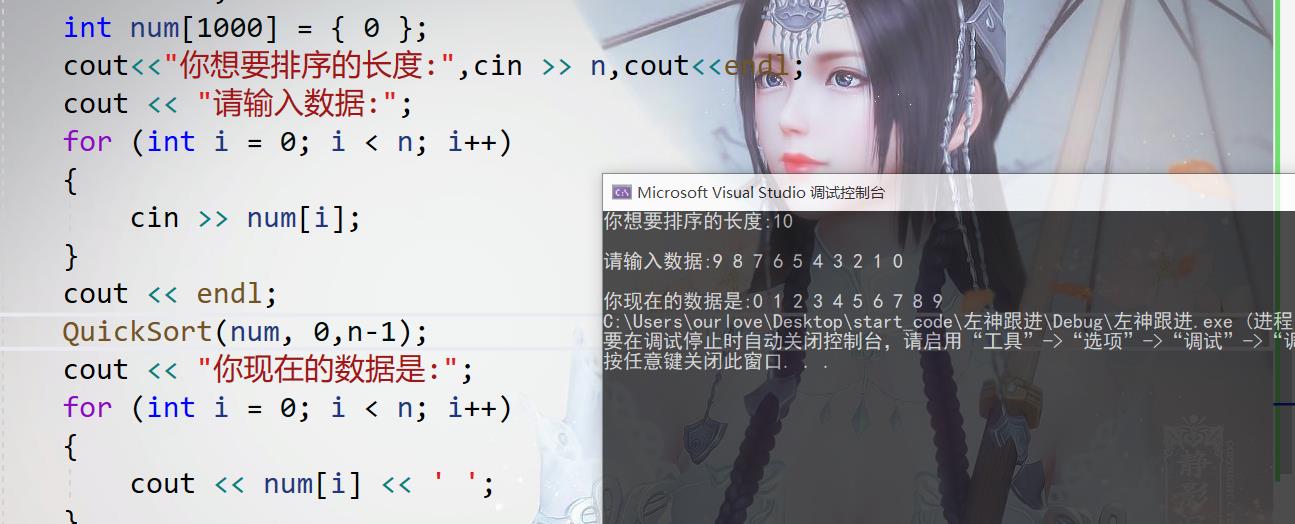
归并排序

归并排序的思想是,把数组分成两份,对左边排序,然后对右边排序,然后比较已排序左右两边的数,按照大小依次放到临时数组里面,然后放回原数组.

下面是归并动图(即对已有顺序数组,比较左右两边大小,放入临时数组,然后返回原数组),其步骤是:

• 对于左边部分用一个指针从头开始指向(l)
• 对于右边部分用一个指针从头开始指向®
• 如果左边arr[l]小于等于右边arr[r],把左边arr[l]放入临时数组,然后l++
• 如果左边arr[l]大于右边arr[r],把右边arr[r]放入临时数组,然后r++
• 如果l或者r走到边界,就停止,然后依次检查哪部分还有剩余的元素,全部放进临时数组

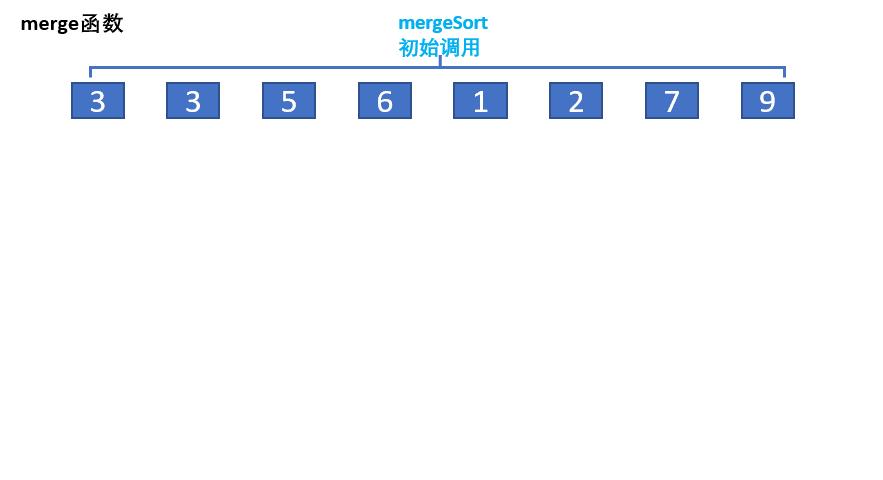
上面动图的前提是左右部分有序,那怎么让左右部分有序呢?

如果只有两个数据,左边一个,右边一个,可不可以认为左右两边分别有序?

然后我们按照上图思路归并两个元素,对于整个数组来说,我们先拆分,然后归并,那么整体就变成有序,如下图

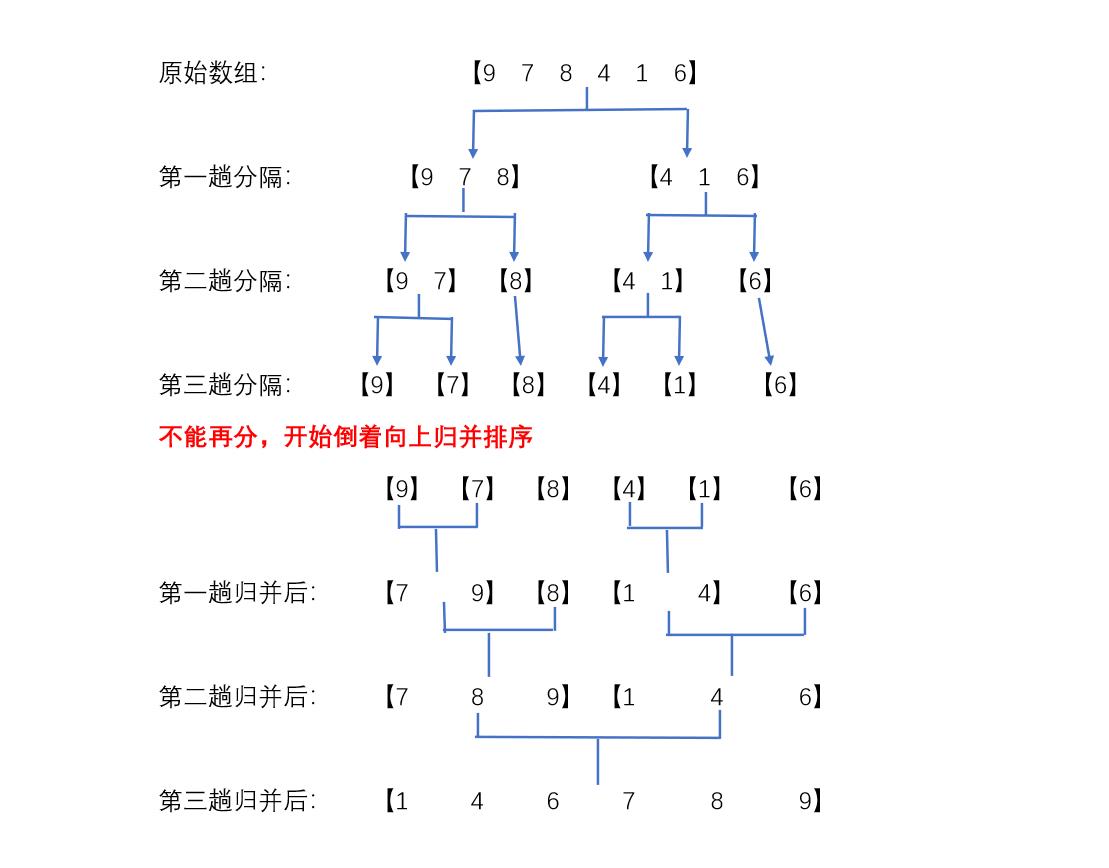
代码该怎样写呢?我们从简到繁,先写归并代码,按照归并步骤,代码如下:

int tmp[1000] = {0}
int i,j,k,mid;
mid  = (l+r)>>1;
//由于原数组是先被划分两半,然后再归并的,所以mid是左右数组分界线,即mid是原数组的中点
for(i = l,j = mid + 1,k = 0;i<=mid && j<=r;k++)   //无论是左边还是右边,一方走到边界,就停止
{
    if(num[i]<=num[j]) tmp[k] = num[i++]; //左边小于右边,把num[i]放进tmp数组,然后i++
    else tmp[k] = num[j++];               //左边大于右边,把num[j]放进tmp数组,然后j++
}

while(i<=mid) tmp[k++] = num[i++];  //如果右边先到边界,左边还有剩余,则依次全部放进tmp数组

while(j<=r) tmp[k++] = num[j++];  //如果左边先到边界,右边还有剩余,则依次全部放进tmp数组

for(i = 0,j = l;i<k;i++,j++) num[j] = tmp[i];      //把临时数组的值放回原数组

归并代码我们已经写出来了,那么归并排序呢?其实博主上面就已经说了,归并排序其实不存在排序这一说法,其之所以会有序,是因为我们在递归划分数组时候,最终一定会划分为左边和右边都只有一个数的情况,这时候归并就开始发挥作用,等此层递归结束,就会返回到上层递归,上层就不是左右只有一个数了,而是左右有两个数,但是在之前左右两个数由于归并已经有序,所以再次归并,周而复始…最后有序,就如上图,所以我们可以得出结论:归并排序并未排序,核心只是不断向下划分区域,到达底线后,不断向上归并,最终有序.

递归划分代码:

void MergeSort(int num[],int l,int r)
{
    if(l>=r) return ;             //如果只剩下一个元素,停止递归划分,返回上一层递归
    
    int mid = (l+r)>>1;           //先对原数组左右划分成两份
    MergeSort(num,l,mid);         //对划分后的左数组(l到mid区域),在进行同样划分
    MergeSort(num,mid+1,r);       //对划分后的右数组(mid+1到r区域),在进行同样划分
    
    //大家看递归的时候,一定要弄清楚递归定义,比如MergeSort,就是划分区域,逐渐返回的时候形成有序.
    //所以上面对左右两边划分区域后,左右已经有序.下面我们就进行归并
    int i = 0,j = 0,k = 0;    
    int tmp[1000] = {0};
    for(i = l,j = mid + 1,k = 0;i<=mid && j<=r;k++)   //无论是左边还是右边,一方走到边界,就停止
    {
        if(num[i]<=num[j]) tmp[k] = num[i++]; //左边小于右边,把num[i]放进tmp数组,然后i++
        else tmp[k] = num[j++];               //左边大于右边,把num[j]放进tmp数组,然后j++
    }
    while(i<=mid) tmp[k++] = num[i++];  //如果右边先到边界,左边还有剩余,则依次全部放进tmp数组
    while(j<=r) tmp[k++] = num[j++];  //如果左边先到边界,右边还有剩余,则依次全部放进tmp数组
    for(i = 0,j = l;i<k;i++,j++) num[j] = tmp[i];      //把临时数组的值放回原数组
}

测试:

---

希尔排序

希尔排序是进阶版本的插入排序,我们先回顾下插入排序适合哪种数据进行排序?答案是数据部分有序,而希尔排序的过程是,在插入排序之前进行一部分调整,让数据尽可能的达到部分有序.

那么是怎么让数据部分有序的呢?这就是一个牛逼的人–希尔想出来的.他把数据间隔成多块,举例为gap,然后按照gap距离进行插入排序.

比如有数据[9,8,7,6,5,4,3,2,1,5,4,3],我们用3个数据距离进行划分,然后依次插入排序,如下图:

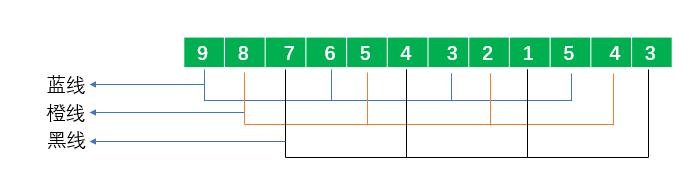
• 对于蓝线来说,其上的数据有9 6 3 5,这4个数据进行排序后为3 5 6 9,原数据变成[3 8 7 5 5 4 6 2 1 9 4 3]
• 对于橙线来说,其上的数据有8 5 2 4,这4个数据进行排序后为2 4 5 8,原数据变成[3 2 7 5 4 4 6 5 1 9 8 3]
• 对于黑线来说,其上的数据有7 4 1 3,这4个数据进行排序后为1 3 4 7,原数据变成[3 2 1 5 4 3 6 5 4 9 8 7]

可以看见,数据已经部分有序 3 2 1 5 4 3 6 5 4 9 8 7

而倘若我们继续把gap变成2,然后仍然进行相关操作,最后gap变成1,也就是真的插入排序,这些整个操作合在一起就是希尔排序

写任何一段代码,我们都应该遵循从简到繁,所以希尔排序的内容比较简单的步骤是什么呢? 没错,就是相隔gap距离的数据进行排序

按照上面的步骤我们是先让**整个蓝线有序,然后橙线,最后黑线,**但是这样写代码将会是一个及其耗费时间和精力的工作,其实我们可以更换一个简单的思路,最后也可以进行达到上述效果,那思路是什么呢?

我们直接挨着数组进行遍历,然后交换gap距离的数,什么意思呢?

• 我们直接从蓝线的第二个数据(索引为gap)开始,也就是6,然后6和蓝线上的第一个数据交换,变成6 9
• 紧接着我们从橙线的第二个数据(索引为gap+1)开始,也就是5,然后5和橙线的第一个数据交换,变成 5 8
• 紧接着我们从黑线的第二个数据(索引为gap+2)开始,也就是4,然后4和黑线的第一个数据交换,变成4 7
• 然后又从蓝线的第三个数据开始,也就是3,然后3和蓝线的前两个数据排序,变成3 6 9…
• 然后又从橙线的第三个数据开始,也就是2,然后2和橙线的前两个数据排序,变成2 5 8…
• 然后又从黑线的第三个数据开始,也就是2,然后1和黑线的前两个数据排序,变成1 4 7…

也就是我们直接从索引gap处开始,然后向后遍历,在遍历的过程中,进行相隔距离gap的数据排序,而这个过程所操作的一直在循环蓝线橙线黑线,又蓝线橙线黑线...进而达到了先整体蓝线,整体橙线,整体黑线的效果.

同理,写代码怎么写呢?我们还是从简到繁,先给gap赋一个值,以3为例.

int gap = 3;
for(int i = gap;i<n;i++)
{
    int min_index = i;
    int target = num[i];
    for(int j = i;j>=0;j-=gap)    //插入是按照gap距离来算的,所以j-=gap
    {
        if(num[j] < num[j-gap]) num[j] = num[j-gap],min_index = j-gap; //这里和插入排序一样,只是插入排序减去的是1
    }
	num[min_index] = target;      //插入到正确位置.
}

既然最简单的步骤写完以后,那么我们开始进行完整的希尔排序代码了,既然说希尔是进阶版本的插入排序,那么希尔的核心在哪里呢?没错,核心就是gap的取值,因为我们要保证预处理一部分值以后,最后进行真正的插入排序,即gap等于1,那么gap的值该怎样取呢?这就感谢我们的前辈们辛苦努力了,他们经过大量实验得出gap取值最好用 gap = gap/3+1

所以完整的希尔代码如下:

void ShellSort(int num[],int n)
{
    int  gap = n;
    while(gap>1)
    {
        gap = gap/3 + 1;
        for(int i = gap;i<n;i++)
        {
            int min_index = i;
            int target = num[i];
            for(int j = i;j>=gap;j-=gap)    //插入是按照gap距离来算的,所以j-=gap,之所以j>=gap因为j-gap不可越界
            {
                if(target < num[j-gap]) 
                    num[j] = num[j-gap],min_index = j-gap; //这里和插入排序一样,只是插入排序减去的是1
            }
            num[min_index] = target;      //插入到正确位置.
        }
    }
}

测试: