PCL：主成分分析（PCA）原理与实现

Posted 2021-10-05 没事就要敲代码

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了PCL：主成分分析（PCA）原理与实现相关的知识，希望对你有一定的参考价值。

文章目录

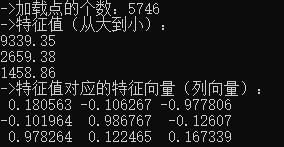
结果预览：

1 PCA 原理

2 代码实现

#include <pcl/io/pcd_io.h>
#include <pcl/common/pca.h>

using namespace std;

typedef pcl::PointXYZ PointT;

int main()
{
	//------------------------------ 加载点云 -----------------------------------
	pcl::PointCloud<PointT>::Ptr cloud(new pcl::PointCloud<PointT>);
	if (pcl::io::loadPCDFile("tree.pcd", *cloud) < 0)
	{
		PCL_ERROR("\\a点云文件不存在！\\n");
		system("pause");
		return -1;
	}
	cout << "->加载点的个数：" << cloud->points.size() << endl;
	//==========================================================================

	//---------------------------------- PCA -----------------------------------
	pcl::PCA<PointT> pca;			//创建pca对象
	pca.setInputCloud(cloud);		//设置输入点云
	size_t row_start = 0;			//感兴趣区域的起始行数
	size_t col_start = 0;			//感兴趣区域的起始列数
	size_t nb_rows = cloud->height;	//总行数
	size_t nb_cols = cloud->width;	//总列数
	pca.setIndices(row_start, col_start, nb_rows, nb_cols);	//设置感兴趣区域点云的索引
	cout << "->特征值（从大到小）：\\n" << pca.getEigenValues() << endl;
	cout << "->特征值对应的特征向量（列向量）：\\n" << pca.getEigenVectors() << endl;
	//==========================================================================

	return 0;
}

3 输出结果

->加载点的个数：5746
->特征值（从大到小）：
9339.35
2659.38
1458.86
->特征值对应的特征向量（列向量）：
 0.180563 -0.106267 -0.977806
-0.101964  0.986767  -0.12607
 0.978264  0.122465  0.167339

4 PCL源码

4.1 setIndices()

template <typename PointT> void
pcl::PCLBase<PointT>::setIndices (size_t row_start, size_t col_start, size_t nb_rows, size_t nb_cols)
{
  if ((nb_rows > input_->height) || (row_start > input_->height))
  {
    PCL_ERROR ("[PCLBase::setIndices] cloud is only %d height", input_->height);
    return;
  }

  if ((nb_cols > input_->width) || (col_start > input_->width))
  {
    PCL_ERROR ("[PCLBase::setIndices] cloud is only %d width", input_->width);
    return;
  }

  size_t row_end = row_start + nb_rows;
  if (row_end > input_->height)
  {
    PCL_ERROR ("[PCLBase::setIndices] %d is out of rows range %d", row_end, input_->height);
    return;
  }

  size_t col_end = col_start + nb_cols;
  if (col_end > input_->width)
  {
    PCL_ERROR ("[PCLBase::setIndices] %d is out of columns range %d", col_end, input_->width);
    return;
  }

  indices_.reset (new std::vector<int>);
  indices_->reserve (nb_cols * nb_rows);
  for(size_t i = row_start; i < row_end; i++)
    for(size_t j = col_start; j < col_end; j++)
      indices_->push_back (static_cast<int> ((i * input_->width) + j));
  fake_indices_ = false;
  use_indices_  = true;
}

4.2 initCompute()

template<typename PointT> bool
pcl::PCA<PointT>::initCompute () 
{
  if(!Base::initCompute ())
  {
    PCL_THROW_EXCEPTION (InitFailedException, "[pcl::PCA::initCompute] failed");
    return (false);
  }
  if(indices_->size () < 3)
  {
    PCL_THROW_EXCEPTION (InitFailedException, "[pcl::PCA::initCompute] number of points < 3");
    return (false);
  }
  
  // Compute mean
  mean_ = Eigen::Vector4f::Zero ();
  compute3DCentroid (*input_, *indices_, mean_);  
  // Compute demeanished cloud
  Eigen::MatrixXf cloud_demean;
  demeanPointCloud (*input_, *indices_, mean_, cloud_demean);
  assert (cloud_demean.cols () == int (indices_->size ()));
  // Compute the product cloud_demean * cloud_demean^T
  Eigen::Matrix3f alpha = static_cast<Eigen::Matrix3f> (cloud_demean.topRows<3> () * cloud_demean.topRows<3> ().transpose ());
  
  // Compute eigen vectors and values
  Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> evd (alpha);
  // Organize eigenvectors and eigenvalues in ascendent order
  for (int i = 0; i < 3; ++i)
  {
    eigenvalues_[i] = evd.eigenvalues () [2-i];
    eigenvectors_.col (i) = evd.eigenvectors ().col (2-i);
  }
  // If not basis only then compute the coefficients

  if (!basis_only_)
    coefficients_ = eigenvectors_.transpose() * cloud_demean.topRows<3> ();
  compute_done_ = true;
  return (true);
}