rsa加密算法简单介绍
Posted Nullan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了rsa加密算法简单介绍相关的知识,希望对你有一定的参考价值。
前言
聊天工具发送文字,表情包,一笔付款,怎么保证对方接受的信息与自己发送的信息保持一致,中间没有进行修改,答案就是对发送的信息进行信息加密与签名,并在接收端进行校验与解密。
密码学基础
对称加密
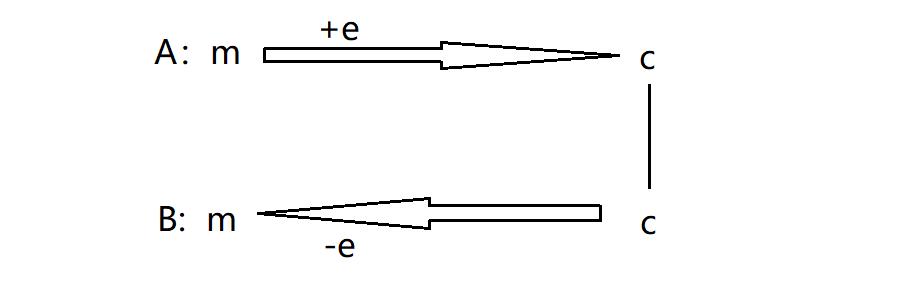
此时,m称为明文,就是我们希望表达的含义
C我们称为密文,我们可以公开传递的信息
而e就是密钥,不能告诉其他人,这个e的算法可以有很多种
但是算法再复杂也会被破解,因为可以穷举,尝试以前的算法,也可以通过频率,比如26个字母里,在一段话频率不一样,截取多种密文,可以试出来
如果发一段话换一个密钥呢?密钥的分发又成了一个问题。但是现在的量子保密通信就可以实现密钥分发的保密性
非对称加密
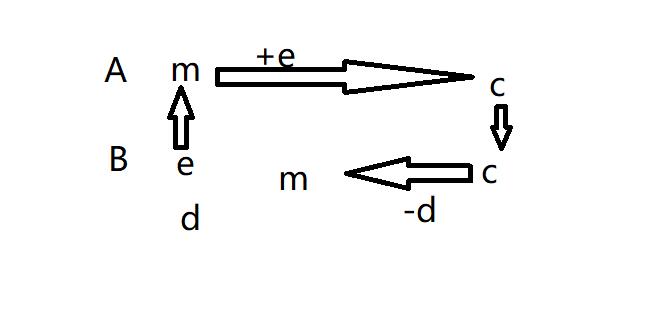
A发给B,但是B生成两个有相互关系的数字,e和d,e叫做公钥,公共的钥匙,d叫做私钥,私人的钥匙,B先把e传给A,可以以公开方式进行传递。A通过公钥的某一种算法,得到一个密文c,然后再把这个C给到B,然后用私钥解密得到m,得到公钥仍然无法得到明文,这就是非对称加密的方式
RSA加密算法
简单介绍
MIT三位数学教授于1978年发明的一种算法
1.先让B找出两个质数,一个叫P,一个叫Q(质数:只有1和它本身两个约数的数叫做质数)
2.做一个乘法 n = pq做个乘法
3.取一个函数为 φ(n) = (p-1)(q-1) 欧拉函数
4.公钥e 1< e <φ(n) 的一个整数 ,且e和 φ(n)必须要互质(两个没有公共因子)
5.私钥d 满足e*d/ φ(n)的余数为1 ,这个d称为e关于φ(n)的模逆元记为
e
d
≡
1
(
m
o
d
φ
(
n
)
)
ed\\equiv 1(mod\\ \\varphi(n) )
ed≡1(mod φ(n))
例:
φ(n) = 20,e = 3 ,求私钥d
d = ( 20 + 1 ) / 3 d = (20+1)/3 d=(20+1)/3
6.A进行加密 m e / n m^e/n me/n 得到余数c
7.B解密的方式 c d / n c^d/n cd/n 得到余数m
安全性
B计算e和d,要传给A一个e,同时还要给A一个n
A要给B一个c
公开传播:n,e,c
解密需要:n,d,c
窃听者不知道d,不能进行解密
如果通过e求出d得先知道欧拉函数φ(n)
求欧拉函数φ(n)要求p和q, n = pq 进行质因数分解
分解小数字很简单,比如
21
=
3
∗
7
21=3*7
21=3∗7,但是分解一个1024位的数字就很困难
因为一个RSA,比较常用的是1024位二进制数n,目前人类还未做到
数学上做的一个结论,所以人们认为RSA算法比较保密
普通计算机算十年的大数质因数分解,量子计算机一个星期能算出来
所以每隔一段时间银行系统需要进行一次更新
简单运用
例:
p = 3 p =3 p=3, q = 11 q = 11 q=11对密文11,5,25进行加密
解:
n = p ∗ q = 33 n = p*q = 33 n=p∗q=33 φ ( n ) = ( p − 1 ) ∗ ( q − 1 ) = 20 \\varphi(n) = (p-1)*(q-1) =20 φ(n)=(p−1)∗(q−1)=20
公钥 e 取1到20之间一个整数,且与20互质,取e = 3
私钥 d = ( φ ( n ) + 1 ) / 3 = 7 d = (\\varphi(n)+1)/3 = 7 d=(φ(n)+1)/3=7
加密 1 1 e m o d n = 1 1 3 m o d 33 = 11 11^e\\ mod\\ n = 11^3\\ mod\\ 33 =11 11e mod n=113 mod 33=11
1 1 e m o d n = 5 3 m o d 33 = 26 11^e\\ mod\\ n = 5^3\\ mod\\ 33 =26 11e mod n=53 mod 33=26
1 1 e m o d n = 2 5 3 m o d 33 = 16 11^e\\ mod\\ n = 25^3\\ mod\\ 33 =16 11e mod n=253 mod 33=16
解密
c d m o d n = 1 1 7 m o d 33 = 11 c^d\\ mod\\ n=11^7\\ mod\\ 33=11 cd mod n=117 mod 33=11
c d m o d n = 2 6 7 m o d 33 = 11 c^d\\ mod\\ n=26^7\\ mod\\ 33=11 cd mod n=267 mod 33=11
c d m o d n = 1 6 7 m o d 33 = 11 c^d\\ mod\\ n=16^7\\ mod\\ 33=11 cd mod n=167 mod 33=11
以上是关于rsa加密算法简单介绍的主要内容,如果未能解决你的问题,请参考以下文章