基于二进制编码遗传优化的混合发电系统配置优化问题求解
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于二进制编码遗传优化的混合发电系统配置优化问题求解相关的知识,希望对你有一定的参考价值。
up目录
一、理论基础
遗传算法(Genetic Algorithm)是模拟自然界生物进化机制的一种算法即遵循适者生存、优胜劣汰的法则也就是寻优过程中有用的保留无用的则去除. 在科学和生产实践中表现为在所有可能的解决方法中找出最符合该问题所要求的条件的解决方法即找出一个最优解. 这种算法是1960年由Holland提出来的其最初的目的是研究自然系统的自适应行为并设计具有自适应功能的软件系统. 它的特点是对参数进行编码运算不需要有关体系的任何先验知识沿多种路线进行平行搜索不会落入局部较优的陷阱,能在许多局部较优中找到全局最优点是一种全局最优化方法[1-3]. 近年来,遗传算法已经在国际上许多领域得到了应用. 该文将从遗传算法的理论和技术两方面概述目前的研究现状描述遗传算法的主要特点、基本原理以及改进算法,介绍遗传算法的应用领域,并用MATLAB实现了遗传算法及最优解的求解.
科学研究、工程实际与国民经济发展中的众多问题可归结作“极大化效益、极小化代价”这类典型模型. 求解这类模型导致寻求某个目标函数(有解析表达式或无解析表达式)在特定区域上的最优解. 而为解决最优化问题目标函数和约束条件种类繁多,有的是线性的,有的是非线性的;有的是连续的,有的是离散的;有的是单峰值的,有的是多峰值的. 随着研究的深入,人们逐渐认识到:在很多复杂情况下要想完全精确地求出其最优解既不可能,也不现实,因而求出近似最优解或满意解是人们的主要着眼点之一. 总的来说,求最优解或近似最优解的方法有三种: 枚举法、启发式算法和搜索算法.
(1)枚举法. 枚举出可行解集合内的所有可行解以求出精确最优解. 对于连续函数,该方法要求先对其进行离散化处理,这样就有可能产生离散误差而永远达不到最优解. 另外,当枚举空间比较大时该方法的求解效率比较低,有时甚至在目前最先进的计算工具上都无法求解.
(2)启发式算法. 寻求一种能产生可行解的启发式规则以找到一个最优解或近似最优解. 该方法的求解效率虽然比较高,但对每一个需要求解的问题都必须找出其特有的启发式规则,这个启发式规则无通用性不适合于其它问题.
(3)搜索算法. 寻求一种搜索算法,该算法在可行解集合的一个子集内进行搜索操作以找到问题的最优解或近似最优解. 该方法虽然保证了一定能够得到问题的最优解,但若适当地利用一些启发知识就可在近似解的质量和求解效率上达到一种较好的平衡.
随着问题种类的不同以及问题规模的扩大,要寻求一种能以有限的代价来解决上述最优化问题的通用方法仍是一个难题. 而遗传算法却为我们解决这类问题提供了一个有效的途径和通用框架开创了一种新的全局优化搜索算法.
————————————————
遗传算法的主要步骤
首先,传统的遗传优化算法,其标准的优化过程如下所示:
步骤一:根据所需要处理的问题特点,选择问题解对应的编码,并给出一个初始群体,该初始群体包括N各染色体。
步骤二:计算遗传算法中群体的每一个染色体的适应函数值。
步骤三:当遗传算法的某一次迭代结果符合停止迭代条件,则算法停止迭代,如果不满足停止迭代条件,则以一个随机的概率分布值,从旧的种群中随机的选择N个染色体组成一个新的种群进行下一次的迭代。
步骤四:通过交叉得到N个染色体的交叉集合。
步骤五:设置一个较小的变异概率,使染色体中的某些基因进行变异,获得新的种群,并重复步骤二的计算过程。
其详细步骤如下: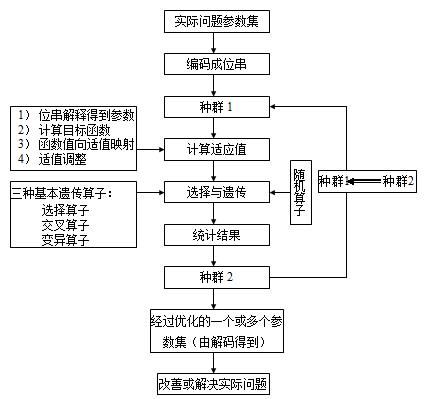
二、核心程序
%***************遗传算法二进制编码求解混合发电系统配置优化问题
function [Apv,Aw,Cp,CT,LPSP,Pdump,Pdeficit,SOC,Iteration,BestJ,Bfi]=GASolveHybirdSystemSize(WindDataPV,SolarDataPVR,LoadDataPV,Apv_max,Aw_max,Cb_max)
%**************遗传参数设置
Size=100;%种群大小
G=100;%迭代代数
CodeL=10;%编码长度
%**************问题解约束空间
u1max=Apv_max;
u1min=0;
u2max=Aw_max;
u2min=0;
u3max=Cb_max;
u3min=0;
%**************初始化编码
E=round(rand(Size,3*CodeL));
%**************GA主程序
for k=1:1:G
Iteration(k)=k;
for s=1:1:Size
m=E(s,:);
y1=0;y2=0;y3=0;
%*******************解码
m1=m(1:1:CodeL);
for i=1:1:CodeL
y1=y1+m1(i)*2^(i-1);
end
x1=(u1max-u1min)*y1/1023+u1min;
m2=m(CodeL+1:1:2*CodeL);
for i=1:1:CodeL
y2=y2+m2(i)*2^(i-1);
end
x2=(u2max-u2min)*y2/1023+u2min;
m3=m(2*CodeL+1:1:3*CodeL);
for i=1:1:CodeL
y3=y3+m3(i)*2^(i-1);
end
x3=(u3max-u3min)*y3/1023+u3min;
%******************适应度函数
[F(s),~,~,~,~,~]=GAFitnessFunction(x1,x2,x3,WindDataPV,SolarDataPVR,LoadDataPV);
end
Ji=1./F;
%*****************第一步:评估适应度
BestJ(k)=min(Ji);
fi=F; %适应度函数
[Oderfi,Indexfi]=sort(fi); %按照适应度大小从小到大排序
Bestfi=Oderfi(Size); %选取最佳适应度
BestS=E(Indexfi(Size),:); %最佳基因序列
Bfi(k)=Bestfi; %记录最佳适应度值
%*****************第二步:选择和复制操作
fi_sum=sum(fi);
fi_Size=(Oderfi/fi_sum)*Size;
fi_S=floor(fi_Size); %选择适应度较好的基因个体
kk=1;
for i=1:1:Size
for j=1:1:fi_S(i) %选择和复制操作
TempE(kk,:)=E(Indexfi(i),:);
kk=kk+1;
end
end
%*****************第三步:交叉操作
pc=0.60;%交叉概率
n=ceil(30*rand);
for i=1:2:(Size-1)
temp=rand;
if pc>temp %交叉条件
for j=n:1:30
TempE(i,j)=E(i+1,j);
TempE(i+1,j)=E(i,j);
end
end
end
TempE(Size,:)=BestS;
E=TempE;
%*****************第三步:变异操作
pm=0.1; %变异概率
for i=1:1:Size
for j=1:1:2*CodeL
temp=rand;
if pm>temp %变异条件
if TempE(i,j)==0
TempE(i,j)=1;
else
TempE(i,j)=0;
end
end
end
end
%保证第30个基因个体是最佳基因序列
TempE(Size,:)=BestS;
E=TempE;
end
%**********************解码最佳基因序列对应的各个参数优化值
y1=0;y2=0;y3=0;
m1=BestS(1:1:CodeL);
for i=1:1:CodeL
y1=y1+m1(i)*2^(i-1);
end
m2=BestS(CodeL+1:1:2*CodeL);
for i=1:1:CodeL
y2=y2+m2(i)*2^(i-1);
end
m3=BestS(2*CodeL+1:1:3*CodeL);
for i=1:1:CodeL
y3=y3+m3(i)*2^(i-1);
end
Apv=(u1max-u1min)*y1/1023+u1min
Aw=(u2max-u2min)*y2/1023+u2min;
Cp=(u3max-u3min)*y3/1023+u3min;
%**********************混合发电系统最佳配置的性能参数输出
[~,LPSP,Pdump,Pdeficit,SOC,CT]=GAFitnessFunction(x1,x2,x3,WindDataPV,SolarDataPVR,LoadDataPV);
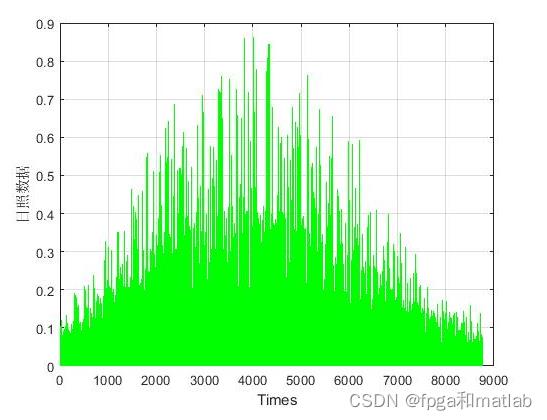
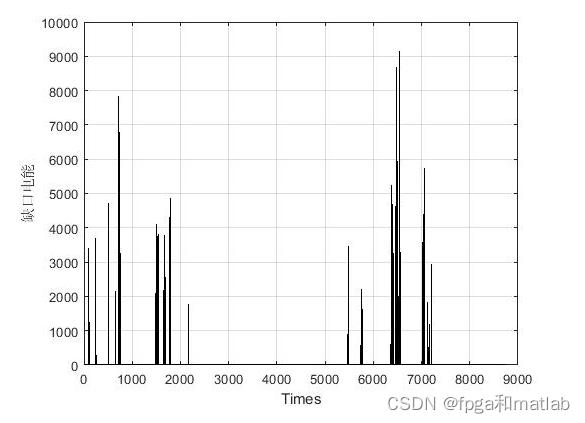
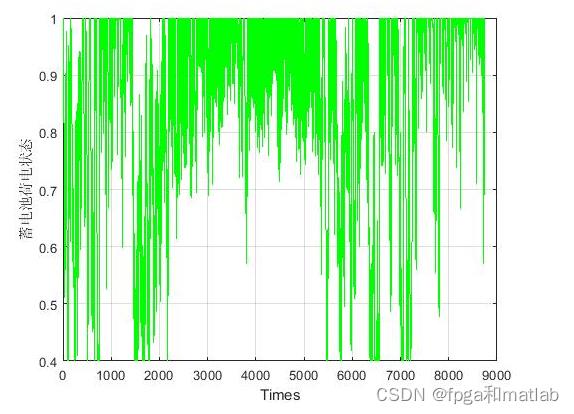
up103三、测试结果
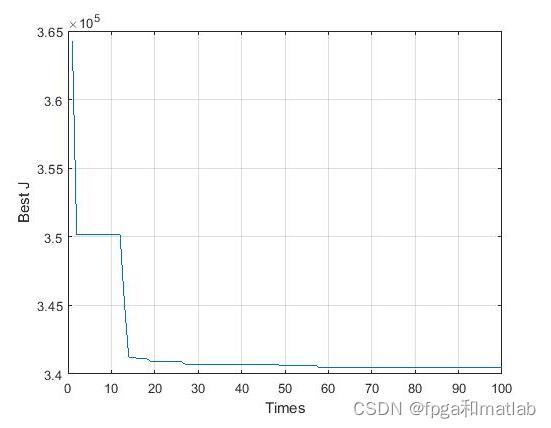
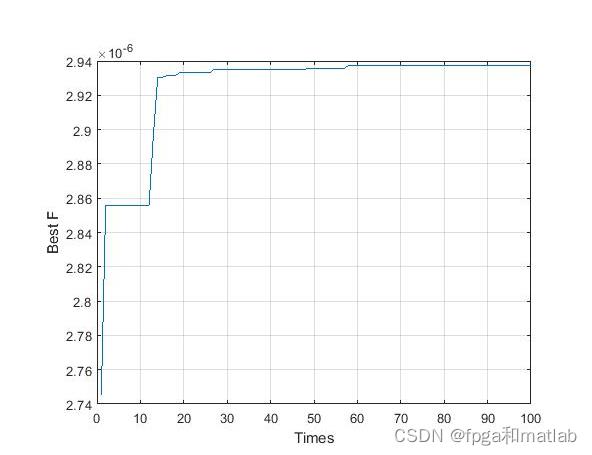
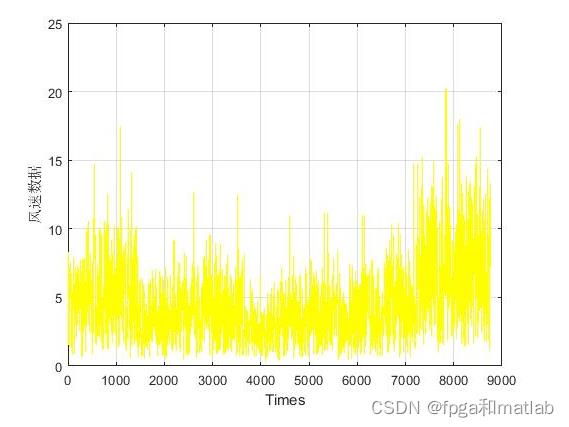
在matlab2021a中仿真得到如下的效果:


以上是关于基于二进制编码遗传优化的混合发电系统配置优化问题求解的主要内容,如果未能解决你的问题,请参考以下文章