模糊控制器设计源码程序
Posted fpga&matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模糊控制器设计源码程序相关的知识,希望对你有一定的参考价值。
clear % Clear all variables in memory
clc;
close all;
eold=0; % Intial condition used to calculate c
rold=0; % Intial condition used to calculate r
yeold=0; % Intial condition used to calculate yc
ymold=0; % Initial condition for the first order reference model
% Next, initialize parameters for the fuzzy controller
nume=11; % Number of input membership functions for the e
% universe of discourse
numc=11; % Number of input membership functions for the c
% universe of discourse
ge=1/2;,gc=1/2;,gu=5;
% Scaling gains for tuning membership functions for
% universes of discourse for e, c and u respectively
% These are tuned to improve the performance of the FMRLC
we=0.2*(1/ge);
% we is half the width of the triangular input membership
% function bases (note that if you change ge, the base width
% will correspondingly change so that we always end
% up with uniformly distributed input membership functions)
% Note that if you change nume you will need to adjust the
% "0.2" factor if you want membership functions that
% overlap in the same way.
wc=0.2*(1/gc);
% Similar to we but for the c universe of discourse
base=0.4*gu;
% Base width of output membership fuctions of the fuzzy
% controller
% Place centers of membership functions of the fuzzy controller:
% Centers of input membership functions for the e universe of
% discourse for of fuzzy controller (a vector of centers)
ce=[-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1]*(1/ge);
% Centers of input membership functions for the c universe of
% discourse for of fuzzy controller (a vector of centers)
cc=[-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1]*(1/gc);
gf=0;
fuzzyrules=[-1 -1 -1 -1 -1 -1 -0.8 -0.6 -0.4 -0.2 0;
-1 -1 -1 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2;
-1 -1 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4;
-1 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6;
-1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8;
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1;
-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1;
-0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1 1;
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1 1 1;
-0.2 0 0.2 0.4 0.6 0.8 1 1 1 1 1;
0 0.2 0.4 0.6 0.8 1 1 1 1 1 1]*gu*gf;
% Next, we define some parameters for the fuzzy inverse model
gye=1/2;,gyc=1/2;
% Scaling gains for the error and change in error for
% the inverse model
% These are tuned to improve the performance of the FMRLC
gp=0.2;
numye=11; % Number of input membership functions for the ye
% universe of discourse
numyc=11; % Number of input membership functions for the yc
% universe of discourse
wye=0.2*(1/gye); % Sets the width of the membership functions for
% ye from center to extremes
wyc=0.2*(1/gyc); % Sets the width of the membership functions for
% yc from center to extremes
invbase=0.4*gp; % Sets the base of the output membership functions
% for the inverse model
% Place centers of inverse model membership functions
% For error input for learning Mechanism
cye=[-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1]*(1/gye);
% For change in error input for learning mechanism
cyc=[-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1]*(1/gyc);
% The next matrix contains the rule-base matrix for the fuzzy
% inverse model. Notice that for simplicity we choose it to have
% the same structure as the rule-base for the fuzzy controller.
% While this will work for the control of the simple first order
% linear system for many nonlinear systems a different structure
% will be needed for the rule-base. Again, the entries are
% the centers of the output membership functions, but now for
% the fuzzy inverse model.
inverrules=[-1 -1 -1 -1 -1 -1 -0.8 -0.6 -0.4 -0.2 0;
-1 -1 -1 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2;
-1 -1 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4;
-1 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6;
-1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8;
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1;
-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1;
-0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1 1;
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1 1 1;
-0.2 0 0.2 0.4 0.6 0.8 1 1 1 1 1;
0 0.2 0.4 0.6 0.8 1 1 1 1 1 1]*gp;
% Next, we set up some parameters/variables for the
% knowledge-base modifier
d=1;
% This sets the number of steps the knowledge-base modifier looks
% back in time. For this program it must be an integer
% less than or equal to 10 (but this is easy to make larger)
% The next four vectors are used to store the information about
% which rules were on 1 step in the past, 2 steps in the past, ....,
% 10 steps in the past (so that picking 0<= d <= 10 can be used).
meme_int=[0 0 0 0 0 0 0 0 0 0];
% sets up the vector to store up to 10 values of e_int
meme_count=[0 0 0 0 0 0 0 0 0 0];
% sets up the vector to store up to 10 values of e_count
memc_int=[0 0 0 0 0 0 0 0 0 0];
% sets up the vector to store up to 10 values of c_int
memc_count=[0 0 0 0 0 0 0 0 0 0];
% sets up the vector to store up to 10 values of c_count
%
% Next, we intialize the simulation of the closed-loop system.
%
k_p=1; % The numerator of the plant. Change this value to study
% the ability of the FMRLC to control other plants. Also,
% you can make this a time-varying parameter.
zeta_p=.707;
% Damping ratio for the second order plant (could change this
% to see how the system will adapt to it)
w_p=1; % Undamped natural frequency for the plant (could change this
% to see how the system will adapt to it)
k_r=1;
% The numerator of the reference model. Change this value to study
% the ability of the FMRLC to meet other performance specifications.
a_r=1;
% The value of -a_r is the pole position for the reference model.
% Change this value to study the ability of the FMRLC to meet
% other performance specifications (e.g., a faster response).
t=0; % Reset time to zero
index=1; % This is time's index (not time, its index).
tstop=64; % Stopping time for the simulation (in seconds)
step=0.01; % Integration step size
x=[0;0]; % Intial condition on state of the plant
% Need a state space representation for the plant. Since our
% plant is linear we use the standard form of xdot=Ax+Bu, y=Cx+Du
% Matrix A of state space representation of plant
A=[0 1;
-w_p^2 -2*zeta_p*w_p];
B=[0; 1]; % Matrix B of state space representation of plant
C=[k_p 0]; % Matrix C of state space representation of plant
%
% Next, we start the simulation of the system. This is the main
% loop for the simulation of the FMRLC.
%
while t <= tstop
y(index)=C*x; % Output of the plant
% Next, we define the reference input r as a sine wave
r(index)=sin(.6*t);
ym(index)=(1/(2+a_r*step))*((2-a_r*step)*ymold+...
k_r*step*(r(index)+rold));
ymold=ym(index);
rold=r(index);
% This saves the past value of the ym (r) so that we can use it
% the next time around the loop
% Now that we have simulated the next step for the plant and reference
% model we will focus on the two fuzzy components.
% First, for the given fuzzy controller inputs we determine
% the extent at which the error membership functions
% of the fuzzy controller are on (this is the fuzzification part).
c_count=0;,e_count=0; % These are used to count the number of
% non-zero mf certainitie of e and c
e=r(index)-y(index);
% Calculates the error input for the fuzzy controller
c=(e-eold)/step;
% Calculates the change in error input for the fuzzy controller
eold=e;
% Saves the past value of e for use in the next time through the
% loop
% The following if-then structure fills the vector mfe
% with the certainty of each membership fucntion of e for the
% current input e
if e<=ce(1) % Takes care of saturation of the left-most
% membership function
mfe=[1 0 0 0 0 0 0 0 0 0 0]; % i.e., the only one on is the
%left-most one
e_count=e_count+1;,e_int=1; % One mf on, it is the
%left-most one.
elseif e>=ce(nume) % Takes care ofsaturation
%of the right-most mf
mfe=[0 0 0 0 0 0 0 0 0 0 1];
e_count=e_count+1;,e_int=nume; % One mf on, it is the
%right-most one
else % In this case the input is on the middle part of the
% universe of discourse for e
% Next, we are going to cycle through the mfs to
% find all that are on
for i=1:nume
if e<=ce(i)
mfe(i)=max([0 1+(e-ce(i))/we]);
% In this case the input isto the
% left of the center ce(i)and we compute
% the value of the mfcentered at ce(i)
% for this input e
if mfe(i)~=0
% If the certainty is not equal to zerothen say
% that have one mf on by incrementing our count
e_count=e_count+1;
e_int=i; % This term holds the index last entry
% with a non-zero term
end
else
mfe(i)=max([0,1+(ce(i)-e)/we]);
% In thiscase the input is to the
% right ofthe center ce(i)
if mfe(i)~=0
e_count=e_count+1;
e_int=i; % This term holds the index of the
% last entry with a non-zero term
end
end
end
end
% Next we will save the number of mfs that are on and the pointer
% e_int as to which rules were on. This vector of length
% 10 saves the last 10 values of e_count and e_int as time
% progresses (hence, it is a moving window).
% These will be used by the FMRLC knowledge-base modifier.
meme_count=[e_count meme_count(1:9)];
meme_int=[e_int meme_int(1:9)];
% The following if-then structure fills the vector mfc with the
% certainty of each membership fucntion of c for the current
% value of c (to understand this part of the code see the above
% similar code for computing mfe)
if c<=cc(1) % Takes care of saturation of left-most mf
mfc=[1 0 0 0 0 0 0 0 0 0 0];
c_count=c_count+1;
c_int=1;
elseif c>=cc(numc)
% Takes care of saturation of the right-most mf
mfc=[0 0 0 0 0 0 0 0 0 0 1];
c_count=c_count+1;
c_int=numc;
else
for i=1:numc
if c<=cc(i)
mfc(i)=max([0,1+(c-cc(i))/wc]);
if mfc(i)~=0
c_count=c_count+1;
c_int=i; % This term holds last entry
% with a non-zero term
end
else
mfc(i)=max([0,1+(cc(i)-c)/wc]);
if mfc(i)~=0
c_count=c_count+1;
c_int=i; % This term holds last entry
% with a non-zero term
end
end
end
end
% Next we will save the number of mfs that are on and the pointer
% c_int as to which rules were on. This vector of length 10
% saves the last 10 values of c_count and e_int as time progresses
% (hence, it is a moving window). These will be used by the FMRLC
% knowledge-base modifier.
memc_count=[c_count memc_count(1:9)];
memc_int=[c_int memc_int(1:9)];
% These for loops calculate the crisp output using only the non-
% zero premise of error,e, and change in error,c. This cuts down
% computation time since we will only compute
% the contribution from the rules that are on (i.e., a maximum of
% four rules for our case). Minimum is used for the premise
% and implication.
num=0;
den=0;
for k=(e_int-e_count+1):e_int
% Scan over e indices ofmfs that are on
for l=(c_int-c_count+1):c_int
% Scan over c indices ofmfs that are on
prem=min([mfe(k) mfc(l)]);
% Value of premisemembership function
% This next calculation of num adds up the numerator for the
% defuzzification formula. fuzzyrules(k,l) is the output center
% for the rule.base*(prem-(prem)^2/2 is the area of a symmetric
% triangle with base width "base" and that is chopped off at
% a height of prem (since we use minimum to represent the
% implication). Computation of den is similar but without
% fuzzyrules(k,l).
num=num+fuzzyrules(k,l)*base*(prem-(prem)^2/2);
den=den+base*(prem-(prem)^2/2);
end
end
u(index)=num/den;
% Crisp output of fuzzy controller that is the input
% to the plant
% Next, we perform computations for the fuzzy inverse model.
ye=ym(index)-y(index); % Calculates ye
yc=(ye-yeold)/step; % Calculates yc
yeold=ye; % Saves the value of ye for use the
% next time
ye_count=0;,yc_count=0; % Counts the non-zero certainties
% of ye and ycsimilar to how we did
% for the fuzzycontroller
% The following if-then structure fills the vector mfye with the
% certainty of each membership fucntion of ye (similar to the
% fuzzy controller). Notice that we use the same number of
% input membership functions as in the fuzzy controller -
% just for convenience - it does not have to be this way
if ye<=cye(1) % Takes care of saturation
mfye=[1 0 0 0 0 0 0 0 0 0 0];
ye_count=ye_count+1;,ye_int=1;
elseif ye>=cye(numye) % Takes care of saturation
mfye=[0 0 0 0 0 0 0 0 0 0 1];
ye_count=ye_count+1;,ye_int=numye;
else
for i=1:numye
if ye<=cye(i)
mfye(i)=max([0 1+(ye-cye(i))/wye]);
if mfye(i)~=0
ye_count=ye_count+1;
ye_int=i; % This term holds last entry with
% a non-zero term
end
else
mfye(i)=max([0,1+(cye(i)-ye)/wye]);
if mfye(i)~=0
ye_count=ye_count+1;
ye_int=i; % This term holds last entry with
% a non-zero term
end
end
end
end
% The following if-then structure fills the vector mfyc with the
% certainty of each membership fucntion of yc
if yc<=cyc(1)
mfyc=[1 0 0 0 0 0 0 0 0 0 0];
yc_count=yc_count+1;,yc_int=1;
elseif yc>=cyc(numyc)
mfyc=[0 0 0 0 0 0 0 0 0 0 1];
yc_count=yc_count+1;,yc_int=numyc;
else
for i=1:numyc
if yc<=cyc(i)
mfyc(i)=max([0 1+(yc-cyc(i))/wyc]);
if mfyc(i)~=0
yc_count=yc_count+1;
yc_int=i;
end
else
mfyc(i)=max([0,1+(cyc(i)-yc)/wyc]);
if mfyc(i)~=0
yc_count=yc_count+1;
yc_int=i;
end
end
end
end
% These for loops calculate the crisp output of the inverse model
% using only the non-zero premise of error,ye, and change in
% error,yc. This cuts down computation time (similar to the
% fuzzy controller). Minimum is used for the premise and the
% implication. To understand this part of the code see the
% similar code for the fuzzy controller.
invnum=0;
invden=0;
for k=(ye_int-ye_count+1):ye_int
for l=(yc_int-yc_count+1):yc_int
prem=min([mfye(k) mfyc(l)]);
invnum=invnum+inverrules(k,l)*invbase*(prem-(prem)^2/2);
invden=invden+invbase*(prem-(prem)^2/2);
end
end
% Next we compute the output of the fuzzy inverse model.
% If you want to let gp=0 to test the fuzzy controller by itself
% then you will have invden=0 and you will not be able to compute p.
% To make it possible to let gp=0 we put in the following
% if-then rule.
if gp==0
p=0;
else
p=invnum/invden; % Crisp output of inverse model
if abs(p)<.05, p=0; end % robustification term
end
% Next we modify the centers of ouput membership functions
% associated with the rules that were on d steps ago
% The indexing sheme is similar to the one used in the
% computation of the outputs of the fuzzy controller and
% fuzzy inverse model.
for k=(meme_int(d)-meme_count(d)+1):meme_int(d)
for l=(memc_int(d)-memc_count(d)+1):memc_int(d)
fuzzyrules(k,l)=fuzzyrules(k,l)+p;
end
end
% Next, the Runge-Kutta equations to find the next state.
time(index)=t;
F=A*x+B*u(index);
k1=step*F;
xnew=x+k1/2;
F=A*xnew+B*u(index);
k2=step*F;
xnew=x+k2/2;
F=A*xnew+B*u(index);
k3=step*F;
xnew=x+k3;
F=A*xnew+B*u(index);
k4=step*F;
x=x+(1/6)*(k1+2*k2+2*k3+k4); % Calculated next state
t=t+step; % Increments time
index=index+1; % Increments the indexing term so that
% index=1 corresponds to time t=0.
end % This end statement goes with the first "while" statement
% in the program
%
% Next, we provide plots of the input and output of the plant
% and the output of the reference model
%
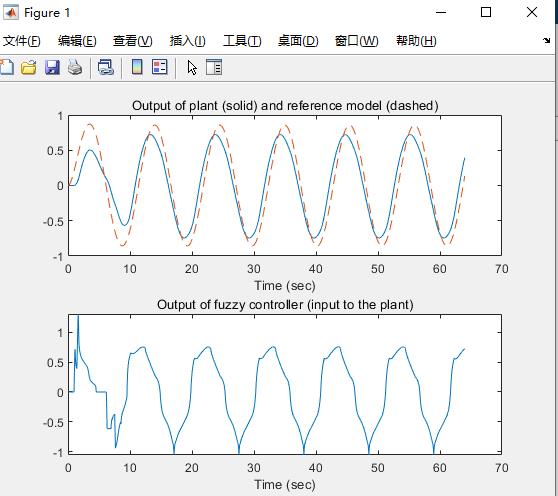
subplot(211)
plot(time,y,'-',time,ym,'--')
xlabel('Time (sec)')
title('Output of plant (solid) and reference model (dashed)')
subplot(212)
plot(time,u)
xlabel('Time (sec)')
title('Output of fuzzy controller (input to the plant)')
B170
以上是关于模糊控制器设计源码程序的主要内容,如果未能解决你的问题,请参考以下文章