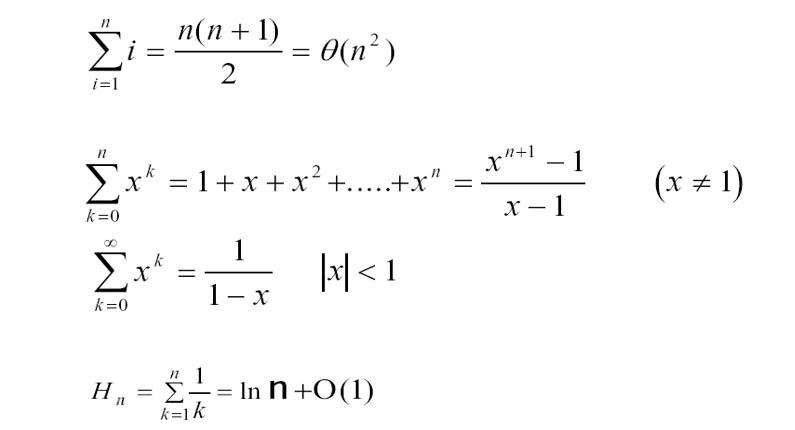学习算法不得不会的数学知识（突破学习算法的瓶颈）
Posted 卖寂寞的小男孩
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了学习算法不得不会的数学知识（突破学习算法的瓶颈）相关的知识，希望对你有一定的参考价值。
声明：本篇文章花费作者大量时间精力，所以是不可以转载的哦，以下内容有些概念较为烧脑，可能引起不适，请在奥特曼陪同下阅读（QAQ）。。。
目录
零.前言
这是算法设计与分析的第二讲，我们知道算法的设计是与数学分不开的，一个人的算法水平的下限是对模型掌握的多少，上限就是他的数学水平（我们算法大佬说的），那么就有人说了，我的数学水平也不高啊，怎么学好算法？数学水平不高有问题吗？没有问题。看了这篇文章，搞定算法分析的数学基础。
1.计算复杂性函数的阶
1.增长的阶
1.增长率
描述算法效率的方法：增长率
而我们引入阶的概念，就是为了研究算法的增长率，注意不是描述执行的时间。因为一个算法执行的时间不仅与算法本身有关，还和其他因素有关（比如硬件性能和使用的语言等），我们希望只根据算法本身来描述算法的好坏，因此没有选择时间作为参考。但其实描述算法运行效率的指标，就是抛弃其他所有因素算法所运行的时间，只不过这个时间没有办法准确计算，所以用时间的增长率代替。
所谓增长率，就是随着输入指标n的逐渐增大，运行时间的增长率，而非运行时间本身。
而程序运行的纯时间（不考虑其他因素），与代码的语句执行次数成正比，下图()内的内容表示的就是一个程序的大概执行语句数。所以可以用含有n的表达式代表算法的执行效率（可以看看数据结构部分）。而增大输入规模后纯运行时间的增长率就等价于执行代码数的增长率。不知道你听懂了没有呀。
增长率即为当多加入一组数所需要增加的大致时间或者增加的代码大致执行条数。还要注意一下，这里的增长率只的是广义的增长率，不能严格的按照数学方式来计算增长率，如果很细地计算的话几乎没有一段代码的准确增长率是相同的。为什么可以这么做呢？因为一点点的不同对运算的纯时间影响并不大，所以可以将它们归于一类复杂度。
2.常见的阶
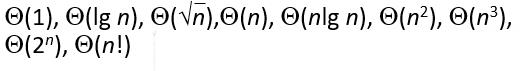
我们来看这一段θ()阶，会发现
1.从左到右算法的复杂度越来越高，即与()中复杂度为同阶的算法的运行效率越来越低。
2.所有阶的复杂度都是初等函数的集合。
每一个()里的内容表示按算法复杂度分出来的一类函数，θ()表示这一类函数的集合。
当你把一个本应该是n^2的算法复杂度搞成nlgn的时候，你就是一个超级大佬了（我们老师说的）。
2.增长函数
1.增长函数的性质
1.输入规模大。
2.不考虑低阶项和常系数。
3.只考虑高阶项
增长的记号：Θ，O，Ω，o，ω
2.Θ阶（同阶函数集合）
所谓Θ()，就是与()内表达式运算时间增长率相同的表达式的结合，一个表达式代表一个程序的时间复杂度。
1.定义：
Θ(g(n))={f(n)|存在c1,c2>0,n0,当任意n>n0时，c1g(n)>f(n)>c2g(n)}。成为与g(n)同阶的函数集合，即满足条件的所有f(n)都与g(n)同阶。
用图像来表示一下：
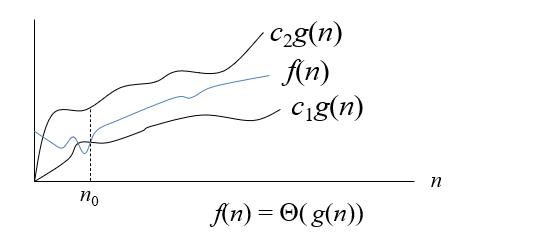
2.解释
这里表示的是f(n)与g(n)，Θ阶所描述的就是同阶函数。n0之前的内容不需要看，因为输入数据过小是没有办法分析时间复杂度的。
显然c1g(n)和c2g(n)的增长率是相同的，因为计算时间复杂度的时候是去掉常数的，所以c1g(n)与c2g(n)都是g(n)类型的，既然属于同一个类型，那么增长率（注意是广义的增长率）一定相同。
由于f(n)始终在两个增长率相同的函数中间，所以f(n)的增长率与这两个函数相同，即f(n)也属于g(n)的类型，所以f(n)与g(n)是同阶的。
3.例题
1.证明：(1/2)n^2-3n=θ(n^2)
即证存在c1和c2，n0>0，当n>n0时对任意n使得c1n^2<(1/2)n^2-3n<c2n^2
所以c1<1/2-3/n<c2，存在n0=7，即n>7时，存在c2=1/2，c1=1/14使得原式成立，所以得证。
2.证明：6n^3!=θ(n^2)
若存在c1和c2，n0>0，当n>n0时对任意n，使得c1n^2<6n^3<c2n^2。
所以c1<6n<c2.当n>c2/6时，与6n<c2矛盾，所以得证。
3.大O阶（低阶函数集合）
1.定义：
O(g(n))={f(n)|存在正常数c和n0满足对于所有n>=n0，0<=f(n)<=cg(n)}，记作：f(n)属于O(g(n))，或者f(n)=O(g(n))。
用图像表示为：
我们引入其他阶的目的在于，有一些程序的复杂度无法直接计算得到但是可以获得其复杂度的取值范围。
2.解释
显然，当n>n0时f(n)一直在cg(n)的下方，而cg(n)与g(n)是同阶的（即增长率是广义相同的），所以随着n的增大代码执行量的增长率f(n)是<=g(n)的，即时间的增长率是小于等于g(n)，所以f(n)的效率低于g(n)，O(g(n))代表的是所有复杂度小于等于g(n)的函数的集合。
3.Θ阶与O阶的关系
1.f(n)=θ(g(n))，则f(n)=O(g(n))。
因为f(n)与g(n)同阶复杂度相同，O(g(n))包含所有复杂度小于等于g(n)的函数，f(n)是属于O(g(n))的。
2.Θ标记强于O标记
因为Θ阶计算的是同阶，而O阶计算的是最高阶，好比做一份工作，Θ阶表示明确地知道一小时可以做完，但O阶只知道十小时内可以做完，所以Θ阶是优于O阶的。
3.Θ(g(n))属于O(g(n))
对于同一个g(n)O阶的范围比θ阶大。
4.an+b=O(n^2)
因为an+b的算法复杂度是Θ(n)类型的，O(n^2)包含所有比n^2复杂度低的函数，所以对于an+b这样算法复杂度是n的算法是被O(n^2)包含在内的。同理n=O(n^2)。
5.O(n)=O(n^2)但是O(n^2)!=O(n)
前面讲过了等号是包含的意思，是后者包含前者，不能调换顺序。
6.O标记表示渐进上界，Θ标记表示渐进紧界。
7.Θ阶表示的是基本运算时间，但O阶表示的是最坏的结果即最长运行时间。
4.Ω阶（高阶函数集合）
1.定义
Ω(g(n))={f(n)|存在正常数c和n0，对于所有n>=n0，0<=cg(n)<f(n)}记作f(n)∈Ω(g(n))或者f(n)=Ω(g(n))。
用图像来表示是这样的：
2.解释
对比大O阶，Ω(g(n))表示的是所有比g(n)低阶的函数的集合。
3.θ阶，大O阶，Ω阶的关系
1.对于f(n)和g(n)，f(n)=Θ(g(n))，当且仅当f(n)=O(g(n))，f(n)=Ω(g(n))。
f(n)比g(n)阶高，同时比g(n)阶低，所以g(n)与f(n)是同阶的，反之也成立。
2.O表示渐进上界，Θ表示渐进紧界，Ω表示渐进下界。
3.Ω用来描述的是运行时间最好的情况。
对于插入排序，它的算法复杂度既属于O(n^2)又属于Ω(n)。
5.小o阶（严格低阶函数集合）
1.定义：
o(g(n))={f(n)|对于任意正常数c，存在一个整数n0，从而对所有n>=n0，满足0<=f(n)<cg(n)}。记作f(n)∈o(g(n))，或者f(n)=o(g(n))。
用图像来表示是这样的：
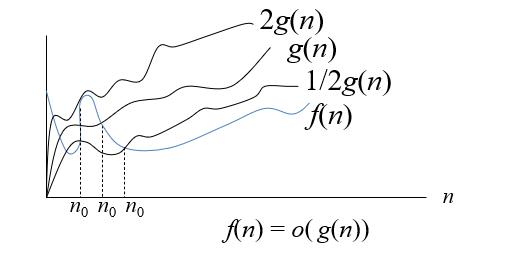
2.解释
我们发现这个定义和大O阶的定义很相似，只不过将存在一个c改成了任意c（注意对于每一个c都有一个n0与之对应），o(g(n))代表的意思是所有复杂度小于g(n)的函数的集合，而O(g(n))表示的是所有复杂度小于等于g(n)的集合，两者只差了一个等号。
在大O阶中，存在一个c使得cg(n)>f(n)，这个时候f(n)的增长率可以小于cg(n)（即g(n)的增长率）这样f(n)就永远小于g(n)了，但f(n)的增长率也可以等于（广义上的）cg(n)，这种情况下两者基本是平行的，f(n)依然一直小于cg(n)（同时也是g(n)）。因为c本身是固定的。
在小o阶中，对于任意c都有cg(n)>f(n)，当f(n)的增长率小于cg(n)时（g(n)），f(n)将永远小于g(n)，当f(n)的增长率等于g(n)时，那么对于一个很小的c来说，f(n)就有机会大于cg(n)（g(n)）,这就是两者的区别。
总结一下，
大O(g(n))包含的函数：f(n)的增长率（复杂度）<=g(n)。
小o(g(n))包含的函数：f(n)的增长率（复杂的<g(n）。
3.例题
1.证明：2n=o(n^2)
对于任意c>0,存在一个n0当n>n0时，使得2n<c(n^2)
即2<cn，即2/c<n
对于任意的c总存在一个n0=2/c使得不等式成立，所以得证。
2.证明：2(n^2)!=o(n^2)
若成立则，对于任意的c，存在一个n0，当n>n0时，使得2(n^2)<c(n^2)
即2<c，当c=1时不成立，与对任意c都成立矛盾，所以得证。
6.小ω阶（严格高阶函数）
1.定义：
ω(g(n))={f(n)|对于任意正常数c，存在一个整数n0，从而对所有n>=n0，满足0<=f(n)<cg(n)}。记作f(n)∈ω(g(n))，或者f(n)=ω(g(n))。
2.解释
与小o阶是一样的，表示的是不紧的下界，大Ω(g(n))表示的是所有阶数大于等于g(n)的函数的集合，小ω阶表示所有阶数大于g(n)的集合。即n^2=Ω（n^2）但是n^2!=ω(n^2)。
7.渐进符号的性质
1.传递性
传递性对于五个阶来说都是通用的
比如f(n)=Θ(g(n))，且g(n)=Θ(h(n))，则f(n)=Θ(h(n))。
2.自反性
对于Θ，O，Ω阶有自反性。f(n)=Θ(f(n))。
3.对称性
只对Θ阶，f(n)=Θ(g(n))，则g(n)=Θ(f(n))。
4.反对称性
f(n)=O(g(n))，当且仅当g(n)=Ω(f(n))。
f(n)=o(g(n))，当且仅当g(n)=ω(f(n))。
2.和式的估计与运算
1.为什么要进行和式的估计与运算
和式的估计与运算在我们计算一段代码的复杂度中经常用到，我们之前所谓的f(n)，g(n)函数的集合都是一段代码的执行步骤的和，然后才能进行一些大O阶什么之类的运算。说白了就是要先计算程序一共执行了多少段代码，再对结果进行分类。因此掌握计算和式的方法是非常必要的，以下内容均为计算和式（算法的复杂度）的常用数学方法。
2.和式的估计
1.线性和
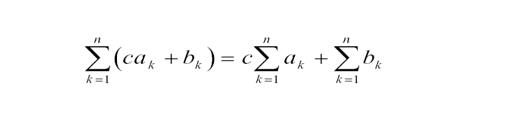
这是最基本的数学公式，看来算法和高数的关系也是相当巨大呀。。博主就直接放图片了，这个求和符号太难打了。。
2.级数
提一下最后一个，叫调和级数，高数里总考判断题的那个级数就是这个东西。
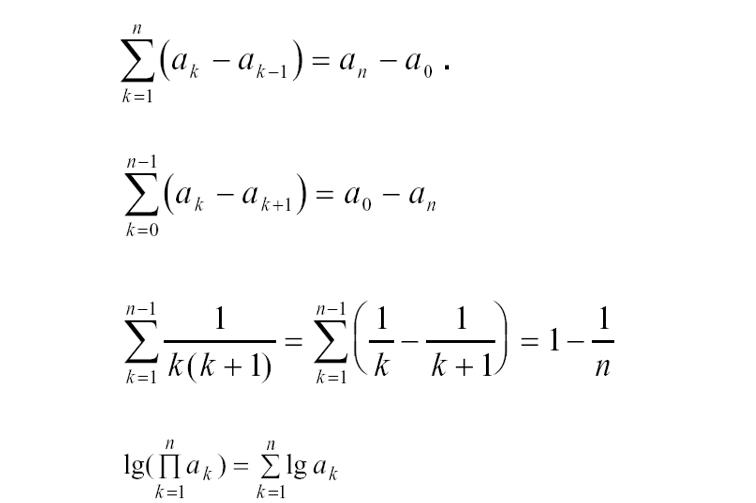
这几个就是高中时算的最6的那几个，裂项相消啊，总之前后消去，剩下首尾。
3.和的界限
例题一：
还是贴图片吧，这个Σ的上下内容没法打，看着也比较费劲，能把人绕晕。。
我们来分析一下这道题：即直接根据定义往里套就行，存在一个c，n0使当n>n0的时候，左式小于等于c3^n即可，证明过程如下：
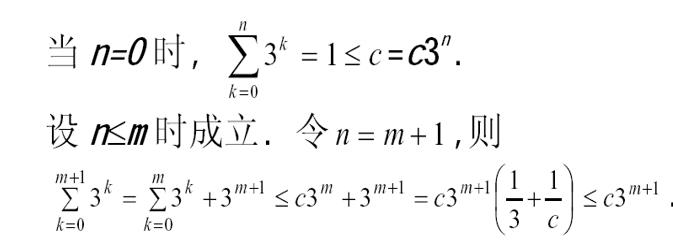
这段证明运用到了数学归纳法，即先确定首元素满足，然后再证明在前一个元素满足的条件之下，后一个元素也满足，则所有元素就都满足了，这其实没有证明完毕，当最后的式子成立才满足条件，即存在一个c使最后一步的式子成立我们可以发现当c>=3/2时都成立，所以得证。
例题二：
这是一段错误证明的式子，看了这个ppt是不是很懵。常数c?什么常数c，只有视力不好的人才能看到常数c，像我这样的国家代码之才，还常数c?其实做这样的题目的时候一定要拆开了来看，特别要注意=O(n)中的等号不是等号，是赋值符号，注意下面的式子第二个等号代表的意思是，存在一个常数c1使得Σk+(n+1)<=c1n+(n+1)，这段是没问题的，问题出现在下一个等号上，如果下一个等号成立，意味着存在常数c2，使得c1n+(n+1)<=c2n，即(c1+1-c2)n<=-1恒成立，由于c1,c2都是常数，值未知，所以不能保证随着n的增大不等式始终成立。也可以这样理解，因为c1和c2的大小未知，所以不能确定c1n+(n+1)<=c2n恒成立。
4.直接求和的界限
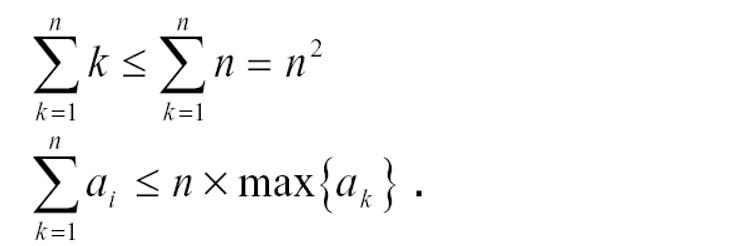
这两个式子很重要，大家一定要记牢啊！
例题1：
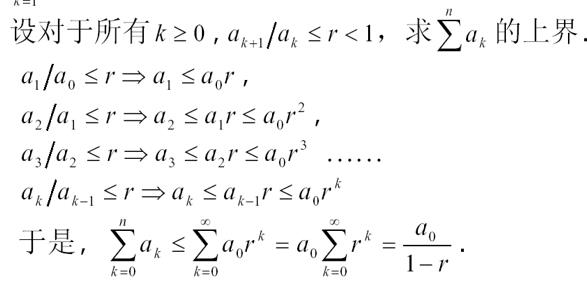这种题代表一类题型，也是我们高中经常要看的一种消去法，（用算法大佬的话来讲，他的每一道题都不可能白出）。这道题是将每一个式子都列出之后再相除进行消去，只剩下了首项和尾项，即得到的结果是ak/a0<=r^k，然后两边再分别套积分号来计算，最终得到结果，其中最后计算r的积分的式子应用到了前面的内容。这种题的解题思路就是先找到与ak等价的式子，根据题中的不等式找关系，然后再套积分号，最终根据常数的计算公式来进行求解。
例题2：
和上一题是同一个类型，首先找出与积分式等价的式子，设每一个通项是bk，只需用b(k+1)/bk得到这个值<=2/3，然后将k=1,2,3,4,,,依次带入相除，找到b(无穷）/b1的值，经过博主与舍友的讨论认为这个答案有凑数的嫌疑，不算准确的答案，最后一个表达式中的k应该改为k-1，即(1/3)*(2/3)^(k-1)，那样的话上界就不是一了，但是对于程序来说其实都是大O(1)所以问题不大。
例题3：
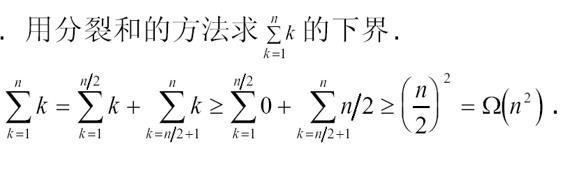
这里采用了放缩的方法，放了一半的元素，注意这不是数学题，不需要那么精确地计算出结果，只要算出来阶数即可，利用上面的那两个表达式就可以证明出下界是Ω(n^2)。
例题4：
同样的套路，先用a(k+1)/ak得到一个表达式，寻找从哪一项开始这个表达式是小于1的（因为我们已经猜测表达式的上界是O(1）)，然后将它们拆开，前一项是一个常数，不用管，后一项的值始终小于1，因此它的上界是O(1)。
例题5：
这题是所有题中最让我懵逼的一道，没点数学基础真不敢出来混。观察这组数据，每一个括号中第一个数是2的倍数，每个括号含有的项数也是二的倍数，这两个二的倍数是相等的。这里的i代表有多少组数据，设有m组数据则1+2^1+2^2+....2^(m-1)=n所以解出m=log(2)(n+1)，下面是2，上面是（n+1），所以第一个不等式成立（吐槽一下这题老师是念ppt讲的，连log下面的2没了都没发现），前一个Σ符号表示的是有几组数，后面的Σ符号表示的是每一组数加起来，1/(2^i+j)表示的是每一个数，这样你是不是就通透了呀。
例题6：
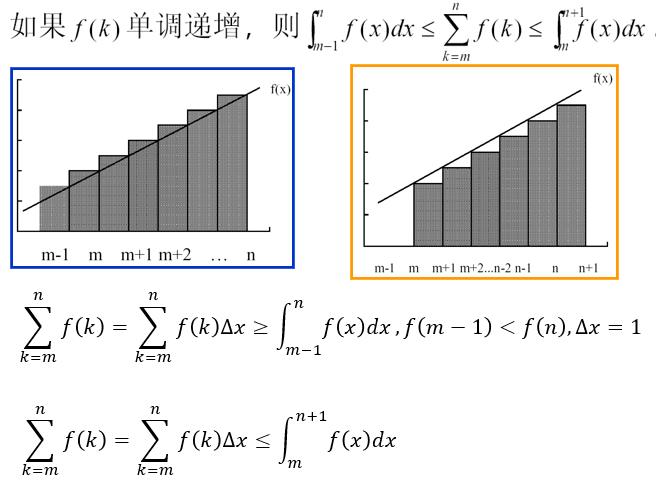证明上述式子，先看前一个不等号，前面的式子表示的是一个积分，是连续的，后一个表示的是散点相加，我们知道积分的值表示的是函数图像与x轴围成的面积，我们对散点相加的乘以1，那么它也会表示一个面积，如第一个图所示，除去相同部分我们发现前一个积分面积剩下m-1到m-2这个梯形的面积，后面的散点图表达式剩下的是(n-m)个小三角，由于n是趋近于无穷大的，所以小三角的面积和一定大于(m-1)到(m-2)这个梯形的大小。当n是常数时无法判断。
第二个图我认为画的有点问题，我们还是按照第一个图来理解，当除去相同的部分之后，散点图剩下(n-m)个小三角，积分图剩下最后一个梯形，将小三角往梯形里填充，很明显发现它们的面积和是小于梯形面积的（注意我们目前研究的是递增函数），当n时常数的时候也是如此。
既然递增函数的结果是这个，那么递减函数的结果就是将它们反过来，即：
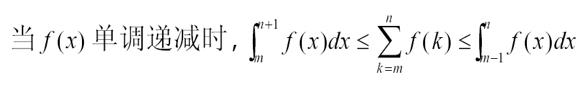
例题7：
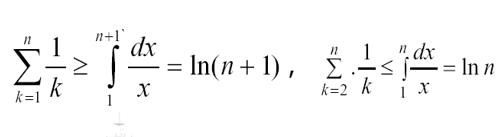
两个结论，经常用到，记住就会，记不住就不会。
3.递归方程
1.递归的定义
递归定义是数理逻辑和计算机科学用到的一种定义方式，使用被定义对象的自身来为其下定义（简单说就是自我复制的定义）。递归定义(recursive definition)亦称归纳定义，一种实质定义，指用递归的方法给一个概念下的定义。
2.递归方程的形式
T(n)=T(n/a)+bn+..
即有两个T()的函数项，递归方程研究了T(n)与T(<n)的函数关系。
3.递归方程的初始条件
递归方程需要有基本情况或者初始条件。
比如假设T(n)=T(n/2)+11n最后计算出T(n)=1
与T(n)=T(n/2)+11n计算出T(n)=10000这两个式子虽然是不同的。
但是两者的T(1)=O(n)，因此我们可以忽略具体的值。
4.求解递归方程的三个主要方法
1.替换（代入）方法
步骤：（1）猜想
（2）数学归纳法证明
猜想的方法：
1.联想已知的T(n)
例题：求解T(n)=2T(n/2+17)+n
我们发现T(n)=2T(n/2+17)+n与T(n)=2T(n/2)+n只差了一个17，而后者的上界是O(nlgn)，随着n的增大，这个17所产生的影响越来越小，所以我们猜测原式的时间复杂度是O(nlgn)。
2.先证明不确定的上下界，然后缩小不确定性的范围
例题：求解T(n)=2(n/2+17)+n
首先证明比较容易的上下界，首先计算出T(n)=Ω(n)，然后计算出T(n)=O(n^2)，而nlgn的复杂度刚好在n和n^2之间，所以估计出其上限是O(nlgn)。
2.细微差别的处理
当我们的猜测是正确的时候，但是数学归纳法无法证明出来。
解决方法：从猜想中减去一个低阶项。
3.例题：
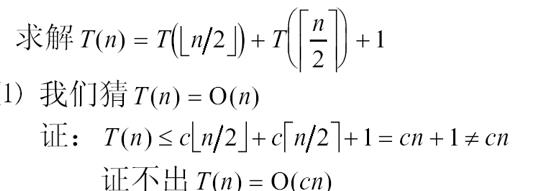
向上向下取整的符号了，我也不会打印，所以还是贴图片吧。。。。
ppt还是写的太简洁了，我把他详细地说一说，首先我先猜想T(n)=O(n)，即猜测存在一个c，对于任意的n，存在一个n0使得T(n)恒小于等于O(n)。即T(n/2)[向下取整]<=c(n/2)[向下取整]，T(n/2)[向上取整]<=c(n/2)[向上取整]。我们想证明猜想成立也就是要证明T(n)<=cn成立，但是这样只能证明出T(n)<=cn+1，所以证明的不对。
下面就需要应用到细微差别处理的方法：
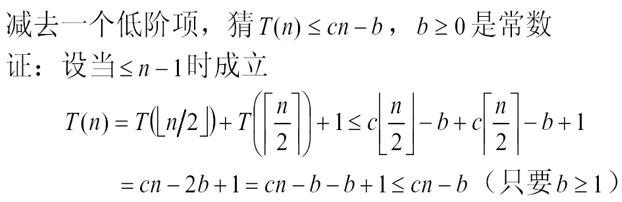
注意这里虽然减去了一个常数项，(cn-b)表示的依然是O(n)，如果假设T(n)=O(n)，此时假设的是存在一个c，对于任意的n存在一个n0使n>=n0的时候，T(n)<=cn-b<=cn，证明了T(n)<=cn-b也就证明了T(n)<=cn。要证明猜想成立就要证明T(n)<=cn。
我们观察式子，T(n)<=cn-2b+1，由于b是任取的整数，所以当b>=1时，T(n)<=cn-b<=cn，所以成立，T(n)=O(n)。
3.变量替换方法
顾名思义，通过变量替换，将递归方程变换为熟悉的方程。
例题：求解T(n)=T(√n)+lgn
令m=lg(n)，则n=10^(m)，√n=10^(m/2)，所以原式变成了T(10^(m))=T(10^(m/2))+m
令S(m)=T(10^m)所以原式为，S(m)=S(m/2)+m，所以S(m)=O(mlgm)，所以T(10^m)=O(mlgm)，因为10^m=n，所以T(n)=O(lgn*lg(lgn))。
2.迭代（递归树）方法
1.步骤
1.画出递归树。
2.循环地展开递归方程。
3.将递归方程转化为和式。
4.使用求和技术求解。
2.递归树求解
整个式子的时间复杂度就是将所有的节点加在一起，下面我们来分析一下，为什么会画出这样一棵树：
首先T(n)包含四个部分，前三个部分是T(n/4)[向下取整]，即树的分叉部分，最后一个部分是树根部分，即为Θ(n^2)部分，由于所有的树的分叉部分都代表了一棵树，所以其实最后加起来的部分只有树根部分，对于第一次递归来说，三个树杈部分又是一个树，即T(n/4[向下取整])=3T(n/16[向下取整])+Θ((n/4)^2[向下取整])。而后者等于Θ((n/4)^2)，因此它对应的树根节点就是c(n/4)^2，依次类推，知道最终节点变成了T(1)。这是因为原本n是一个很大的数，当走到T(1)时拆分之后的结果就变成了0，无法再分出树杈了。
因此整道题的求解过程是：
首先计算树的高度，n/4^(m-1)=1，解得m=log(4)(n)+1.
然后计算最后一行的元素个数：m=3^(log(4)(n)+1-1)=3^(log(4)(n))=n^(log(4)(3))。两边同时取log(4)，你就会解了。
这是整道题的过程，是不是数学很重要。。不看很难解出来。
3.例题
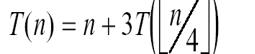
用我拙劣的迷之画风来画一下这棵树：
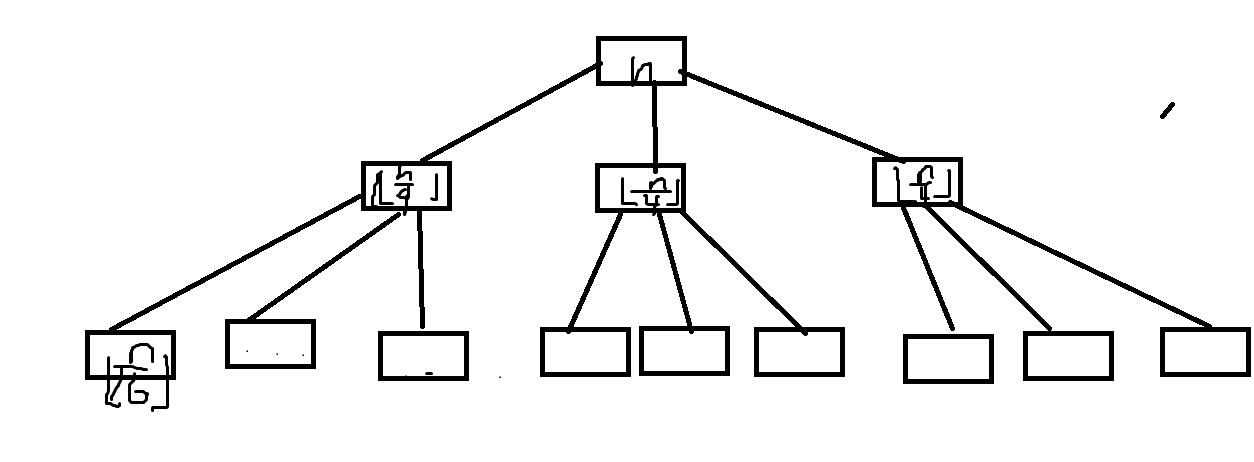
后面几个框里都是n/16向下取整，，画太丑了，不画了。。
注意这里的每个节点是带有向下取整的符号的，和上一题不同，上一题的常数项是 Θ(n^2)就算是向下取整后依然是c(n^2)，但是这里是n所以列出来的式子是：
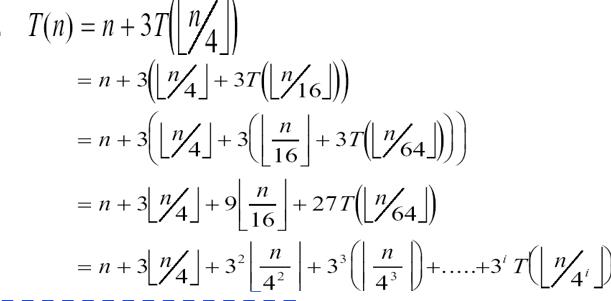
注意这里有两个他ppt写错了，是向下取整，不是绝对值。
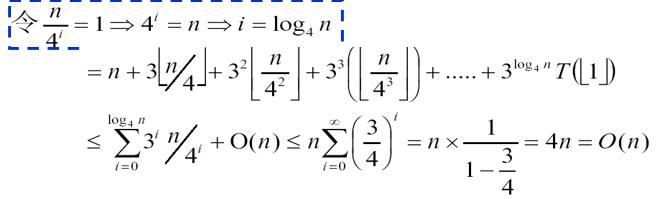所以最终上限是O(n)。
3.Master定理方法
1.适用类型
T(n)=aT(n/b)+f(n)。
其中a表示子问题数量，b表示子问题从原问题缩小的比例，f(n)表示将问题分解和子问题分解整合的代价。其实这些都不用管，记住上面的形式即可。
3.定理内容
前提：a>=1且b>1，T(n)定义在非负整数集合上。
1.当f(n)=O(n^(log(b)(a)-ε))时（ε>0是一个常数），即f(n)<=cn^(log(b)(a)-ε)时，T(n)=Θ(n^(log(b)(a))。
2.当f(n)=Θ(n^(log(b)(a))时，则T(n)=Θ(n^log(b)(a)lgn)。
3.当f(n)=Ω(n^(log(b)(a)+ε))时，ε>0是一个常数，且对于所有充分大的n，af(n/b)<=cf(n)，c<1是常数，则T(n)=Θ(f(n))。
注：下划线部分为正则条件，即必须满足的条件。
ε存在一个即可。
4.一张图记忆
这张图总结的到位，点个赞，注意最后一个式子的正则条件。还有第一个和第三个式子使用时的
ε别忘了。
5.例题
例题1：
T(n)=9T(n/3)+n
此时a=9，b=3，f(n)=n。
n^(log(b)(a))=n^2，存在ε使得f(n)=n=O(n^(2-ε))，
符合第1种情况，所以T(n)=Θ(n^2)。
例题2：
T(n)=T(2n/3)+1
此时a=1，b=3/2，f(n)=1.
n^(log(b)(a))=1，此时f(n)=Θ(n^(log(b)(a))，
符合第二种情况，所以T(n)=Θ(lgn)。
例题3：
T(n)=3T(n/4)+nlgn
此时a=3，b=4，f(n)=nlgn
n^(log(b)(a))=n^(log(4)(3))，存在ε使得f(n)=Ω(n^(log(4)(3)+ε))，这是因为nlgn的复杂度是大于n的，所以存在ε使之大于n^(log(4)(3)+ε。
此时还要证明正则条件af(n/b)<=cf(n)，c<1
即证(3n/4)lg(3n/4)<=cnlgn，化简一下，当c=3/4时，成立，注意c也是存在而不是任意。
所以T(n)=Θ(nlgn)。
例题4：
T(n)=2T(n/2)+nlgn
此时a=2，b=2，f(n)=nlgn
n^(log(b)(a))=n，不存在ε使得f(n)=Ω(n^(1+ε))，
所以Master定理不好使。
4.总结
经过两个星期的奋战，终于搞定了这篇博客，不得不说写这篇博客真的很烧脑，因为好多老师在课上一笔带过的知识点，博主基本上都给出了严格的证明（有的是和同学一起讨论的），吐个槽这ppt做的实在是太简便了。。。还有点错误，不过在博主的火眼金睛之下都给他找到了，并在博文中用红笔标注了出来，写完这篇博客我感觉自己的算法水平还是有所提高，如果你真的读完了呢，相信再碰到类似的问题也能够轻松求解吧（比心）。
如果可以的话，三连关注一下吧（卑微微）。如果你发现博文有错误，也欢迎私聊博主呀！
以上是关于学习算法不得不会的数学知识（突破学习算法的瓶颈）的主要内容，如果未能解决你的问题，请参考以下文章