OpenCV中的「透视变换 / 投影变换 / 单应性」—cv.warpPerspectivecv.findHomography

Posted 2021-10-04 虾米小馄饨

文章目录

• • 引言
  • 透视变换（projective transform）
  • 单应性（Homography）
  • opencv代码
  • • 仿射变换相关函数
    • 投影变换相关的函数
    • 鸟瞰图代码示例
  • 小结

引言

图像的几何变换通常包括拉伸、缩放、扭曲和旋转等操作。

对于平面区域来说，分为两类几何转换：¹

• ⭐️仿射变换（affine transform），基于2x3矩阵进行变换。指图像可以通过一系列的几何变换来实现平移、旋转等多种操作。该变换能够保持图像的平直性和平行性。平直性是指图像经过仿射变换后，直线仍然是直线；平行性是指图像在完成仿射变换后，平行线仍然是平行线。
• ⭐️透视变换（projective transform），基于3x3矩阵进行变换。透视变换将视锥体转换为长方体形状，视锥体的近端比远端小，具有扩大相机附近物体的效果。透视变换可以改变平行关系，将矩形映射为任意四边形。

透视变换通常被用于当作从特定角度观察三维平面的计算方法（非垂直观测），在三维视觉领域具有广泛的应用。

本文主要介绍opencv中的透视变换（projective transform）原理和代码。

透视变换（projective transform）

透视变换，又称为投影变换，是指将坐标为$(X,Y,Z)$的物理点$Q$映射到投影平面上坐标为$(x,y)$的点$q$的过程¹。

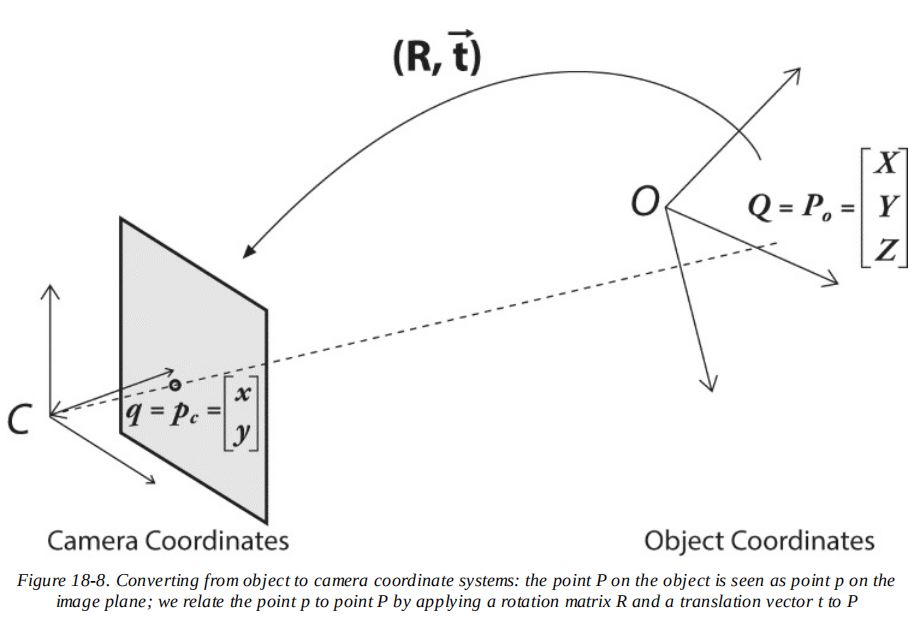
基本投影几何

将定义摄像机参数的矩阵（包含$f_x,f_y,c_x,c_y$）称为摄像机的内参数矩阵（camera intrinsics matrix）。

物理世界中的点$Q$投影到摄像机上的点$q$的过程，可以用下式表示：

$$q=M\cdot Q,其中q=\left[\begin{array}{c}x\\ y\\ w\end{array}\right],M=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]，Q=\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$

单应性（Homography）

计算机视觉中，平面的单应性被定义为从一个平面到另一个平面的投影映射。（注：“单应性”在不同学科有不同含义，在数学上有更通用的意思。这里仅说明计算机视觉中的单应性。¹）

二维平面上的点映射到摄像机成像画面上的映射，就是平面单应性的典型例子。

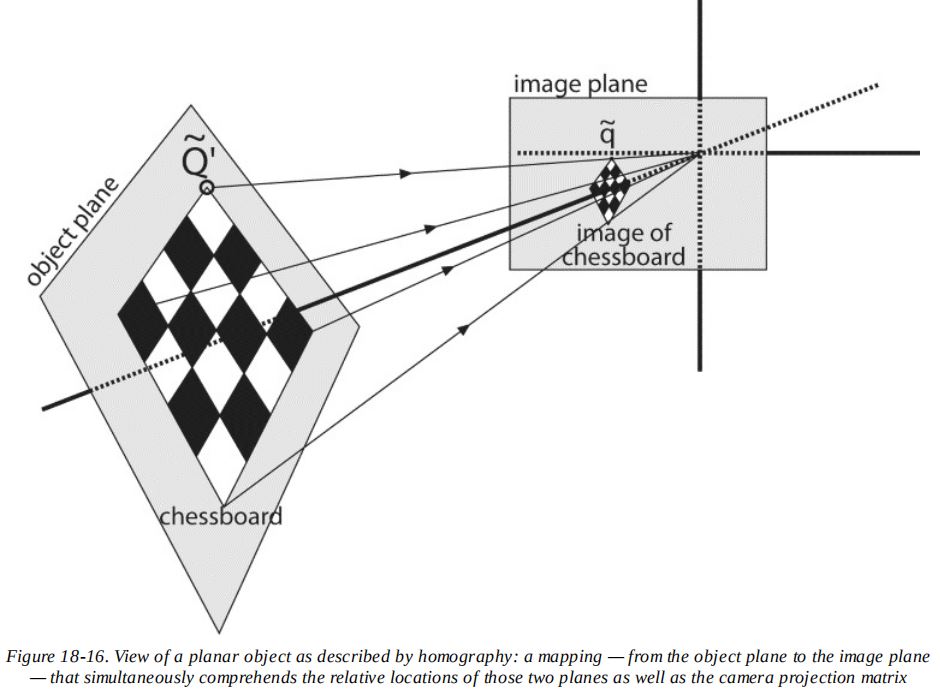
利用齐次坐标，可以对物理世界的点Q到成像画面上的点q的映射进行表示：

$$q=s\cdot M\cdot W\cdot Q$$
其中，参数s表示尺度比例，$M=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$ ，W表示旋转R和平移t的影响之和$W=[Rt]$，旋转矩阵$R=\left[\begin{array}{ccc}\overrightarrow{r_1}& \overrightarrow{r_2}& \overrightarrow{r_3}\end{array}\right]$

由于我们只关注这个物体平面，为了简化计算，令Z=0：
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=s\cdot M\cdot \left[\begin{array}{cccc}\overrightarrow{r_1}& \overrightarrow{r_2}& \overrightarrow{r_3}& \vec{t}\end{array}\right]\cdot [\begin{array}{c}OpenCV中的透视变换介绍\end{array}$$

（1-2）投影变换

OpenCV图像处理--平面单应性

findHomography(src_points, dst_points, CV_RANSAC)

如何计算两次透视变换后的结果？

利用OpenCV的函数warpPerspective()作图像的透视变换