激活函数汇总，包含公式求导过程以及numpy实现，妥妥的万字干货
Posted AI浩
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了激活函数汇总，包含公式求导过程以及numpy实现，妥妥的万字干货相关的知识，希望对你有一定的参考价值。
1、激活函数的实现
1.1 sigmoid
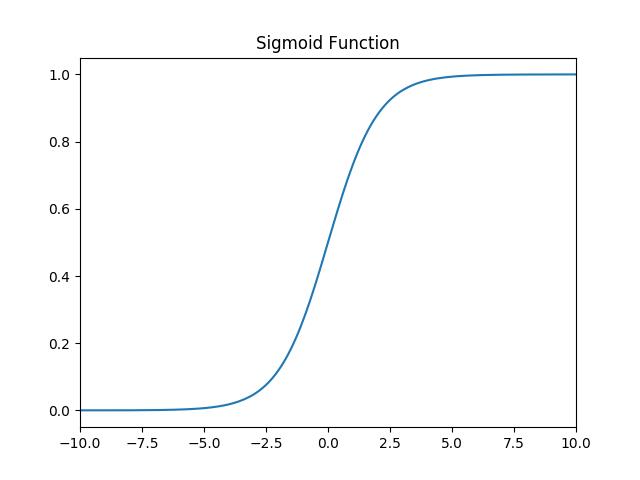
1.1.1 函数
函数： f ( x ) = 1 1 + e − x f(x)=\\frac{1}{1+e^{-x}} f(x)=1+e−x1
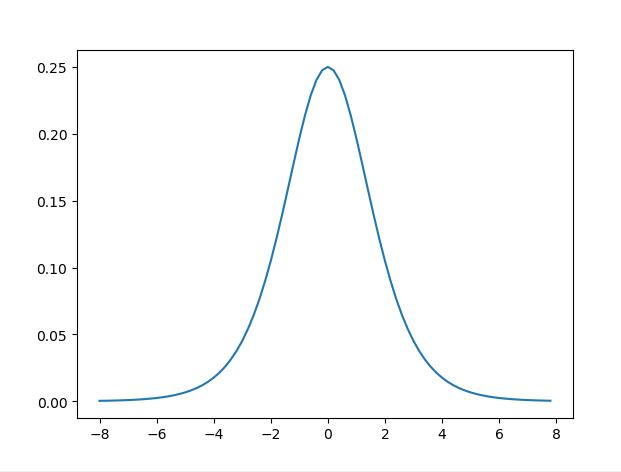
1.1.2 导数
求导过程：
根据：
(
u
v
)
′
=
u
′
v
−
u
v
′
v
2
\\left ( \\frac{u}{v} \\right ){}'=\\frac{{u}'v-u{v}'}{v^{2}}
(vu)′=v2u′v−uv′
f
(
x
)
′
=
(
1
1
+
e
−
x
)
′
=
1
′
×
(
1
+
e
−
x
)
−
1
×
(
1
+
e
−
x
)
′
(
1
+
e
−
x
)
2
=
e
−
x
(
1
+
e
−
x
)
2
=
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
(
1
1
+
e
−
x
)
(
1
−
1
1
+
e
−
x
)
=
f
(
x
)
(
1
−
f
(
x
)
)
\\begin{aligned} f(x)^{\\prime} &=\\left(\\frac{1}{1+e^{-x}}\\right)^{\\prime} \\\\ &=\\frac{1^{\\prime} \\times\\left(1+e^{-x}\\right)-1 \\times\\left(1+e^{-x}\\right)^{\\prime}}{\\left(1+e^{-x}\\right)^{2}} \\\\ &=\\frac{e^{-x}}{\\left(1+e^{-x}\\right)^{2}} \\\\ &=\\frac{1+e^{-x}-1}{\\left(1+e^{-x}\\right)^{2}} \\\\ &=\\left(\\frac{1}{1+e^{-x}}\\right)\\left(1-\\frac{1}{1+e^{-x}}\\right) \\\\ &=\\quad f(x)(1-f(x)) \\end{aligned}
f(x)′=(1+e−x1)′=(1+e−x)21′×(1+e−x)−1×(1+e−x)′=(1+e−x)2e−x=(1+e−x)21+e−x−1=(1+e−x1)(1−1+e−x1)=f(x)(1−f(x))
1.1.3 代码实现
import numpy as np
class Sigmoid():
def __call__(self, x):
return 1 / (1 + np.exp(-x))
def gradient(self, x):
return self.__call__(x) * (1 - self.__call__(x))
1.2 softmax
1.2.1 函数
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！
假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是:
S
i
=
e
i
∑
j
e
j
S_{i}=\\frac{e^{i}}{\\sum _{j}e^{j}}
Si=∑jejei
更形象的如下图表示：
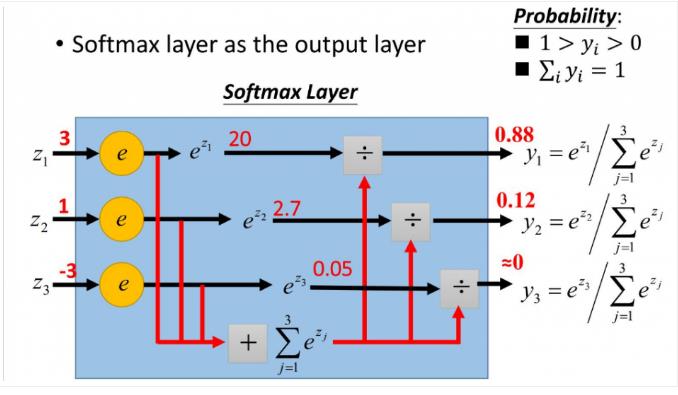
y
1
=
e
z
1
e
z
1
+
e
z
2
+
e
z
3
y
2
=
e
z
2
e
z
1
+
e
z
2
+
e
z
3
y
3
=
e
z
3
e
z
1
+
e
z
2
+
e
z
3
(1)
y1=\\frac{e^{z_{1}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}}\\\\ y2=\\frac{e^{z_{2}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}}\\\\ y3=\\frac{e^{z_{3}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}}\\\\ \\tag{1}
y1=ez1+ez2+ez3ez1y2=ez1+ez2+ez3ez2y3=ez1+e转载softmax的log似然代价函数（求导过程）