字典树(Trie树)

Posted 2021-10-03 文大侠

字典树主要是为了解决前缀匹配问题，比如下图的搜索输入前缀后匹配

比如有6个字符串how，hi，her，hello，so，see，如果现在输入字符判断是否要前缀匹配指定字符串，必须一个字符串比较，如果有100万就要比对100万次，如何优化这个问题呢？

其实我们可以理解，每输入一个字符，应该整个搜索空间就会缩小，具体来说就是构造一颗如下的树，就是所谓的字典树（Trie树），一旦构建完成，搜索过程中，即可完成动态剪裁，最大搜索次数就是最长字符串长度。

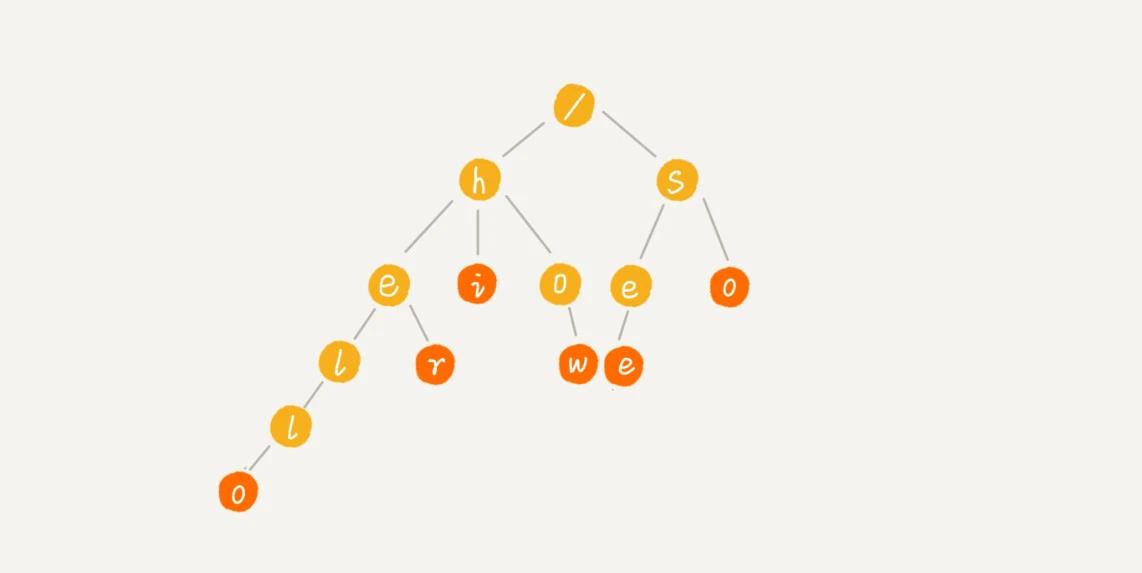
具体实现来说就是一颗多叉树，可以使用hashmap或者数组保存子节点指针。

如下是最常见的实现，对于确定的26个字母构成单词的trie树，可通过下标转换快速定位

public class Trie {
    public class TrieNode {
        public char data;
        public TrieNode[] link = new TrieNode[26];// 多叉树存储所有下级子节点(26个字母)
        public boolean isEndingChar = false; // 标记当前点是否为字符串结束点，判断是否完全匹配

        public TrieNode(char c) {
            this.data = c;
        }
    }

    TrieNode root;

    /**
     * Initialize your data structure here.
     */
    public Trie() {
        root = new TrieNode('/');
    }

    /**
     * Inserts a word into the trie.
     */
    public void insert(String word) {
        TrieNode p = root;

        for (int i = 0; i < word.length(); i++) {
            int linki = word.charAt(i) - 'a';
            if (p.link[linki] == null) {// 不存在
                p.link[linki] = new TrieNode(word.charAt(i));
            }

            p = p.link[linki];
        }

        p.isEndingChar = true;
    }

    /**
     * Returns if the word is in the trie.
     */
    public boolean search(String word) {
        TrieNode p = root;

        for (int i = 0; i < word.length(); i++) {
            int linki = word.charAt(i) - 'a';
            if (p.link[linki] == null) {// 不存在
                return false;
            }

            p = p.link[linki];
        }

        return p.isEndingChar; // true 完全匹配/ false 前缀匹配，不是完全匹配
    }

    /**
     * Returns if there is any word in the trie that starts with the given prefix.
     */
    public boolean startsWith(String prefix) {
        TrieNode p = root;

        for (int i = 0; i < prefix.length(); i++) {
            int linki = prefix.charAt(i) - 'a';
            if (p.link[linki] == null) {// 不存在
                return false;
            }

            p = p.link[linki];
        }

        return true;
    }

    /**
     * 获取指定前缀匹配的列表
     *
     * @param prefix
     * @return
     */
    public String[] getPrefixList(String prefix) {
        ArrayList<String> ret = new ArrayList<>();

        TrieNode p = root;

        for (int i = 0; i < prefix.length(); i++) {
            int linki = prefix.charAt(i) - 'a';
            if (p.link[linki] == null) {// 不存在
                return ret.toArray(new String[]{});
            }

            p = p.link[linki];
        }

        getFullStringFromNode(ret, prefix, p);
        return ret.toArray(new String[]{});
    }

    public void getFullStringFromNode(ArrayList<String> ret, String prefix, TrieNode p) {
        if (p.isEndingChar) {
            ret.add(prefix);
        }

        for (int i = 0; i < p.link.length; i++) {
            if (p.link[i] != null) {
                getFullStringFromNode(ret, prefix + p.link[i].data, p.link[i]);
            }
        }
    }
}

这里有很多优化空间，比如不是26个字母时如何处理，通常采用hashmap/treemap/skiplist都可以来优化空点带来的额外开销，比如使用hashmap优化这个过程，思想都差不多

type TrieNode struct {
	data         byte
	link         map[byte]*TrieNode // 多叉树存储所有下级子节点(26个字母)
	isEndingChar bool               // 标记当前点是否为字符串结束点，判断是否完全匹配
}

func getTrieNode(c byte) *TrieNode {
	return &TrieNode{c, make(map[byte]*TrieNode), false}
}

type Trie struct {
	root *TrieNode
}

/** Initialize your data structure here. */
func Constructor() Trie {
	return Trie{getTrieNode('/')}
}

/** Inserts a word into the trie. */
func (this *Trie) Insert(word string) {
	p := this.root

	for _, v := range []byte(word) {
		if _, ok := p.link[v]; !ok { // 不存在
			p.link[v] = getTrieNode(v)
		}

		p = p.link[v]
	}

	p.isEndingChar = true
}

/** Returns if the word is in the trie. */
func (this *Trie) Search(word string) bool {
	p := this.root

	for _, v := range []byte(word) { // 不存在
		if _, ok := p.link[v]; !ok {
			return false
		}

		p = p.link[v]
	}

	return p.isEndingChar
}

/** Returns if there is any word in the trie that starts with the given prefix. */
func (this *Trie) StartsWith(prefix string) bool {
	p := this.root

	for _, v := range []byte(prefix) {
		if _, ok := p.link[v]; !ok { // 不存在
			return false
		}

		p = p.link[v]
	}

	return true
}

func (this *Trie) GetPrefixList(prefix string) []string {
	ret := make([]string, 0)

	p := this.root

	for _, v := range []byte(prefix) {
		if _, ok := p.link[v]; !ok { // 不存在
			return ret
		}

		p = p.link[v]
	}

	// 匹配前缀后遍历输出全部匹配
	var getFullStringFromNode func(prefix string, p *TrieNode)
	getFullStringFromNode = func(prefix string, p *TrieNode) {
		if p.isEndingChar {
			ret = append(ret, prefix)
		}

		for _, v := range p.link {
			getFullStringFromNode(fmt.Sprintf("%s%c", prefix, v.data), v)
		}
	}

	getFullStringFromNode(prefix, p)
	return ret
}

• 源代码位置 https://github.com/JimWen/go-algo/tree/main/trie

原创，转载请注明来自

• 博客https://blog.csdn.net/wenzhou1219
• 个人网站http://jimwen.net/