二叉树_review

Posted 2021-10-03 黑桃_K_

二叉树

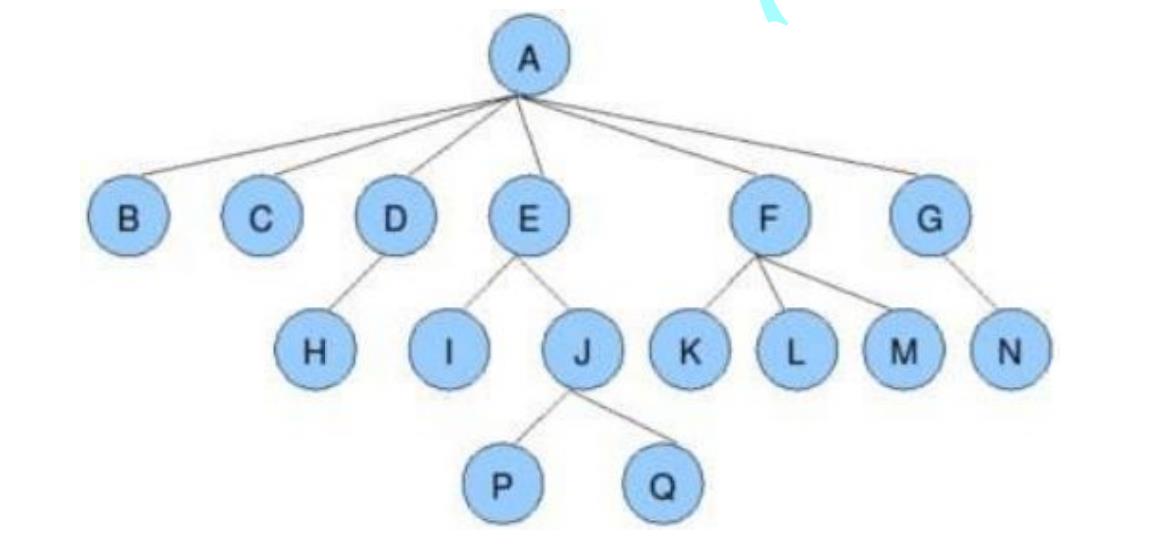
• 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6 比特科技
• 叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点
• 非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点
• 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
• 兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点
• 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
• 树的高度或深度：树中节点的最大层次； 如上图：树的高度为4
• 堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
• 节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
• 森林：由m（m>0）棵互不相交的树的集合称为森林；

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

特殊的二叉树

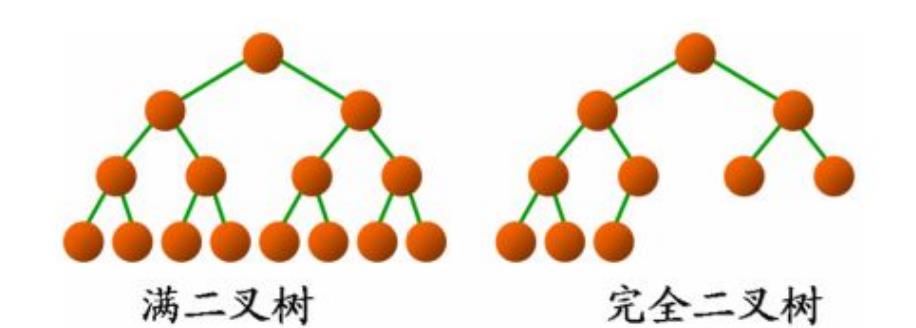
1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。
2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h- 1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0＝n2＋1
4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=Log2(n+1). (ps：Log2(n+1)是log以2为
   底，n+1为对数)
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对
   于序号为i的结点有：
6. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
7. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
8. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

typedef int DataType;
struct Node
{
 struct Node* _firstChild1; // 第一个孩子结点
 struct Node* _pNextBrother; // 指向其下一个兄弟结点
 DataType _data; // 结点中的数据域
};

#include<stdlib.h>
#include<stdio.h>
#include<iostream>
#include<queue>
#include<list>
using namespace std;
typedef char BTDataType; 

typedef struct BTNode{
	BTDataType _data;
	struct BTNode* _left;
	struct BTNode* _right;
}BTNode;
//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* arr, int* index){
	if (arr[*index] == '#'){
		++(*index);
		return NULL;
	}
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->_data = arr[*index];  
	++(*index);
	root->_left = BinaryTreeCreate(arr, index);
	root->_right = BinaryTreeCreate(arr, index);
	return root;
}
//前序遍历
void preOrder(BTNode* root){
	if (root){
		//根   左  右
		printf("%c", root->_data);
		preOrder(root->_left);
		preOrder(root->_right);
	}
}
//中序遍历
void inOrder(BTNode* root){
	if (!root)
		return;
	//左    根    右
	inOrder(root->_left);
	printf("%c", root->_data);
	inOrder(root->_right);
}
//后序遍历
void postOrder(BTNode* root){
	if (!root)
		return;
	//左    右    根
	postOrder(root->_left);
	postOrder(root->_right);
	printf("%c", root->_data);
}
//节点个数
int BTSize(BTNode* root){
	if (!root)
		return 0;
	int left = BTSize(root->_left);
	int right = BTSize(root->_right);
	return left + right + 1;
}
//叶子节点
int BTLeafSize(BTNode* root){
	if (!root)
		return 0;
	if ((root->_left == NULL) && (root->_right == NULL))
		return 1;
	return BTLeafSize(root->_left) + BTLeafSize(root->_right);
}
//第k层节点个数
int BTLayerSize(BTNode* root,int K){
	if (!root)
		return 0;
	if (K == 1)
		return 1;
	return BTLayerSize(root->_left, K - 1)
		+ BTLayerSize(root->_right, K - 1);
}
//查找
BTNode* BTFind(BTNode* root, BTDataType ch){
	BTNode* node;
	if (root == NULL)
		return NULL;
	if (root->_data == ch)
		return root;
	node = BTFind(root->_left, ch);
	if (node)
		return node;
	return BTFind(root->_right, ch);
}
//销毁  不会有野指针
void BTDestroy(BTNode** root){
	if (*root){
		BTDestroy(&((*root)->_left));
		BTDestroy(&((*root)->_right));
		free(*root);
		*root = NULL;
	}
}
//销毁 会有野指针
void BTDestroy2(BTNode* root){
	if (root){
		BTDestroy2(root->_left);
		BTDestroy2(root->_right);
		free(root);//root为拷贝指针，赋值为NULL真的指针指向不变，二级指针赋值NULL才可以，
		//不赋值为空，就会出现野指针
	}
}
//层序遍历
void BTLevelOrder(BTNode* root){
	queue<BTNode*> q;
	if (root)
	q.push(root);
	while (!q.empty()){
		BTNode* node = q.front();
		cout << node->_data;
		if (node->_left)
		q.push(node->_left);
		if (node->_right)
		q.push(node->_right);
		q.pop();
	}
}
//判断是否是完全二叉树
int isCompleteBT(BTNode* root){
	queue<BTNode*> q;
	if (root)
		q.push(root);
	while (!q.empty()){
		BTNode* node = q.front();
		q.pop();
		if (node){
			q.push(node->_left);
			q.push(node->_right);
		}
		else
			break;
	}
	while (!q.empty()){
		BTNode* node = q.front();
		q.pop();
		if (node)
			return 0;
	}
	return 1;
}
//判断是否是完全二叉树  list
int isCompleteBT2(BTNode* root){
	list<BTNode*> lst;
	if (root)
		lst.push_back(root);
	while (!lst.empty()){
		BTNode* node = lst.front();
		lst.pop_front();
		if (node){
			lst.push_back(node->_left);
			lst.push_back(node->_right);
		}
		else
			break;
	}
	while (!lst.empty()){
		BTNode* node = lst.front();
		lst.pop_front();
		if (node)
			return 0;
	}
	return 1;
}
void test(){
	char arr[] = "ABDH###E##CF##G##";
	int index = 0;
	BTNode* root = BinaryTreeCreate(arr, &index);
	preOrder(root);
	cout << endl;
	inOrder(root);
	cout << endl;
	postOrder(root);
	cout << endl;
	BTLevelOrder(root);
	cout << endl;
	int flag=isCompleteBT(root);
	if (flag)
		cout << "yes" << endl;
	else
		cout << "NO" << endl;

	if (isCompleteBT2(root))
		cout << "YES" << endl;
	else
		cout << "NO" << endl;
}


int main(){
	test();
	return 0;
}
//34