数据结构与算法2(LeetCode)
Posted 康x呀
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法2(LeetCode)相关的知识,希望对你有一定的参考价值。
数据结构与算法2(LeetCode)
344. 反转字符串
OJ链接:https://leetcode-cn.com/problems/reverse-string/
题目:编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:[“h”,“e”,“l”,“l”,“o”]
输出:[“o”,“l”,“l”,“e”,“h”]
示例 2:
输入:[“H”,“a”,“n”,“n”,“a”,“h”]
输出:[“h”,“a”,“n”,“n”,“a”,“H”]
代码:
思路简单,先写一个交换的函数,然后利用双指针法再去调用即可
// An highlighted block
void swap(char *a, char *b)
{
char t = *a;
*a = *b, *b = t;
}
void reverseString(char *s, int sSize)
{
for (int left = 0, right = sSize - 1; left < right; ++left, --right)
{
swap(s + left, s + right);
}
}
557. 反转字符串中的单词 III
OJ链接:https://leetcode-cn.com/problems/reverse-words-in-a-string-iii/
题目:给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例:
输入:“Let’s take LeetCode contest”
输出:“s’teL ekat edoCteeL tsetnoc”
代码:
**方法一:使用额外空间**
开辟一个新字符串,然后从头到尾遍历原字符串,直到找到空格为止,此时找到了一个单词,并能得到单词的起止
位置随后,根据单词的起止位置,可以将该单词逆序放到新字符串当中。如此循环多次,直到遍历完原字符串,就
能得到翻转后的结果。
// An highlighted block
char* reverseWords(char* s)
{
int length = strlen(s);
char* ret = (char*)malloc(sizeof(char) * (length + 1));
ret[length] = 0;
int i = 0;
while (i < length)
{
int start = i;
while (i < length && s[i] != ' ')
{
i++;
}
for (int p = start; p < i; p++)
{
ret[p] = s[start + i - 1 - p];
}
while (i < length && s[i] == ' ')
{
ret[i] = ' ';
i++;
}
}
return ret;
}
方法二:原地解法
此题也可以直接在原字符串上进行操作,避免额外的空间开销。当找到一个单词的时候,我们交换字符串第一个字符
与倒数第一个字符,随后交换第二个字符与倒数第二个字符……如此反复,就可以在原空间上翻转单词。
// An highlighted block
char* reverseWords(char* s)
{
int length = strlen(s);
int i = 0;
while (i < length)
{
int start = i;
while (i < length && s[i] != ' ')
{
i++;
}
int left = start, right = i - 1;
while (left < right)
{
char tmp = s[left];
s[left] = s[right], s[right] = tmp;
left++;
right--;
}
while (i < length && s[i] == ' ')
{
i++;
}
}
return s;
}
19. 删除链表的倒数第 N 个结点
OJ链接:https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/
题目:给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
代码:
一种容易想到的方法是,我们首先从头节点开始对链表进行一次遍历,得到链表的长度 L。随后
我们再从头节点开始对链表进行一次遍历,当遍历到第 L-n+1 个节点时,它就是我们需要删除的
节点。
为了与题目中的 n 保持一致,节点的编号从 1 开始,头节点为编号 1的节点。
为了方便删除操作,我们可以从哑节点开始遍历 L-n+1个节点。当遍历到第 L-n+1 个节点时,
它的下一个节点就是我们需要删除的节点,这样我们只需要修改一次指针,就能完成删除操作。
// An highlighted block
int getLength(struct ListNode* head) {
int length = 0;
while (head) {
++length;
head = head->next;
}
return length;
}
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
struct ListNode* dummy = malloc(sizeof(struct ListNode));
dummy->val = 0, dummy->next = head;
int length = getLength(head);
struct ListNode* cur = dummy;
for (int i = 1; i < length - n + 1; ++i) {
cur = cur->next;
}
cur->next = cur->next->next;
struct ListNode* ans = dummy->next;
free(dummy);
return ans;
}
方法二:栈
思路与算法:
我们也可以在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则,我们弹出栈的
第 n个节点就是需要删除的节点,并且目前栈顶的节点就是待删除节点的前驱节点。这样一来,
删除操作就变得十分方便了。
// An highlighted block
struct Stack {
struct ListNode* val;
struct Stack* next;
};
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
struct ListNode* dummy = malloc(sizeof(struct ListNode));
dummy->val = 0, dummy->next = head;
struct Stack* stk = NULL;
struct ListNode* cur = dummy;
while (cur) {
struct Stack* tmp = malloc(sizeof(struct Stack));
tmp->val = cur, tmp->next = stk;
stk = tmp;
cur = cur->next;
}
for (int i = 0; i < n; ++i) {
struct Stack* tmp = stk->next;
free(stk);
stk = tmp;
}
struct ListNode* prev = stk->val;
prev->next = prev->next->next;
struct ListNode* ans = dummy->next;
free(dummy);
return ans;
}
双指针法:
// An highlighted block
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
struct ListNode* dummy = malloc(sizeof(struct ListNode));
dummy->val = 0, dummy->next = head;
struct ListNode* first = head;
struct ListNode* second = dummy;
for (int i = 0; i < n; ++i) {
first = first->next;
}
while (first) {
first = first->next;
second = second->next;
}
second->next = second->next->next;
struct ListNode* ans = dummy->next;
free(dummy);
return ans;
}
3. 无重复字符的最长子串
OJ链接:https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/
题目:给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
示例 4:
输入: s = " "
输出: 0
代码:
首先对特殊状况进行判断。大体思路就是要利用一个数组来记录各个字符出现的个数。在循环中右指针先走,标记
出现过的字符。如果字符出现的次数大于2,即重复出现,就该指针之前的所有字符的出现次数清除,左指针移动到
右指针处重新计数。
// An highlighted block
int lengthOfLongestSubstring(char * s){
int len = strlen(s);
if(len == 0 || len == 1)
return len;
int left = 0;
int right = 0;
int S[256] = {0};//先全部赋初值位0
int ans=0;
while(right<len)
{
S[s[right]]++;
while(S[s[right]]>1)
{
S[s[left]]--;
left++;
}
ans = fmax(ans,right-left+1);
right++;
}
return ans;
}
567. 字符串的排列
OJ链接:https://leetcode-cn.com/problems/permutation-in-string/
题目:给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,s1 的排列之一是 s2 的 子串 。
示例 1:
输入:s1 = “ab” s2 = “eidbaooo”
输出:true
解释:s2 包含 s1 的排列之一 (“ba”).
示例 2:
输入:s1= “ab” s2 = “eidboaoo”
输出:false
代码:
双指针法:
// An highlighted block
bool checkInclusion(char* s1, char* s2)
{
int n = strlen(s1), m = strlen(s2);
if (n > m)
{
return false;
}
int cnt[26];
memset(cnt, 0, sizeof(cnt));
for (int i = 0; i < n; ++i)
{
--cnt[s1[i] - 'a'];
}
int left = 0;
for (int right = 0; right < m; ++right)
{
int x = s2[right] - 'a';
++cnt[x];
while (cnt[x] > 0)
{
--cnt[s2[left] - 'a'];
++left;
}
if (right - left + 1 == n)
{
return true;
}
}
return false;
}
21. 合并两个有序链表
OJ链接:https://leetcode-cn.com/problems/merge-two-sorted-lists/
题目:将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
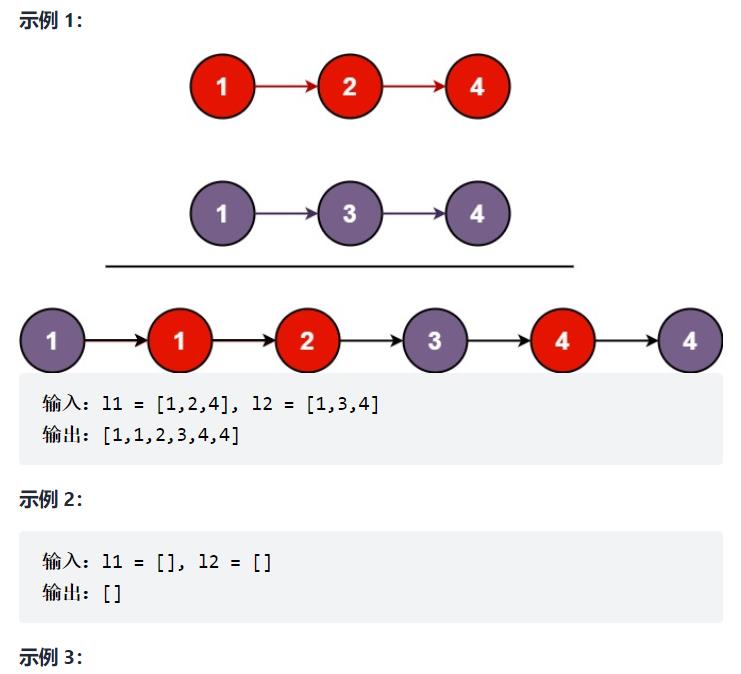
输入:l1 = [], l2 = [0]
输出:[0]
代码:
我们直接将以上递归过程建模,同时需要考虑边界情况。
如果 l1 或者 l2 一开始就是空链表 ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们
要判断 l1 和 l2 哪一个链表的头节点的值更小,然后递归地决定下一个添加到结果里的节点。如果两个链表有
一个为空,递归结束。
// An highlighted block
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2)
{
if (l1 == NULL)
{
return l2;
}
else if (l2 == NULL)
{
return l1;
}
else if (l1->val < l2->val)
{
l1->next = mergeTwoLists(l1->next, l2);
return l1;
}
else
{
l2->next = mergeTwoLists(l1, l2->next);
return l2;
}
}
617. 合并二叉树
OJ链接:https://leetcode-cn.com/problems/merge-two-binary-trees/
题目:给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
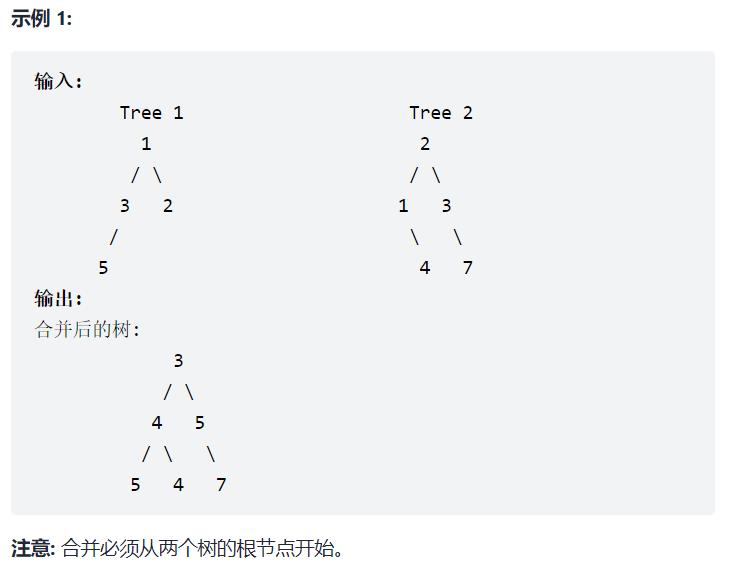
代码:
可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树,并将对应的节点进行合并。
两个二叉树的对应节点可能存在以下三种情况,对于每种情况使用不同的合并方式。
如果两个二叉树的对应节点都为空,则合并后的二叉树的对应节点也为空;
如果两个二叉树的对应节点只有一个为空,则合并后的二叉树的对应节点为其中的非空节点;
如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和,
此时需要显性合并两个节点。对一个节点进行合并之后,还要对该节点的左右子树分别进行合并。这是一个
递归的过程。
// An highlighted block
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode* mergeTrees(struct TreeNode* t1, struct TreeNode* t2)
{
if (t1 == NULL)
{
return t2;
}
if (t2 == NULL)
{
return t1;
}
struct TreeNode* merged = malloc(sizeof(struct TreeNode));
merged->val = t1->val + t2->val;
merged->left = mergeTrees(t1->left, t2->left);
merged->right = mergeTrees(t1->right, t2->right);
return merged;
free(merged);
}
116.填充每个节点的下一个右侧节点指针
OJ链接:https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/
题目:给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
代码:
思路与算法
题目本身希望我们将二叉树的每一层节点都连接起来形成一个链表。因此直观的做法我们可以对二叉树进行层次遍历
,在层次遍历的过程中将我们将二叉树每一层的节点拿出来遍历并连接。
层次遍历基于广度优先搜索,它与广度优先搜索的不同之处在于,广度优先搜索每次只会取出一个节点来拓展,而层
次遍历会每次将队列中的所有元素都拿出来拓展,这样能保证每次从队列中拿出来遍历的元素都是属于同一层的,因
此我们可以在遍历的过程中修改每个节点的 \\text{next}next 指针,同时拓展下一层的新队列。
// An highlighted block
/**
* Definition for a Node.
* struct Node {
* int val;
* struct Node *left;
* struct Node *right;
* struct Node *next;
* };
*/
struct Node* connect(struct Node* root)
{
if (root == NULL)
{
return root;
}
// 初始化队列同时将第一层节点加入队列中,即根节点
struct Node* Q[5000];
int left = 0, right = 0;
Q[right++] = root;
// 外层的 while 循环迭代的是层数
while (left < right)
{
// 记录当前队列大小
int size = right - left;
// 遍历这一层的所有节点
for (int i = 0; i < size; i++)
{
// 从队首取出元素
struct Node* node = Q[left++];
// 连接
if (i < size - 1)
{
node->next = Q[left];
}
// 拓展下一层节点
if (node->left != NULL)
{
Q[right++] = node->left;
}
if (node->right != NULL)
{
Q[right++] = node->right;
}
}
}
// 返回根节点
return root;
}
70. 爬楼梯
OJ链接:https://leetcode-cn.com/problems/climbing-stairs/
题目:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
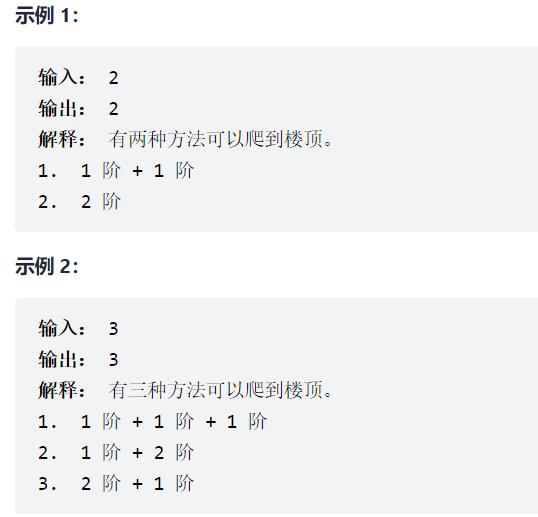

代码:
动态规划代码
// An highlighted block
int climbStairs(int n)
{
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
120. 三角形最小路径和
OJ链接:https://leetcode-cn.com/problems/triangle/
题目:给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。


代码:
具体代码实现如下:
// An highlighted block
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize)
{
int f[triangleSize][triangleSize];
memset(f, 0, sizeof(f));
f[0][0] = triangle[0][0];
for (int i = 1; i < triangleSize; ++i)
{
f[i][0] = f[i - 1][0] + triangle[i][0];
for (int j = 1; j < i; ++j)
{
f[i][j] = fmin(f[i - 1