07堆排序 python

Posted 2021-10-02 炫云云

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了07堆排序 python相关的知识，希望对你有一定的参考价值。

文章目录

05 归并排序

06快速排序算法

07堆排序python

堆

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。

堆实际上是一个完全二叉树结构。问：那么什么是完全二叉树呢？答：假设一个二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树

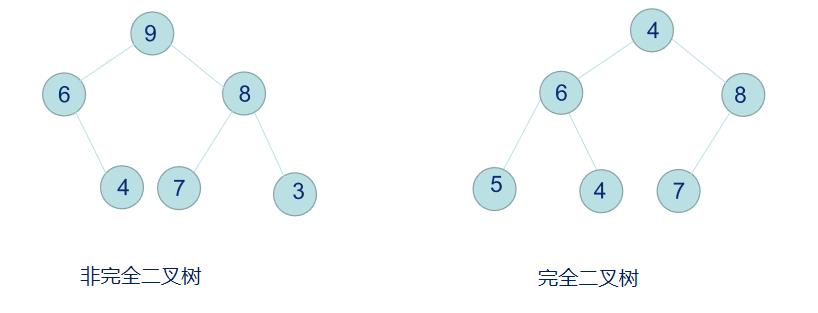
堆的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

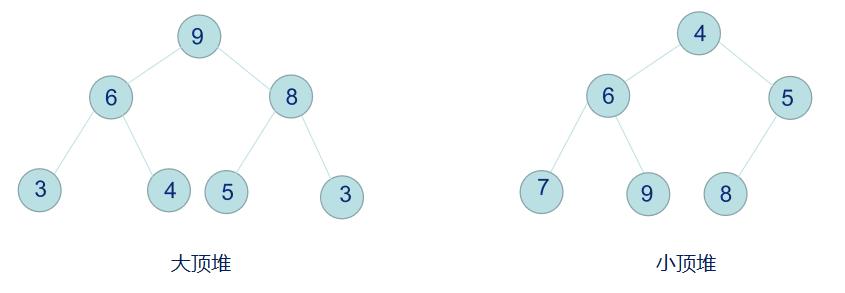
大顶堆：每个节点的值都大于或等于其子节点的值: Key[i] >= Key[2i+1] && key >= key[2i+2]，在堆排序算法中用于升序排列；
小顶堆：每个节点的值都小于或等于其子节点的值: Key[i] <= key[2i+1] && Key[i] <= key[2i+2]，在堆排序算法中用于降序排列；

我们来看看大顶堆和小顶堆的示意图:

堆排序算法

我们来看下堆排序的思想是怎样的(以大根堆为例)：

首先将待排序的数组构造出一个大根堆
取出这个大根堆的堆顶节点(最大值)，与堆的最下最右的元素进行交换，然后把剩下的元素再构造出一个大根堆
重复第二步，直到这个大根堆的长度为1，此时完成排序。

下面通过图片来看下，第二个步骤是如何进行的：

动图演示

代码

class Solution(object):
    def heap_sort(self, arr):
        n = len(arr) 
        self.buildHeap(arr, n)
        # 上面的循环完成了大顶堆的构造，那么就开始把根节点跟末尾节点交换，
        # 然后重新调整大顶堆  
        for i in range(n-1, -1, -1):
            arr[0], arr[i] = arr[i], arr[0] #根节点跟末尾节点交换
            self.heapify(arr, i, 0)

    def buildHeap(self,arr, heapsize):
        # 构造大顶堆，从非叶子节点开始倒序遍历，因此是heapsize // 2 - 1就是最后一个非叶子节点
        for i in range(heapsize // 2 - 1, -1, -1):
            self.heapify(arr, heapsize,i)


    def heapify(self,arr, n, i): 
        """调整大顶堆"""
        largest = i  
        # 左右子节点的下标
        l = 2 * i + 1     # left = 2*i + 1 
        r = 2 * i + 2     # right = 2*i + 2
        if l < n and arr[i] < arr[l]: 
            largest = l 
    
        if r < n and arr[largest] < arr[r]: 
            largest = r 
        # 通过上面跟左右节点比较后，得出三个元素之间较大的下标，
        # 如果较大下表不是父节点的下标，说明交换后需要重新调整大顶堆
        if largest != i: 
            arr[i],arr[largest] = arr[largest],arr[i]  # 交换
            self.heapify(arr, n, largest) 

arr = [ 12, 11, 13, 5, 6, 7] 
S = Solution()
S.heap_sort(arr) 
n = len(arr) 
print ("排序后") 
for i in range(n): 
    print ("%d" %arr[i])

堆排序复杂度

时间复杂度，包括两个方面：

初始化建堆过程时间： $O (n)$
更改堆元素后重建堆时间： $O (n l o g n)$ ，循环 n -1 次，每次都是从根节点往下循环查找，所以每一次时间是 $l o g n$ ，总时间： $l o g n (n - 1) = n l o g n - l o g n$ ，所以复杂度是 $O (n l o g n)$

时间复杂度： $O (n l o g n)$ 空间复杂度：因为堆排序是就地排序，空间复杂度为常数： $O (1)$

堆排序的应用：TopK算法

如果在海量数据中找出最大的100个数字，看到这个问题，可能大家首先会想到的是使用高效排序算法，比如快排，对这些数据排序，时间复杂度是O(nlogn)，然后取出最大的100个数字。但是如果数据量很大，一个机器的内存不足以一次过读取这么多数据，就不能使用这个方法了。

不使用分布式机器计算，使用一个机器也能找出TopK的经典算法就是使用堆排序了，具体方法是：

维护一个大小为 K 的小顶堆，依次将数据放入堆中，当堆的大小满了的时候，只需要将堆顶元素与下一个数比较：

如果小于堆顶元素，则直接忽略，比较下一个元素；
如果大于堆顶元素，则将当前的堆顶元素抛弃，并将该元素插入堆中。遍历完全部数据，Top K 的元素也自然都在堆里面了。

整个操作中，遍历数组需要 $O (n)$ 的时间复杂度，每次调整小顶堆的时间复杂度是 $O (l o g K)$ ，加起来就是 $O (n l o g K)$ 的复杂度，如果 $K$ 远小于 $n$ 的话， $O (n l o g K)$ 其实就接近于 $O (n)$ 了，甚至会更快，因此也是十分高效的。