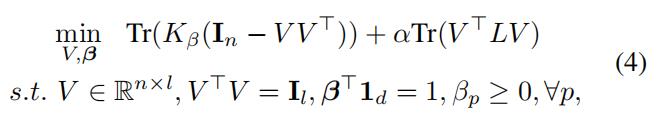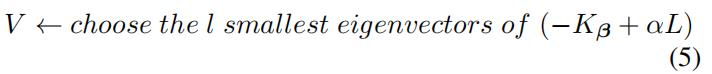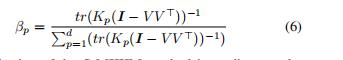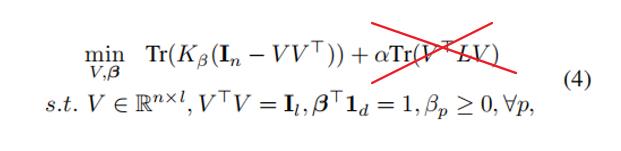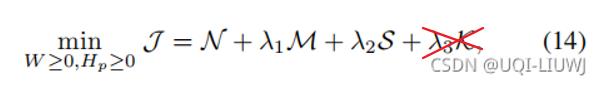论文笔记:Missing Value Imputation for Multi-view UrbanStatistical Data via Spatial Correlation Learning
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文笔记:Missing Value Imputation for Multi-view UrbanStatistical Data via Spatial Correlation Learning相关的知识,希望对你有一定的参考价值。
TKDE 2021(Apr)
0 摘要
作为城市化的发展趋势,海量的多视角(如人口和经济视角)的城市统计数据被越来越多地收集并受益于不同领域,包括交通服务、区域分析等。
划分为细粒度区域的数据在获取和存储过程中通常会遇到缺失值问题。这主要是由于一些不可避免的情况造成的,例如文件污损、偏远地区统计困难、信息清理不准确等。那些使有价值信息不可见的缺失条目可能会扭曲进一步的城市分析。
为了提高缺失数据插补的质量,我们提出了一种改进的空间多核学习方法,结合自适应权重非负矩阵分解策略来指导交通插补过程(traffic imputation)。我们的X模型考虑了区域潜在相似性和真实地理位置以及能够精确完成缺失值的各种视图之间的相关性。
我们进行了大量实验来评估我们的方法,并在现实世界的数据集上与其他最先进的方法进行比较。所有的实证结果表明,所提出的模型优于所有其他最先进的方法。此外,我们的模型代表了跨多个城市的强大泛化能力。
1 introduction
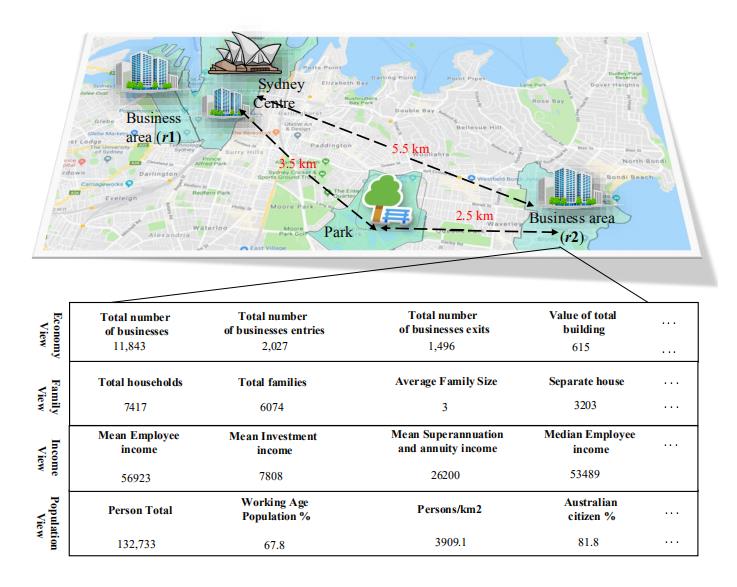
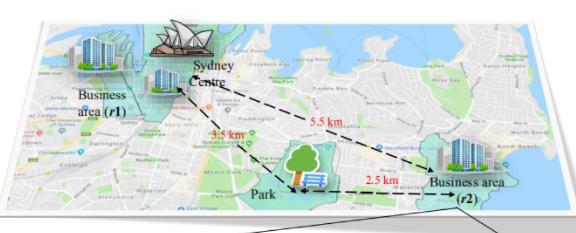
图1是一个多视角区域统计结果
区域r2包括了四个不同视角的数据:经济、家庭、人口、收入
这种统计数据是很重要的。但是在一些地方,因为数据收集、储存等一些原因,统计数据并不能完全得到,这就导致了数据缺失和数据稀疏的问题。
这些数据缺失和稀疏的问题会导致分析结果有可能偏离实际情况。比如在POI 推荐中,经济和人口是两个主要的决定因素,如果一个区域经济维度的属性缺失甚多,那么很大概率POI推荐会根据人口的聚集情况进行推荐,因为它基本上只能考虑人口这一个维度的属性。
因此,一个对于城市统计数据的补全模型是需要,而且是重要的。
在这篇论文中,我们探索了澳洲统计局ABS和新西兰统计局NZS提供的城市统计数据中的确实数据补全问题。
这种多视图城市统计数据的缺失值插补任务比完成其他数据集的缺失值要困难得多,因为这类问题有一些独特的挑战:
- 空间关联性的挖掘
不同区域的统计数据可能因为地点的不同而显著而又非线性地变化,因此,潜在的空间关联性需要在分析空间相关的数据中进行考虑。
因此,为了合适地恢复统计数据的丢失信息,我们需要较为精准地考虑空间相似性。
在图1中,我们会发现,区域r1和悉尼歌剧院的属性是很相似的,因为它们是挨着的;
与此同时,尽管区域r2和空间在物理空间上是更近的,但是由于r2和悉尼歌剧院有相似的功能属性,所以r2和悉尼歌剧院的属性相似。
- 多维度属性关联性的问题
如果我们只是简单地分别恢复缺失的信息,而不考虑各个属性之间的关联性,那么我们的模型最终不一定会有很好的表现。
打个比方,经济相关的属性(economy),通常和收入(income)、人口(population)属性有着强关联(经济高的区域通常收入好人口多)。如果我们只是分别考虑经济、收入和人口,而不考虑它们的关联性的话,那么不一定会有很好的补全结果。
因此,如何整合各个维度的数据,是一个核心的问题
- 时间信息的缺失
在这类问题中,今年缺失的数据,去年、前年一样缺失。这可能由于区域数据收集的限制或者其他一些原因。
基于这个现象,时间维度的特点是无法建模得到的。
同时,这一种情况也不符合矩阵补全的最基本假设:没有观测到的内容是在一个完整的矩阵中随机取出的。
因此,基于矩阵补全任务的方法可能不能很好地工作。
这几年,尽管有一些方法(mean-filling,KNN)在单维度数据补全问题上有不俗的表现,但是他们在多维度数据补全问题上表现不佳,尤其当引入空间属性之后。
与此同时,尽管一些时空数据挖掘的方法可以基于时间和空间的知识,推断出缺失的信息,但是如果遇到前面说的“时间信息的缺失”问题,它们的表现也不理想。
为了很好地应对所有挑战,我们通过空间相关性学习设计了一个模型。 具体而言,该方法集成了空间多核聚类方法和自适应权重非负矩阵分解(NMF)方法来解决多视图空间相关任务。
本文的贡献如下:
- 为了解决具有空间特征的多视图问题,我们设计了一种空间相关的多核 K 均值 (S-MKKM) 方法来识别多视图之间的潜在关系并捕获区域相似性。
- 我们提出了一种自适应权重非负矩阵分解方法,以利用上面学到的信息来解决多视图缺失数据插补问题。 此外,所提出的方法还考虑了单视图信息补全模型的特点,同时考虑了 KNN 策略来利用真实地理信息。
- 提出了一种基于空间相关性学习的城市统计数据多视图缺失数据插补方法,称为SMV-NMF。 SMV-NMF 不依赖于时间信息,而是通过仅使用空间信息实现了很好的性能。
- 我们对六个真实世界的数据集进行了一系列实验,以证明我们的方法与其他最先进模型相比的有效性。 所有的评估结果表明,所提出的方法 SMV-NMF 产生了最好的性能。 此外,SMV-NMF 显示出强大的泛化能力,可以很好地将构建的模型从一个城市数据集转移到另一个。
2 相关工作
2.1 时空数据中的丢失数据补全问题
在空间相关领域,使用 邻居和协同过滤的方法是两种主要的填充缺失值的方法。
尽管一些传统的补全方法(比如补零、均值填充、回归模型)可以被应用在数据补全问题中,但他们并不能很好地适配空间数据问题
【21】使用距离的倒数加权(IDW inverse distance weighting)方法对空间降雨分布进行插值。(“Estimation of the spatial rainfall distribution using inverse distance weighting (idw) in the middle of taiwan,”)
【22】利用空间信息作为残差克里金法(residual kriginf)的输入来估计月平均温度。(
“Spatial interpolation of temperature in the united states using residual kriging,”)
不像空间模型,一些成功的时空模型被提出用于时间流数据
[8]开发了一种时空多视图方法 (ST-MVL) 来共同完成地理传感时间序列数据集合中的缺失值。 它考虑了
1) 同一时间序列中不同时间跨度的读数之间的时间相关性
2) 不同时间序列之间的空间相关性。
然而,他们通过考虑空间和时间属性来填充缺失的条目,在没有时间信息的静态空间数据上表现不佳。 此外,这种方法没有考虑多视图数据集的问题。
(“St-mvl: fifilling missing values in geo-sensory time series data.” IJCAI 2016)
在这里,我们还讨论了实时应用中使用的其他时空缺失数据插补方法。
对于大型城市网络,我们面临着数据并非无处不在的事实,尤其是在实时系统中,可能没有足够的时间来收集完整的数据。
一种简单的方法就是将缺失数据周围值的平均值填入。
[24] 通过“扩展贝叶斯网络”处理缺失数据。
他们利用交通网络中的因果关系,将缺失数据替换为其因果变量来构建网络。
这种方法的主要不足在于,一旦贝叶斯网络的结构和参数训练好,缺失数据的相对位置和时间也就固定了。 这通常是不真实的,因为数据可能会在不同的时间和地点丢失。
换句话说,一个模型只能处理一种缺失数据的情况。 如果我们面对的是一个真实的交通网络,我们不可能枚举每一个条件并为每一个条件训练一个模型。
“A bayesian network approach to traffific flflow forecasting,”
矩阵分解:
[25]通过矩阵分解的方法进行数据补全。交通数据被构建成一个矩阵,其中矩阵的每一个条目
表示点i和点j之间的交通速度。
基于非负矩阵三角分解框架,得到节点的潜在属性矩阵和属性交互矩阵。
“Latent space model for road networks to predict time-varying traffific,” KDD2016
[26]通过使用拉普拉斯矩阵最小化已知误差和约束,通过用因子矩阵重建数据矩阵来完成缺失数据的补全。 “Locality preserving projections,”
张量分解:
【28】使用张量分解分解来补全缺省的交通路网数据。他使用 CP 分解的加权优化版本来估算缺失的数据。
“Scalable tensor factorizations for incomplete data,”[29] 通过 Tucker 分解改进了这种方法。 即使数据缺失率非常高(高达 75%),他们也得到了相对准确的结果。 这些方法将数据组织为三向张量,具有日模式、小时模式和间隔模式。
“A tensor-based method for missing traffific data completion,”[ 30]【31】使用这种方法分析浮动汽车数据并获得更好的交通状态覆盖。 在这篇论文中,数据被组织为边连接模式、间隔模式和日模式的三向张量。
“Using tensor com pletion method to achieving better coverage of traffific state estimation from sparse flfloating car data,”“A new traffific prediction method based on dynamic tensor completion,”这些基于张量的方法有两个主要问题。
首先,他们一次只能处理一条道路或几条路段,这对于全市交通网络来说是不够的。
其次,他们没有定义选择张量分解秩的规则,但秩是张量分解最关键的参数之一。
2.2 multi-view learning
多视图学习方法涉及不同视图的多样性,可以基于各种特征子集子数据集进行优化。
[34] 提出了一种基于矩阵协同分解的方法 (MVL-IV),将不同的视图嵌入到共享子空间中,这样不完整的视图可以通过观察到的视图的信息来估计。
为了将不同的视图联系起来,MVL-IV假定不同的视图有不同的特征矩阵,但是不同的视图满足同一个系数矩阵
然而,它没有利用空间相关性并且可能会遇到数据不平衡问题,即如果视图之间存在大量缺失的数据,则系数矩阵 W 主要是从数据密集的视图中学习的。
解决多视图问题的另一种广泛使用的策略是张量分解[35]、[36],但这限制了需要每个视图的维数相同的常规张量。
此外,具有不完整视图的多核学习 [37]、[38] 只关注完成缺失的核而不是填充缺失值。
据我们所知,上述研究均未考虑空间和多视图问题。 因此,本文提出了一种有效的多视图城市统计数据缺失值插补模型。
3 问题定义和preliminary
3.1 问题定义
给定不完全的静态城市数据集,其中有n个不同的区域(r1,...rn),以及d个不同的视图(第p个视图的维度我们表示为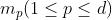 )。这篇论文旨在找到视图之间的关联性,以及精确地填充缺失信息。
)。这篇论文旨在找到视图之间的关联性,以及精确地填充缺失信息。
| 本文设计的符号 | 定义 |
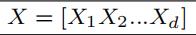 | 原始数据矩阵,包含 d 个视图 |
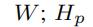 | 潜在空间矩阵,p 表示第 p 个视图 |
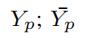 | 第 p 个视图的所有完整条目和缺失条目的指示矩阵 (0-1矩阵) |
| k;l | 潜在空间的维数; 和集群的数量 |
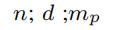 | 区域数量; 视图数量; 第 p 个视图中的属性维度 |
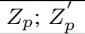 | 第p个视图中的加权矩阵 |
| L | 图拉普拉斯矩阵 |
| V | 集簇矩阵 |
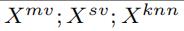 | 三个guidance matrix |
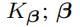 | 核矩阵; 核的系数 |
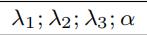 | 正则化参数 |
3.2 非负矩阵分解 Non-negative Matrix Factorization (NMF)
非负矩阵分解问题旨在将原始矩阵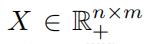 分解成两个矩阵
分解成两个矩阵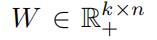 和
和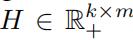 ,其中W和H代表了隐藏空间。
,其中W和H代表了隐藏空间。
在我们的问题里,W代表了区域之间的隐藏特征,H代表了数据视图之间的隐藏特征
这些矩阵中的每一列代表对应区域和统计字段的k个属性。
这些属性之间的相互作用决定了区域和统计字段之间的统计值。
于是,基于NMF的缺失值补全模型可以被描述成如下的优化目标:
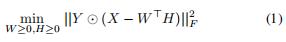
其中T是一个指示矩阵,当X(i,j)有观测数值的时候,Y是1,否则Y是0
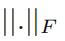 是Frobenius 范数
是Frobenius 范数
线性代数笔记:Frobenius 范数_UQI-LIUWJ的博客-CSDN博客
机器学习笔记:非负矩阵分解问题 NMF_UQI-LIUWJ的博客-CSDN博客
 是表示逐元素相乘的哈马德积
是表示逐元素相乘的哈马德积
3.3 多核K-means
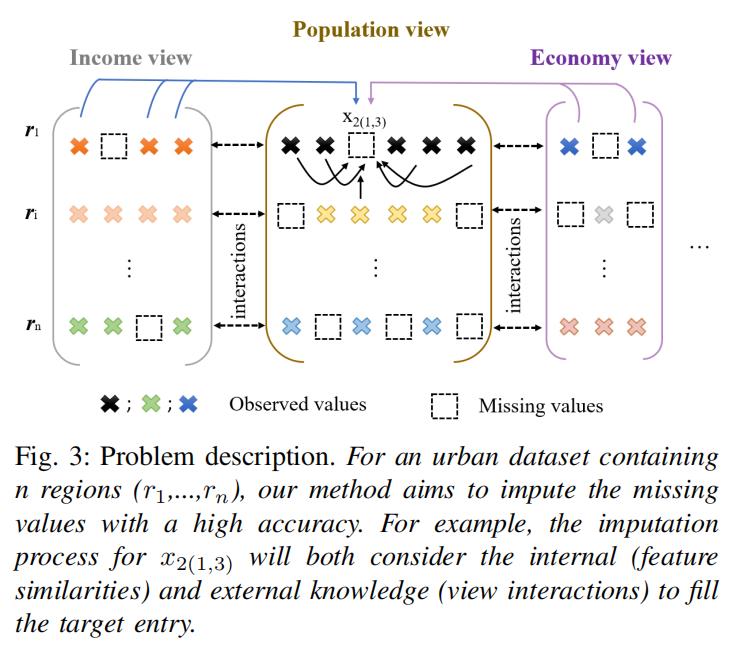
如图3所示,原始数据X有d个数据视图表示(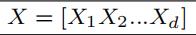 )
)
令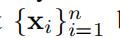 表示n个区域的样本集合。xi表示了第i个区域的统计学特征
表示n个区域的样本集合。xi表示了第i个区域的统计学特征
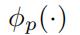 是将 x 映射到第 p 个再生希尔伯特核空间的 第 p 个视图映射。
是将 x 映射到第 p 个再生希尔伯特核空间的 第 p 个视图映射。
在这种情况下,每个样本都是由一组特征映射定义的多个特征表示
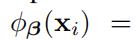
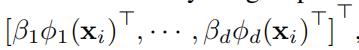
此时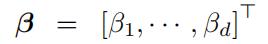 包含了d个核对应的系数,这些系数将在学习的过程中进行优化
包含了d个核对应的系数,这些系数将在学习的过程中进行优化
基于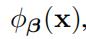 的定义,核函数可以被表示成
的定义,核函数可以被表示成
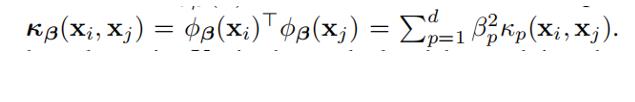
通过核函数,我们可以获得整个核矩阵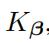 ,基于核矩阵,MKKM(multiple kernel K-means)的目标函数可以写成:
,基于核矩阵,MKKM(multiple kernel K-means)的目标函数可以写成:
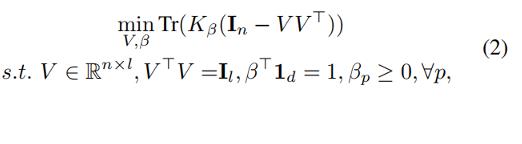
其中V是集簇矩阵,表示每个region在哪个集簇里面
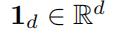 是全1的列矩阵
是全1的列矩阵
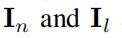 是单位矩阵
是单位矩阵
l是簇的数量
4 提出的模型(SMV-NMF)
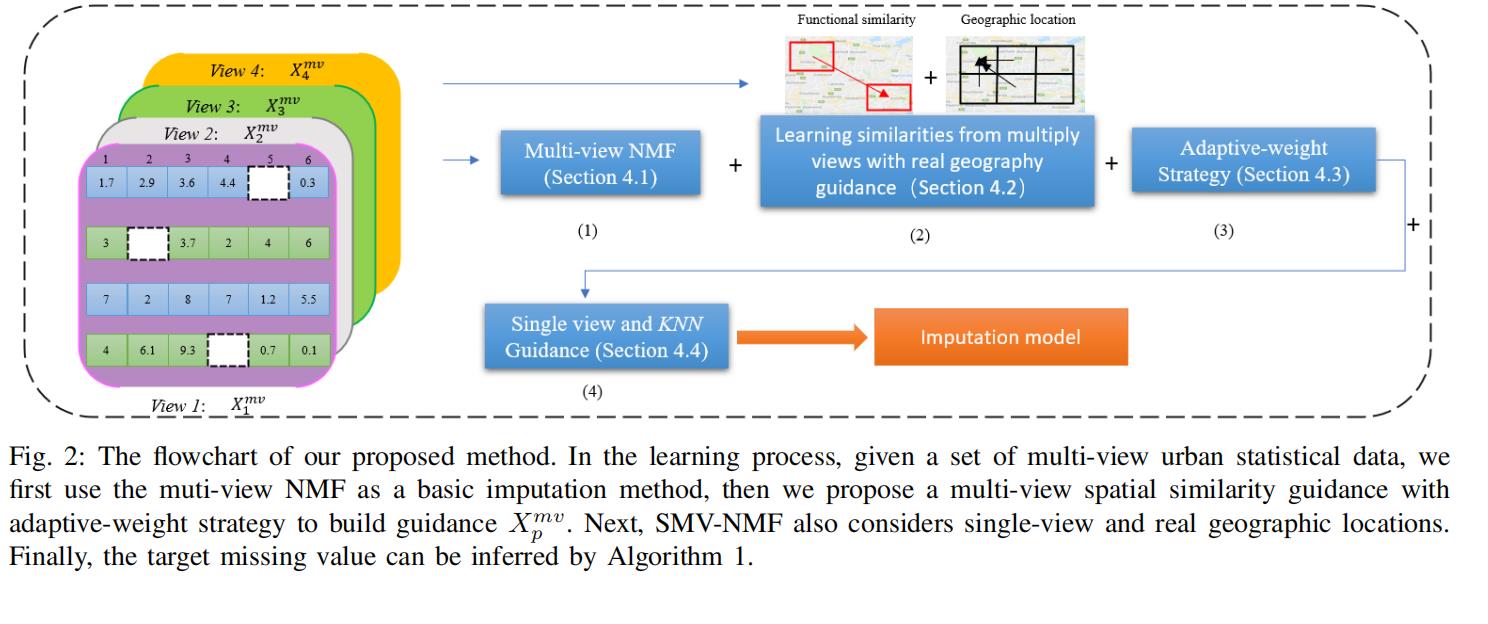
4.1 Multi-view NMF 多视图非负矩阵分解
在这个问题中,我们想学习一个不同region的潜在的子空间(这个不随p而改变,对于不同的视图,W是一样的)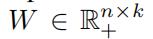 ,不同视图的矩阵
,不同视图的矩阵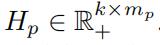 (一共有d个视图,即d个H矩阵)
(一共有d个视图,即d个H矩阵)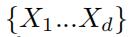
在这个情况下,Multi-view NMF的目标函数可以写成
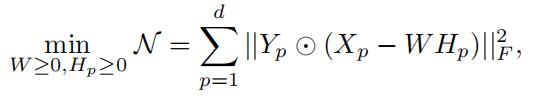
这里Yp是第p维视图的指示矩阵。当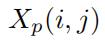 (第p个视图,第i个区域的第j个属性)有记录值的时候,
(第p个视图,第i个区域的第j个属性)有记录值的时候,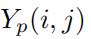 为1
为1
优化目标的意义是,对于每一个视图p,我都会有一个对应的各个点的属性特征
(n是点的数量,
是视图p中属性的数量)
对于所有视图,我们学习一个普适性的W,这个W在不同视图下看是一样的。
就是这个视图对应的“系数”矩阵
我们利用多视图 NMF 方法来查不同视图上各个region之间的潜在连接。
非负约束的优点之一是潜在特征的合理假设和结果的可解释性。 此外,由于城市统计数据的本身特点,缺失值必须是非负的,因此W和H应该被约束为非负字段。
4.2 多视图空间相似性指引
像2.2节所说的那样,基于多视图矩阵分解的方法没有利用空间相关性,可能会遇到数据不平衡问题 。
为了解决这个问题,我们对于第p个视图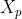 提出了相似指引(similarity guidance)
提出了相似指引(similarity guidance)
为了提取空间相关数据的不同视图之间的关联,我们设计了一种通过空间多核学习捕获区域相似性的方法,称为 S-MKKM。 其基本思路是城市的发展逐渐形成不同的功能群,如教育区、商圈等,属于同一群的区域之间会有很强的联系。
S-MKKM 利用多核 k 均值 (MKKM) 聚类算法(3.3)结合图拉普拉斯动力学策略(一种寻找空间结构相似性的有效平滑方法 )将区域聚类到不同的功能群。
详细地说,我们构建了一个图拉普拉斯矩阵L=D-M。其中D是度矩阵,M是图邻接矩阵,它是由区域物理空间的拓扑关系确立的(当且仅当区域i核区域j相邻的时候,
)
在3.3中,我们有MKKM的目标函数为:
在这里,引入图拉普拉斯矩阵后,S-MKKM模型的目标函数是
其中V是集簇矩阵,表示每个region在哪个集簇里面
α是正则化参数
为了获得完整的kernel,我们最初通过一种简单的方法(例如 KNN 或 MF,mean-filling)为每个视图估算缺失数据(不同初始化的效果在后文中会说明)。
因此,这个问题可以通过交替更新V(集簇矩阵)和β(核的系数)来解决[38]:
- 用固定的 β 优化 V。 在核系数β固定的情况下,V可以通过以下策略获得:
- 用固定的 V 优化 β。 在 V 固定的情况下,可以通过求解具有线性约束的二次规划来优化 β:
S-MKKM的目的是发现有相似特点的区域,并构建引导矩阵
当有了集簇矩阵V之后,我们就可以构建 了,构造过程如下:
了,构造过程如下:
1)对于不确定的条目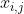 ,我们确定它对应的点
,我们确定它对应的点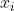 是第c个集簇,那么我们就用相应的
是第c个集簇,那么我们就用相应的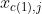 (也就是集簇中心点)的值来补全
(也就是集簇中心点)的值来补全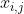
2)如果集簇中心点的值也不确定,一种贪心的策略会被使用,那就是找最近的已观测节点来进行补全
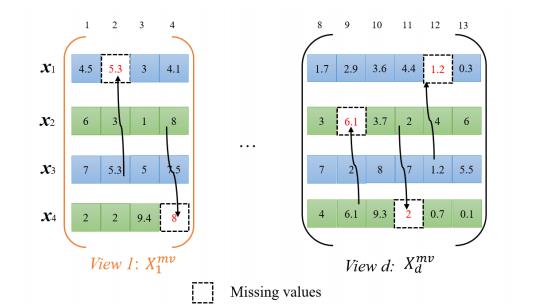
以上图为例,假如点1和点3是一类,点2和点4是一类。同时点2和点3是一个集簇。那么我们可以用集簇(点2、点3)对应位置有的值补全点1和点3缺失的值( 比如用x3,2填充x1,2、用x2,4填充x4,4、用x2,11填充x1,12)
如果中心位置没有值,那么我们先看同一集簇内附近的点有没有值,如果这一集簇内这个条目都没有的话,就看附近的不同集簇的点的这个值了(这里是用x4,9填充x2,9)
4.3 自适应权重NMF
对于补全的点,我们希望加上他们与集簇中心点的距离信息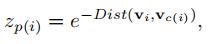
其中Dist表示 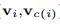 之间的欧几里得距离
之间的欧几里得距离
Zp相当于是补全的点的一个“惩罚项”
自适应权重NMF的优化目标函数可以写成:
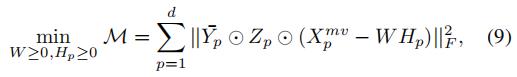
综合考虑NMF和这里的自适应权重NMF:
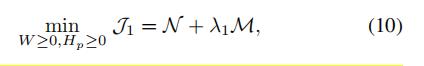
换句话说NMF可以看成是一个正则化项。
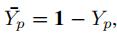 ,表示我们这里考虑的是之前没有值,也就是需要补全的那些值
,表示我们这里考虑的是之前没有值,也就是需要补全的那些值
4.4 单视图空间相似性指引 S-KKM
S-MKKM旨在同时考虑多个视图。然而,每个视图子集也有它独特的特征。不同区域在一个特定的视图下的关联,在补全问题中也是很重要的。
于是我们提出了单视图空间相似性指引,以及其相应的自适应权重NMF。
对于某一个特定的视图p,我们可以这么设计我们的单视图空间相似性指引
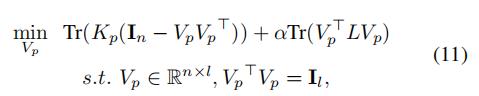
可以看出来,除了多了下标p,其他的和4.2S-MKKM没有什么区别
经过了这个,我们得到了我们单视图空间相似性指引矩阵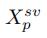
相应的自适应NMF的目标函数为
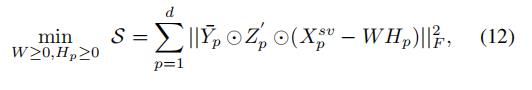
4.5 KNN相似性指引
对于每个区域的每一个视图,它的k近邻的信息也会对这个区域的属性有一定的增益作用
于是,我们也建立了KNN的相似性指引,以及它的自适应权重NMF
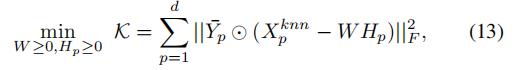
4.6 综合考虑各种自适应权重
综合考虑多视图、单视图和KNN的相似性执行对应的自适应权重矩阵,我们有:
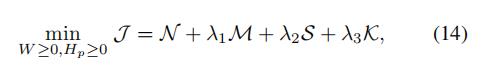
于是,我们最终的补全矩阵为:
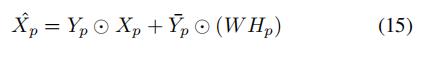
原来有值的就是原值,原来没值的就填上补全的值
4.7 之后两个小的章节是时间复杂度和训练过程,暂时略过
5 实验部分
5.1实验数据
我们找到了澳洲(ABS)和新西兰(NZS)的8个城市数据集。
在ABS中,每一个城市的数据集有四个视图(经济、家庭、收入、人口),四个视图分别有43、44、50、97个属性
不同试图的属性值我们限制在[0,10],这样我们就可以统一评估结果的正确与否。
5.2 Baseline
| sKNN | 使用空域上最近的k(在这里k取5)个邻居的平均值(单视图) |
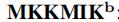 | 一个基于MKKM的方法 我们先学习MKKM,使得它可以分类不同的集簇。然后将它的k个”邻居“属性的平均值进行补全 |
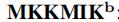 | 和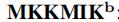 类似,不同的是,我们使用该集簇的平均值来进行补全 类似,不同的是,我们使用该集簇的平均值来进行补全 |
| NMF | 使用非负矩阵分解 |
| IDW | 一个在很多的工作中被拿来进行比较的全图空间学习 |
| UCF | 基于协同过滤的局部空间学习方法 |
| IDW+UCF | / |
|
MVL-IV
| 一种先进的基于矩阵协因子分解的多视图学习方法,它学习同一个系数矩阵来连接多个视图 |
|
ST-MVL
| 计算时空缺失数据的最新方法。由于时间信息缺失的问题,我们只使用它的空间部分。 |
| SMV-MF | 我们的模型去掉非负矩阵分解,换成矩阵分解 |
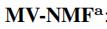 | 去除拉普拉斯矩阵限制
|
 | 去除KNN相似性指引
|
5.3 衡量标准

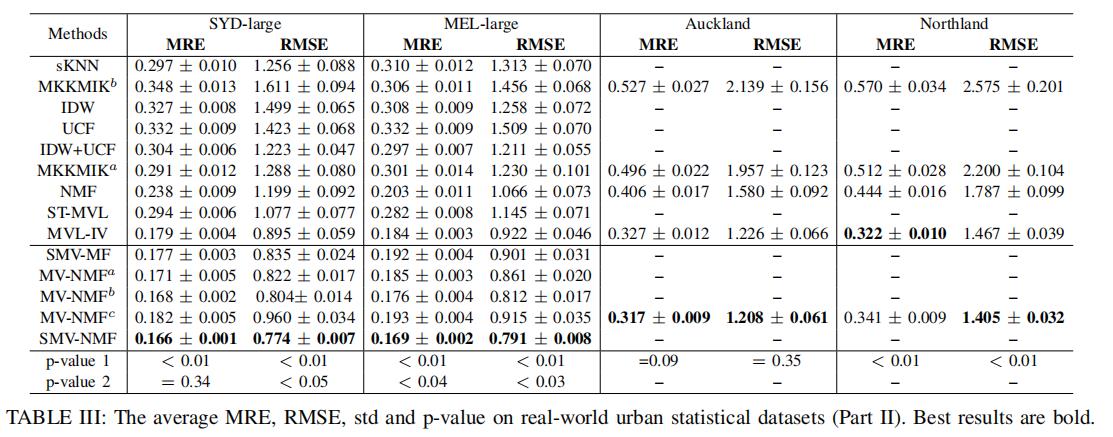
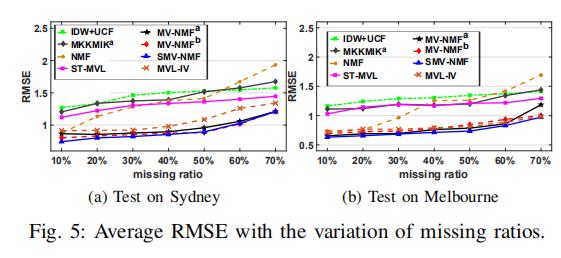
5.4 实验结果
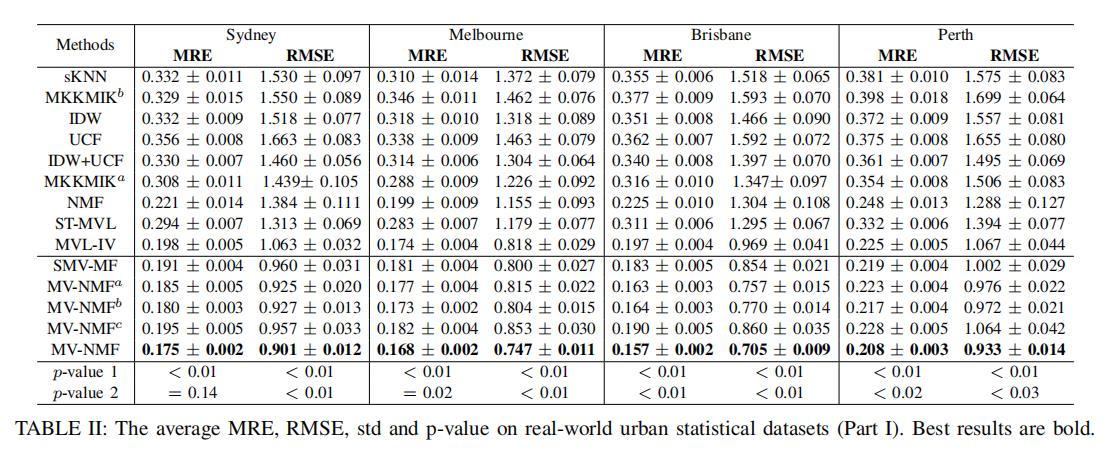
很明显地发现,我们提出来的模型(及其变体),达到了最好的效果。
MVL-IV相比于ST-MVL和MKKMIK来说,效果好很过,很为MVL-IV考虑了多视图问题
相比于MVL-IL,本模型的优点在于它学习隐藏空间中点与点之间的相似度,而不是原始数据点与点的相似度。其次,本模型融入了先验知识(自适应权重)来补全每一个丢失的信息。这些都对于空间信息补全有着很大的作用。
尽管ST-MVL在时空丢失信息补全的问题中有着很高的效果,但是对于本问题,当时间信息没有的时候,仅仅依靠空间信息,ST-MVL并不能达到很好的效果
同时,我们也发现,我们模型中,注入非负矩阵分解的非负限制、图拉普拉斯矩阵的限制、KNN的限制等,有尤其作用所在。
信息丢失率和预测准确度之间的关系
这两个模型对于丢失率很敏感(个人感觉是,因为这两个都完全没有考虑空域的属性,比如拉普拉斯矩阵,所以一旦丢失率高,对于整体的空间属性模型就所知甚少了)
5.5 模型的泛化性
模型使用墨尔本和布里斯班的数据作为测试集,悉尼的数据作为验证集,澳洲的其他数据作为训练集,以测评模型的泛化性。
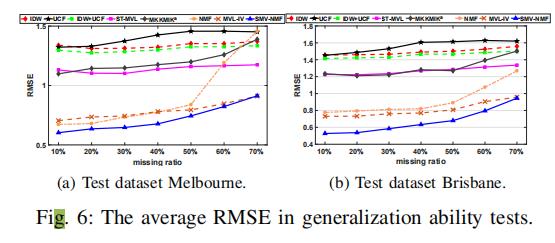
实验表明,本模型具有很强的泛化能力,可以把构建好的模型从一个城市的数据集迁移到另一个城市。这是因为城市之间有很强的相似性和关联性。(比如城市中不同功能的区域数量大致相同。这就导致了集簇的数量差不多)
5.6 不同view 的权重
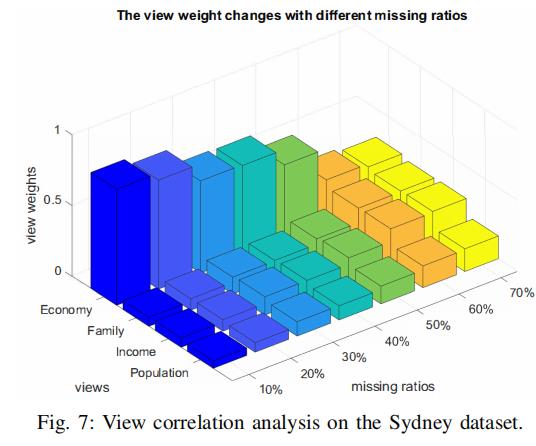
可以看到,当missing rate小的时候,经济(economy)占据了很高的优先级;当missing rate大的时候,几个因素就需要综合考虑了
个人推测是前面MKKM中
的那些β的占比
以上是关于论文笔记:Missing Value Imputation for Multi-view UrbanStatistical Data via Spatial Correlation Learning的主要内容,如果未能解决你的问题,请参考以下文章