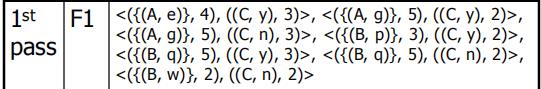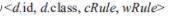论文笔记：Integrating Classification and Association Rule Mining （即，CBA算法介绍）

Posted 2021-10-02 UQI-LIUWJ

1998 KDD

0 摘要

        分类规则挖掘旨在发现数据库中的一小组规则，形成一个准确的分类器。 关联规则挖掘发现数据库中存在的所有满足最小支持度和最小置信度约束的规则。 对于关联规则挖掘，发现的目标不是预先确定的，而对于分类规则挖掘，则只有一个预先确定的目标。

        在本文中，我们建议整合这两种挖掘技术。 集成是通过专注于挖掘关联规则的特殊子集来完成的，称为类关联规则 (CAR)。 还给出了一种基于发现的 CAR 集构建分类器的有效算法。

         实验结果表明，以这种方式构建的分类器通常比最先进的分类系统 C4.5 产生的分类器更准确。 此外，这种集成有助于解决当前分类系统中存在的许多问题。

1 introduction

        集成是通过关注一个特殊的关联规则子集来完成的，该子集的右侧仅限于分类类属性。 我们将此规则子集称为类关联规则 (CAR)。

        现有的关联规则挖掘算法（Agrawal 和 Srikant 1994）适用于挖掘满足最小支持度和最小置信度约束的所有 CAR。

        关联规则（Association Rules）笔记_UQI-LIUWJ的博客-CSDN博客

        这种适应是必要的，主要有两个原因：

        1）在关联规则（Apriori算法中），并没有很多的关联（associations）。但是在分类问题中，我们有很多的关联数据。如果不使用CAR的话，挖掘所有的关联规则，会导致计算量爆炸。

        2）分类数据集通常包含许多连续（或数字）属性。 挖掘具有连续属性的关联规则仍然是一个主要的研究问题。 我们的适应涉及基于分类预定类目标离散化连续属性。 为此，有许多很好的离散化算法可以使用

我们提出的CAR数据挖掘包括了三步：

1）离散化连续的属性（如果需要的话）

2）生成所有的类关联规则

3）基于CAR，建立一个分类器

2 问题定义

        我们提出的框架假设数据集是一个正常的关系表，它由 l 个不同的属性描述的 N 个案例组成。 这 N 个案例已被分类为 q 个已知类别。 属性可以是分类（或离散）或连续（或数字）属性。

        在这项工作中，我们统一对待所有属性。 对于分类属性，所有可能的值都映射到一组连续的正整数。 对于连续属性，其取值范围被离散化为区间，区间也映射为连续的正整数。

        通过这些映射，我们可以将数据案例视为一组（属性、整数-值）对和一个类标签。 我们称每个（属性，整数值）对为一个项目item。 

       

        令D是数据集，I是数据集里面所有的条目，Y是类标签的集合。

        当时，我们称一个一个数据案例d∈D 包含 条目的一个子集

       

         一个类关联规则（CAR）是一个如下格式的关联规则，其中

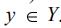
       如果在D中包含 X的数据案例中，c%的案例被标记为类别y，那么我们称 D中的规则X->y有着c的置信度（confidence）。

        如果在D中，s%的案例包含X，同时被标记为类别y，那么那么我们称 D中的规则X->y有着s的支持度（support）。

        我们的目标是：

（1）生成CAR的完整集合，这个集合满足最小支持度（minsup）以及最小置信度（minconf）

（2）建立一个基于CAR的分类器

        

 3 模型整体框架

        整体的算法被称为CBA算法(Classification Based on Associations)。它包含了两个部分：一个规则生成器（CBA-RG），这个基于Apriori 算法，来发掘关联规则；一个分类器（CBA-CB）

3.1 CBA-RG的基本概念

        CBA-RG的基本操作是找到所有超过最小支持度的规则项（ruleitem）。

        一个规则项是一个如下的结构<condset,y>，其中condset是一个items集合，y∈Y是一个类别标签。

        condset的支持度计数（support count）是D中包含condset的数量。【记作condsupCount】

        规则项的支持度计数（是D中包含condset，同时是被标记为y的数量。【记作rulesupCount】

        规则项的支持度是

        规则项的置信度是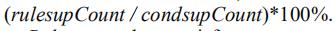

满足最小支持度的规则项被称为频繁规则项（frequent ruleitem）；否则则是不平凡规则项。

 举个例子，对于如下的规则项：

（表示属性A为1，属性B为1的时候，类别是1）

        如果condset的支持度计数是3，规则项的支持度计数是2，|D|=10.

        那么规则项的支持度是20%，置信度是67%

        对于有着相同condset的规则项，有着最高置信度的规则项被选择为可能规则（possible rule,PR)，我们就用这个代表ruleitems

         如果不止一个ruleitem有着相同的最高置信度，那么我们随机选择一个ruleitem作为PR

        满足最小置信的规则，我们称之为精准

        最终的CAR会包含所有又频繁又精准的PR

3.2 CBA-RG算法

        CBA-RG 算法通过对数据进行多次传递来生成所有频繁规则项。

        在第一遍中，它计算单个规则项的支持度并确定它是否是频繁的。

        在随后的每一次传递中，它都从在前一次传递中发现频繁的规则项的种子集开始。

         它使用这个种子集来生成新的可能频繁出现的规则项，称为候选规则项。 这些候选规则项的实际支持度是在数据传递期间计算的。

        在传递结束时，它确定哪些候选规则项实际上是频繁的。 从这组频繁规则项中，它生成规则 (CAR)。

        【有点类似于Aprori】

        令k-ruleitem表示一个ruleitem，其中它的condset有k个条目

        令Fk表示频繁k-ruleitem的集合。其中的每个元素又是如下的格式：

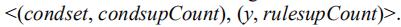
        令Ck是候选k-ruleitems的集合

        于是CBA-RG的算法如下：

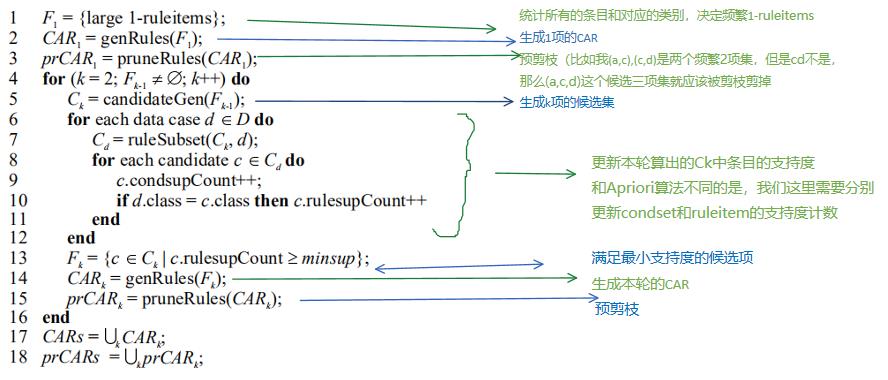
3.2.1 举例说明（非论文内容）

 源数据集：

第一步：选取所有的1-ruleitems，然后把支持度小于minsup的去掉

这里枚举所有的属性+l类别对，然后一一筛选

 表示 属性A为e的一共有4个，然后属性A为e的情况下，类别C为y的一共有3个

上面的这些时已经把支持度小的去掉了（比如<({(A,e)},4),((C,n),1)>

第二步

先找所有的候选集，（将两个分到的类一样的k-1 ruleitems 合并）

 然后对于这些候选集，计算他们的支持度，挑选出比最小支持度大的那些项集

最后

合并第一pass和第二pass得到的频繁项集

 

3.3.2 剪枝CAR举例：

去掉那些置信度比最小置信度还小的项集

 3.3 CBA-CB

        本节介绍使用 CAR（或 prCAR）构建分类器的 CBA-CB 算法。 要从整个规则集中生成最佳分类器，将涉及在训练数据上评估其所有可能的子集，并选择具有正确规则序列的子集，该子集给出的错误数最少。 有2^m这样的子集，其中m是规则的数量，可以超过10,000，更不用说不同的规则序列了。

         这显然是不可行的。 我们提出的算法是一种启发式算法。 但是，与 C4.5 构建的分类器相比，它构建的分类器性能非常好。 在介绍算法之前，让我们定义生成规则的排序规则。 这用于为我们的分类器选择规则。

        给定两个规则，的条件是：

        1）ri的置信度大于rj的置信度

        2）如果置信度一样的话，ri的支持度大于rj的支持度

        3）如果都一样的话，ri比rj先生成出来

        令R是一套生成的规则（剪枝过的或者没有剪枝的），D是训练数据。算法的基本思想是在R中选择一组高优先级规则来覆盖D。 分类器的格式如下：

         

        

        在对未见案例进行分类时，满足该案例的第一个规则将对其进行分类。 如果没有适用于这种情况的规则，它将采用默认类。 用于构建此类分类器的算法（称为 M1）的原始版本包含三个步骤：  【M1适合小的数据集】

 

        该算法满足两个主要条件：

        条件 1. 每个训练案例都被覆盖该案例的规则中具有最高优先级的规则覆盖。 这是因为在第 1 行中完成了排序。

        条件 2. C 中的每条规则在选择时都正确分类了至少一个剩余的训练案例。 这是由于第 5-7 行

         这种算法很简单，但效率低下，尤其是当数据库不常驻主存时，因为它需要多次遍历数据库。  

举例说明： （源论文没有）

 1 先排序 rule的顺序是 5 1 3 6 2 4

 2 按照rule的顺序，进行CBA，维护一个这样的表格

当前考虑规则号	当前规则涉及的rule_item （即 temp）	这些rule_item里面分类正确的数量	这些rule_item里面分类错误的数量	剩余item的默认分类（取多的那个）	在当前分类方式下，总的错误数	剩余未考虑的rule_item
5	(7) (8)	2	0	y	3【(6) (9)(10)错误】	(1)(2)(3)(4)(5)(6)(9)(10)
1	(1)(2)(3)(9)	3	1 【(9)错误】	y	3【(6)(9)(10)错误】	(4)(5)(6)(10)
				n	3 【(4)(5)(9)错误】	(4)(5)(6)(10)
				上面无论默认值是y还是n，总错误数量都是一样的，所以随机选择一个，作为default_class
3	/	/	/	/	/	(4)(5)(6)(10)
6	(4)(5)(6)	2	1 【(6)错误】	n	2 【(6)(9)错误】	(10）
2	/	/	/	/	/	(10）
4	(10)	0	1 【10错误】	/	3 【(6)(9)(10)错误】	/

 我们最小的错误数是在考虑(6)的时候，所以最终的分类器由规则(5)(1)(6)组成

        下面，我们展示了算法的改进版本（称为 M2），其中只对 D 进行了略多于一次的传递。关键点是，不是对每个规则的剩余数据（在 M1 中）进行一次传递，我们 现在在 R 中找到覆盖每种情况的最佳规则。 M2由三个阶段组成 【M2适合大的数据集】

阶段1：      

   对于D中的每一个条目d，我们找到正确分类d的最高优先级的规则cRule和错误分类d的最高优先级的规则wRule。

        如果那么条目d将是由cRule覆盖。

        如果 那么可能就会更复杂一点，因为我们不知道wRule和cRule中间的那一个会最终覆盖d 

        为了决定这个，对于每一个的d，我们维护一个数据结构： <dID, y, cRule, wRule>  。其中dID是d的id，y是d的类别。

        令A表示<dID, y, cRule, wRule>  的集合

        U是所有cRules的集合

        Q是所有满足的cRules的集合

 举例

还是这个例子

与M1不同的是，我们需要不需要按照rule遍历，而是按照rule_item遍历。

 1 先排序 rule的顺序是 5 1 3 6 2 4

2 然后也维护一张表

当前rule_item (A,B,C)	可以分类当前rule_item的规则（按照从大到小的顺序）	正确分类当前rule_item的、拥有最高优先级的规则cRule	错误分类当前rule_item的、拥有最高优先级的规则wRule	U，所有cRules的集合	Q, 满足的cRules的集合	A，不满足的部分组成的信息
(e,p,y) 1	1，3	1	/	1	1	/
(e,p,y) 2	1，3	1	/	1	1	/
(e,q,y) 3	1，4	1	/	1	1	/
(g,q,y) 4	6，2，4	6	2	1，6	1，6	/
(g,q,y) 5	6，2，4	6	2	1，6	1，6	/
(g,q,n) 6	6，2，4	2	6	1，6，2	1，6	(6,n,2,6)
(g,w,n) 7	5，2	5	/	1，6，2，5	1，6，5	(6,n,2,6)
(g,w,n) 8	5，2	5	/	1，6，2，5	1，6，5	(6,n,2,6)
(e,p,n) 9	1，3	/	1	1，6，2，5	1，6，5	(6,n,2,6)， (9,n,null,1)
(f,q,n) 10	4	/	4	1，6，2，5	1，6，5	(6,n,2,6)， (9,n,null,1)， (10,n,null,4)

 步骤2

举例（接着stage1）

A中有：(6,n,2,6)，(9,n,null,1)，(10,n,null,4)

U中有：1，6，2，5 

首先看(6,n,2,6)：【(g,q,n)】

         wRule = 6 is marked 

                A. 2.classCasesCovered[n] -- = 0

                B. 6.classCasesCovered[n] ++ = 1

        （相当于使用wRule代替cRule 分类rule_item(6)）

然后看(9,n,null,1)：【(e,p,n)】

        wRule = 1 is marked

                A. 1.classCasesCovered[n] ++ = 1

                （相当于原本没有规则可以覆盖rule_item(9)，现在用规则覆盖之）

最后看(10,n,null,4)：【(f,q,n)】

         wRule = 4 is not marked

        wSet = {1,6,2,5}  （所有错误分类rule_item(10)，且优先级比NULL大的U中的规则） 

        这几个的.replace() 为<Null,10,n>     

返回的Q为1,6,5,4

 举例：（接着stage 2）

Classes: 5 Y + 5 N

ruleErrors = 0

Q = 5,1,6,4 （排序）

首先看规则5：

        不进入循环

        ruleErrors=0

        此时的classDistr 为 5Y+3N （5已经成功分类了两个n【7，8】）

        defaultClass=Y

        defaultError=3

        totalErrors=3

        C=<5,Y,3>

然后看规则1：

         不进入循环

        ruleErrors = 1

        classDistr = 2 Y + 2 N （1成功分类三个Y 【1，2，3】，错误一个【9】）

        defaultClass=N or Y

        defaultErrors=2

        totalErrirs=4

        C=<5,Y,3>,<1,N,3>

然后是规则6：

        不进入循环

        ruleErrors=2 (规则1的一个+规则6的一个）

        classDistr=N

        defaultClass=N

        defaultError=0

        totalErrors=2

        C=<5,Y,3>,<1,N,3>,<6,N,2>

最后是规则4：

        不进入循环

        ruleErrors=3（规则1的一个，规则6的一个，规则4的一个）

        /

        totalErrors=3

        C=<5,Y,3>,<1,N,3>,<6,N,2>,<4,/,3>

所以最后的是<5,Y,3>,<1,N,3>,<6,N,2>，和M1的一样

 4 实验部分

 在实验中，最小置信度被设置为50%

而对于最小支持度，这是一个很复杂的设定，最小支持度对于分类器的质量有着很强的作用。如果最小支持度被设置的很高，那么有些可取的挥着因为没有达到最小支持度的限制而被丢弃，这会导致CAR效果不佳。在我们的实验中，我们设置最小支持度为1%

与此同时，我们也设定了总候选规则的数量上限，80000。但是，在后面我们进行实验的26个数据集中，16个无法在80000的限制内完成，这说明分类数据通常有着很大数量的关联

 

 我们说一下表格某几列的含义：

第二列：它显示了使用原始数据集（即没有离散化）进行的十次完整的 10 倍交叉验证中 C4.5rules 的平均错误率。 我们没有展示 C4.5 树的详细结果，因为它在 26 个数据集上的平均错误率更高

第三列：它显示了离散化后 C4.5 规则的平均错误率。 此处不使用 C4.5 树的错误率，因为其平均错误率较高。

第四列：它给出了使用我们的算法构建的分类器的平均错误率，在十次交叉验证中 minsup = 1%，同时使用 CAR 和不频繁规则（满足 minconf 的，但是因为不满足最小支持度而被丢弃的规则）。 我们使用不频繁的规则是因为我们想看看它们是否影响分类精度。 第一个值是使用规则生成时未剪枝的规则构建的分类器的错误率，第二个值是规则生成时使用未剪枝的规则构建的分类器的错误率。

 第五列：它显示了在我们的分类器构建中仅使用 CAR 的错误率，在规则生成中没有或有剪枝（即 prCAR）。

        从这 26 个数据集中可以清楚地看出，CBA 产生了更准确的分类器。 平均而言，错误率从 C4.5 规则（无离散化）的 16.7% 降低到 CBA 的 15.6-15.8%。 此外，我们的系统在 26 个数据集中的 16 个数据集上优于 C4.5 规则。 我们还观察到，在没有或有剪枝的情况下，最终分类器的准确性几乎相同。 因此，那些 prCAR（剪枝后）足以构建准确的分类器。 请注意，与离散化后的 C4.5 规则的错误率 (17.1) 相比，CBA 更加优越。

第六列：它给出了每次交叉验证中由算法 CBA-RG 生成的规则的平均数量。 第一个值是 CAR 的数量。 第二个值是 prCAR 的数量（修剪后）。 我们看到修剪后剩下的规则数量要少得多。

第七列：它给出了在每次交叉验证中生成规则所需的平均时间。 第一个值是不进行修剪时所用的时间。 第二个值是使用修剪时所用的时间。 通过修剪，算法 CBA-RG 的运行速度只会稍微慢一些。

第八列：它显示了仅使用 prCAR 构建每个分类器所需的平均时间。 第一个值是方法1（M1）的运行时间，第二个值是方法2（M2）的运行时间。 我们看到 M2 比 M1 更有效率。

第九列：它给出了 CBA-CB 使用 prCAR 构建的分类器中规则的平均数量。 我们的分类器中的规则通常比 C4.5 生成的规则多（此处未显示）。 但这不是问题，因为这些规则仅用于对未来案例进行分类。 可以在 CAR（或 prCAR）中找到易于理解和有用的规则。 这些规则可能会或可能不会由 C4.5 生成，因为 C4.5 不会生成所有规则。

下面，我们总结了另外两个重要的结果。 ·

        虽然我们无法使用 80,000 的限制在 26 个数据集中的 16 个中找到所有规则，但使用发现的规则构建的分类器已经非常准确。 事实上，当 26 个数据集中的限制达到 60,000 时（我们已经尝试了许多不同的限制），生成的分类器的准确性开始稳定。 继续进行只会生成具有许多难以理解和难以使用的条件的规则。 ·

         我们还使用磁盘而不是主内存中的数据集运行CBA算法，并将所有数据集的案例数增加了32倍（最大数据集达到160,000个案例）。