《STTR：Revisiting Stereo Depth Estimation From a Sequence-to-Sequence Perspective with Transformers》(
Posted m_buddy
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《STTR：Revisiting Stereo Depth Estimation From a Sequence-to-Sequence Perspective with Transformers》(相关的知识，希望对你有一定的参考价值。
参考代码：stereo-transformer
1. 概述
导读：这篇文章通过transformer机制实现了一种立体匹配算法（STTR），在该方法中将立体匹配问题转换为序列上的响应问题，使用未知信息编码与注意力机制替换了传统匹配方法中的cost volume策略。由于替换了cost volume解除了预定max-disparity假设的限制，增强了网络的泛化表达能力。在估计视差图的同时显示地估计遮挡区域的概率结果。此外，为了寻找右视图到左视图的最佳匹配，文中对其中的匹配矩阵添加熵约束，从而实现对匹配过程的添加唯一性约束。
将文章的方法（STTR）与correlation-based和3D convolution-based方法进行比较，可以归纳为：
- 1）STTR与correlation-based方法比较：STTR在进行左右视图匹配的时候通过self-attention和cross-attention建立相关性，并且对像素点匹配的结果进行唯一性约束；
- 2）STTR与3D convolution-based方法比较：STTR通过attention建立像素之间的关联，而不是通过设定max-disparity的形式建立cost volume；
文章的方法在下面几个数据集下的结果：
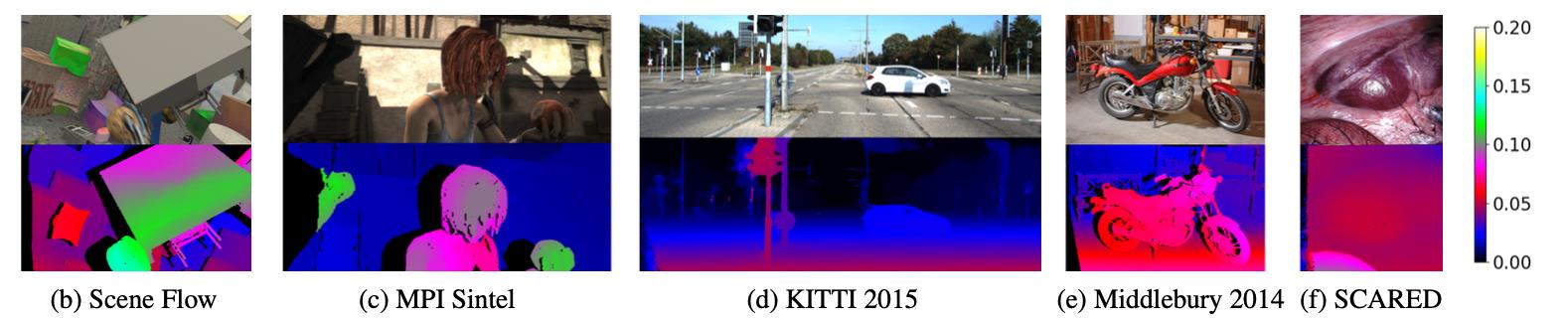
2. 方法设计
2.1 pipline
文章提出的方法pipeline见下图所示：
在上图中可以看到左右两视图经过一个共享backbone和tokenizer进行特征抽取，这部分的实现可以参考：
# backbone 部分
# module/feat_extractor_backbone.py#L15
class SppBackbone(nn.Module):
…
# tokenizer部分
# module/feat_extractor_tokenizer.py#L62
class Tokenizer(nn.Module):
…
经过上面两个过程对特征进行抽取得到的是channel为 C e C_e Ce，空间分辨率与原输入尺度 ( I h , I w ) (I_h,I_w) (Ih,Iw)一致的特征图。之后这些特征图便与位置编码组合经过 N N N层的attention操作预测得到粗预测结果，之后再改结果的基础上进行refine得到最后的结果。
2.2 Transformer操作
文章提出的transformer结构可见下图：
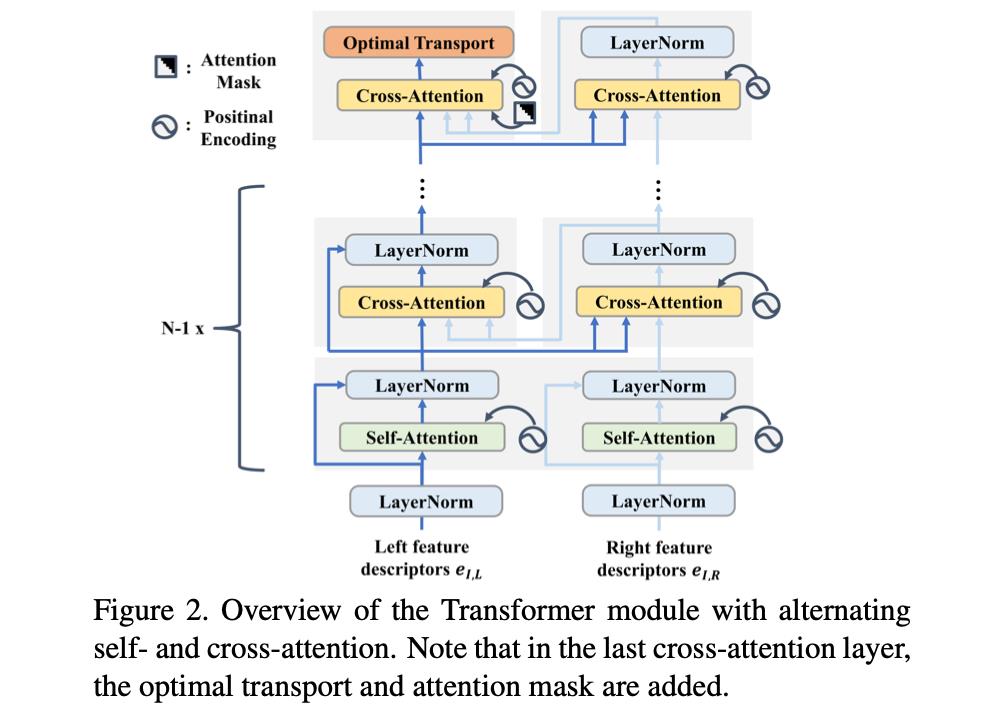
在上图中可以看到其中首先会经过几个attention层（带position encoding），之后
特征经过带mask的cross-attention得到最后优化的特征。
2.2.1 attention操作
这里采用的attention操作是multi-head attention，可以参考pytorch的实现nn.MultiheadAttention。这里会将特征图在channel维度进行分组操作，对不同的分组进行运算从而增强特征的表达的能力，对于组的划分可以描述为：
C
h
=
C
e
N
h
C_h=\\frac{C_e}{N_h}
Ch=NhCe，其中分母是划分的组的数量。在每个分组中会产生回应的query、key和value向量，其分别表示为：
Q
h
=
W
Q
h
e
I
+
b
Q
h
Q_h=W_{Q_h}e_I+b_{Q_h}
Qh=WQheI+bQh
K
h
=
W
K
h
e
I
+
b
K
h
K_h=W_{K_h}e_I+b_{K_h}
Kh=WKheI+bKh
V
h
=
W
V
h
e
I
+
b
V
h
V_h=W_{V_h}e_I+b_{V_h}
Vh=WVheI+bVh
有了计算权重的所需的变量之后，结下来就是计算加权组合因子了：
α
h
=
s
o
f
t
m
a
x
(
Q
h
T
K
h
C
h
)
\\alpha_h=softmax(\\frac{Q_h^TK_h}{\\sqrt{C_h}})
αh=softmax(ChQhTKh)
接下来就是对之前划分出来的组进行组合：
V
o
=
W
o
C
o
n
c
a
t
(
α
1
V
1
,
…
,
α
h
V
h
)
+
b
o
V_o=W_oConcat(\\alpha_1V_1,\\dots,\\alpha_hV_h)+b_o
Vo=WoConcat(α1V1,…,αhVh)+bo
最后与原特征进行相加得到增强之后的特征：
e
I
=
e
I
+
V
o
e_I=e_I+V_o
eI=eI+Vo
在文中计算上述attention是采用两种方式：
- 1）self-attention：在该计算过程中所有attention操作所需的 Q h , K h , V h Q_h,K_h,V_h Qh,Kh,Vh都是来自于同一视图产生的特征，这部分可以参考：
# module/transformer.py#L116
class TransformerSelfAttnLayer(nn.Module):
…
- 2）cross-attention：在这个操作中 Q h Q_h Qh是来自于source图像产生的特征，而 K h , V h K_h,V_h Kh,Vh是来自于target图像产生的特征。需要注意的是这里的source和target是相对的，相当于在计算cross-attention的过程中是会进行交换的，实现双向计算。其实现可以参考：
# module/transformer.py#L150
class TransformerCrossAttnLayer(nn.Module):
…
2.2.2 position encoding
在上面的多层attention过程中描述了像素与像素之间的关系，但是对于那些弱纹理甚至是无纹理区域的处理就变得比较困难了。对此文章为这些点通过建立相邻点（特别是那些诸如边缘点的显著性特征）的联系，优化对于弱纹理区域的适应能力，因而这里就使用到了用于相对位置建模的position encoding，其实现可以参考：
# module/pos_encoder.py#L13
class PositionEncodingSine1DRelative(nn.Module):
…
则上一节中讲到的attention权重经过position encoding的重新编码可以得到下面的权值组合形式：
对于这部分的实现可以参考：
# module/attention.py#L20
2.2.3 attention mask
在经过多层attention操作之后，已经可以构架出左视图和右视图上每个像素的对应关系了，但为了排除一些无关干扰，文章通过建立下三角mask的形式去约束对应点的位置，这部分的计算描述为：
# module/transformer.py#L213
def _generate_square_subsequent_mask(self, sz: int):
…
2.2.4 Optimal Transport
在进行特征匹配的时候为了右视图中的像素能被对应到左视图中最匹配的像素，文章对匹配矩阵
T
\\mathcal{T}
T添加了约束，也就是上文中提到的唯一性约束。其是在匹配矩阵的基础上添加熵正则化，可以描述为：
T
=
arg min
T
∈
R
+
I
w
∗
I
h
∑
i
,
j
=
1
I
w
,
I
h
T
i
j
M
i
j
−
γ
E
(
T
)
\\mathcal{T}=\\argmin_{\\mathcal{T}\\in R_{+}^{I_w*I_h}}\\sum_{i,j=1}^{I_w,I_h}\\mathcal{T}_{ij}M_{ij}-\\gamma E(\\mathcal{T})
T=T∈R+Iw∗Ihargmini,j=1∑Iw,IhTijMij−γE(T)
s
.
t
.
T
1
I
w
=
a
,
T
1
I
h
=
b
s.t.\\ \\mathcal{T}1I_w=a,\\mathcal{T}1I_h=b
s.t. T1I
双目深度算法——基于Transformer的方法（STTR）
双目深度算法——基于Transformer的方法（STTR）
IMPROVING ADVERSARIAL ROBUSTNESS REQUIRES REVISITING MISCLASSIFIED EXAMPLES
《Revisiting Self-Supervised Monocular Depth Estimation》论文笔记
论文阅读 | Revisiting Joint Modeling of Cross-document Entity and Event Coreference Resolution