双频移相线

Posted 2021-10-02 硬件老钢丝

这里的双频移相线主要用于Doherty功率放大器的相位补偿。
参考论文：2012 Design Methodology for Dual-Band Doherty Power Amplifier With Performance Enhancement Using Dual-Band Offset Lines

我们主要介绍双频移相线。

一、基本结构

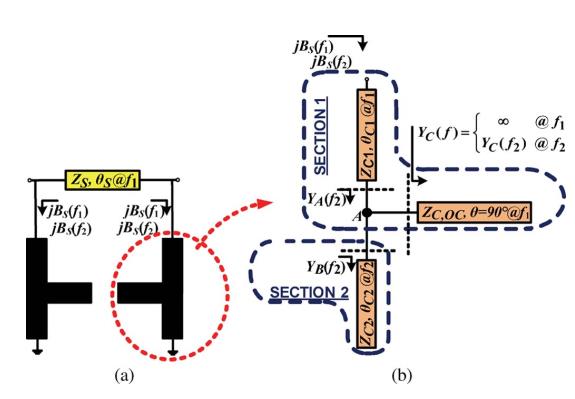
结构本质上是一个PI型结构，两条分支采用一种新的结构，第一部分是为了先对频率f1进行一个设计，然后再对f2进行处理，这样就可以保证在处理f2的时候，不会受到f1的干扰。

二、公式构成

双频移相线：两个频率处的电长度是不一样，这个取决于我们的设计，特性阻抗都是50欧姆。
首先是PI型结构的S参数：公式（1）

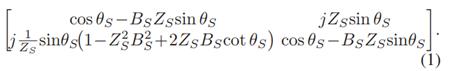
根据这个S参数，我们可以得到

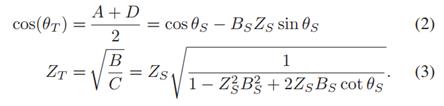
将公式（3）重新排列，其中n为f1和f2的比值。ZT为两个频率处的特性阻抗。

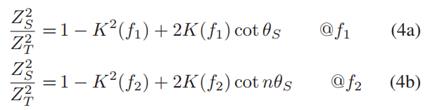
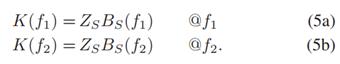
同样的，公式（2）也可以展开：

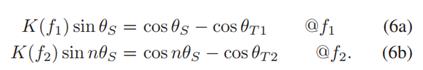
把公式（6）代入公式（4），可以得到对应的两个频率处的Zs

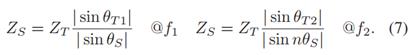
通过公式（7）

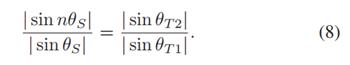
对于公式（8），通常我们是不太好去求解的，文章提供了一个附录，但是考虑到计算不好计算，我们直接用Mathematcia编写公式进行计算。
在计算出Theta_s以后呢，我们就可以利用下下述公式，进行Zs的求解了。
为了增加设计的灵活性，我们枝节的三个阻抗都可以灵活地去取值，Zc1,Zc2,Zoc 一般可以都取成50欧姆

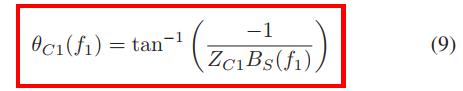
根据这个，可以求出theta_f1的长度

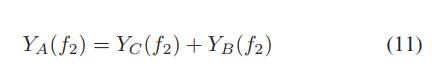
theta_oc =90度，为了实现在f1处的短路。

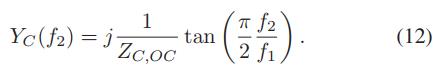
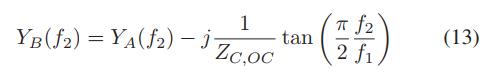
三、编程求解验证

首先，论文中给定的两个相位值：theta_T1=55.84° theta_T2=159.68°
为了验证我们的结论可靠性，我们需要用公式进行验证，也方便我们之后进行应用。

首先是theta_s的求解，考虑到计算的复杂性，这里利用mathematica软件进行计算：
程序：NSolve[0.4196Sin[x] == Sin[3500x/1960] && 0 < x < 10, x, Reals]

这里的0.4196是公式（8）右端的计算结果值。

通过求解我们选用比较短的线长，也就是theta_s=1.51718*180/pi=86.93°

下面就用MATLAB软件进行计算。
clear
clc
theta_s=input(‘请输入theta_s的值:’);
theta_T1=input(‘请输入theta_T1的值:’); %低频移相线长度
theta_T2=input(‘请输入theta_T2的值:’); %高频移相线长度
f1=input(‘请输入低频频率(单位GHz):’);
f2=input(‘请输入高频频率(单位GHz):’);
n=f2/f1;
ZT=50;
Zs=ZTabs(sind(theta_T1))/abs(sind(theta_s)) %在频率f1处
% 求解出Zs，Theta_s以后，就可以代入（6）求出K（f1）,K(f2)
K_f1=(cosd(theta_s)-cosd(theta_T1))/sind(theta_s); % @f1
K_f2=(cosd(ntheta_s)-cosd(theta_T2))/sind(n*theta_s); % @f2
% 求解完K以后就可以代入（5）中就可以求出相对应的直接BS
Bs_f1=K_f1/Zs % @f1 BS_f1可以正可以负
Bs_f2=K_f2/Zs % @f2 BS_f2可以正可以负

% 下面来正式求解Bs枝节的值，注意theta_oc长度为90度
Zc_1=50; %Zc_1可以随便取值
Zc_2=50; %Zc_2可以随便取值
Zc_oc=50;%开路线的阻抗
theta_c1_f1=atand(-1/(Zc_1Bs_f1)) %第一段线长度
Ya_f2=(1i/Zc_1)(Zc_1Bs_f2-tand(theta_c1_f1f2/f1))/(1+Zc_1Bs_f2tand(theta_c1_f1f2/f1));
Yc_f2=(1i/Zc_oc)tan(pi/2f2/f1);
Yb_f2=Ya_f2-Yc_f2;
theta_c2_f2_open=atand(Zc_2imag(Yb_f2)) % 对于开路线
theta_c2_f2_short=atand(-1/(Zc_2*imag(Yb_f2))) %对于短路线

运行仿真后：

四、与论文结果对比

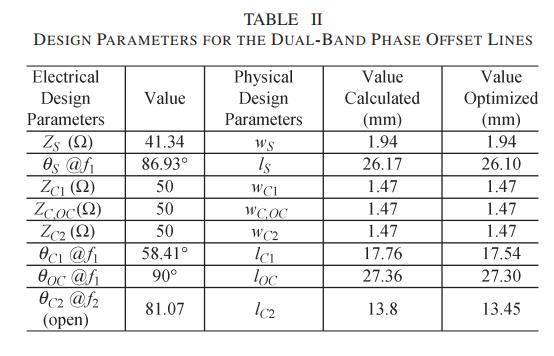
通过观察我们的结果和文章给出的Table 2进行对比，结果吻合，所以表明我们公式和软件算法都是正确的。

五、ADS软件仿真验证

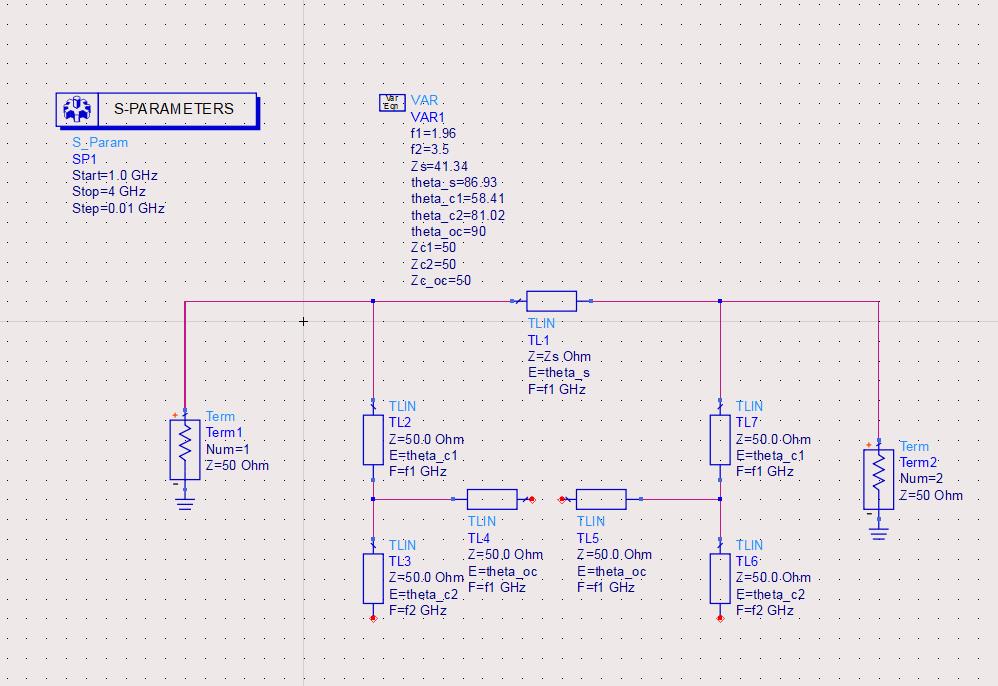
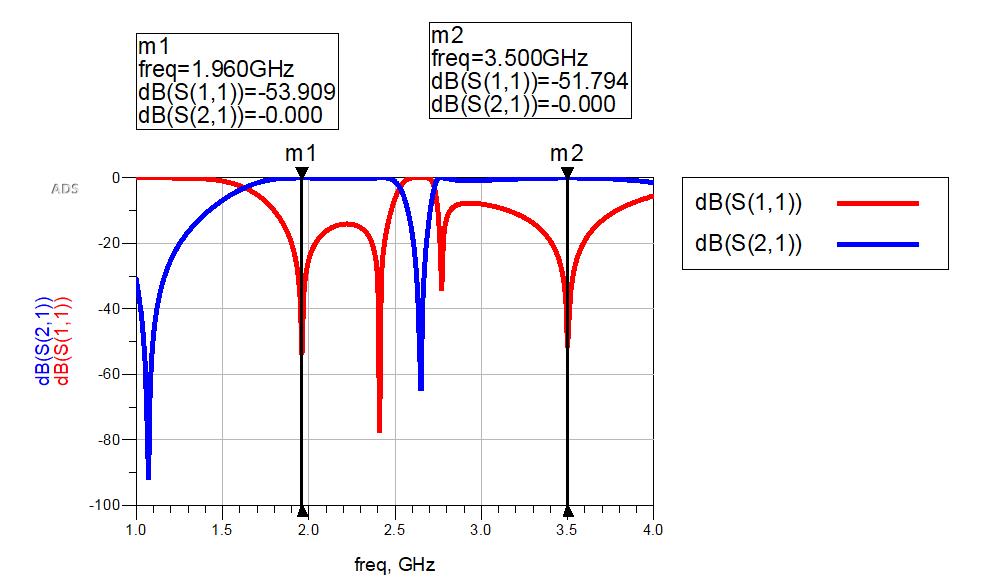
验证工程，结果正确。