Codeforces Global Round 16 A-E

Posted 2021-10-02 hesorchen

A. Median Maximization

n个非负数的和是s，问中位数最大可以是多少。

前一半都取0最优。

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

void solve()
{
    long long n, s;
    cin >> n >> s;
    long long m = (n + 1) / 2;
    n -= (m - 1);
    cout << (s / n) << endl;
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
        solve();
    return 0;
}

B. MIN-MEX Cut

给一个01字符串，一个01字符串的mex运算返回0/1/2。可以将所给的01字符串分割成若干个子字符串，问所有子字符串的mex总和最小是多少。

先将连续的相同字符都处理成一个字符。然后是一个01交替出现的字符串，考虑不分割时答案为2，所有1可以拆成单独的子字符串，贡献为0，连续的一段0可以拆成一个子字符串，贡献为1，也就是看连续的0出现了几段，和2取min即可。

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

void solve()
{
    string a;
    cin >> a;
    string b = a;
    a.clear();
    for (auto it : b)
    {
        if (a.size() && it == a.back())
            continue;
        a += it;
    }
    int s0 = 0;
    for (auto it : a)
        s0 += it == '0';
    cout << min(2, s0) << endl;
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
        solve();
    return 0;
}

C. MAX-MEX Cut

在B题的基础变为两个01字符串，分割的时候两个字符串同步。求所有子字符串最大mex和。

例如：

01100
11100

0 11 00
1 11 00

2 0  1

容易发现，除下列两种情况，其他都分割成长度为1的子字符串就是最优的。

01 
01

10
10

分类讨论太麻烦了，选择了DP，DP[i]只会从DP[i-1]、DP[i-2]转移

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

int dp[N];

int get(char a, char b)
{
    set<int> st;
    st.insert(a);
    st.insert(b);
    if (st.size() == 2)
        return 2;
    if (st.count('0'))
        return 1;
    return 0;
}
int get(char a, char b, char c, char d)
{
    set<int> st;
    st.insert(a);
    st.insert(b);
    st.insert(c);
    st.insert(d);
    if (st.size() == 2)
        return 2;
    if (st.count('0'))
        return 1;
    return 0;
}
void solve()
{
    int n;
    cin >> n;
    string a, b;
    cin >> a >> b;
    for (int i = 1; i <= n; i++)
        dp[i] = 0;
    a = ' ' + a;
    b = ' ' + b;
    dp[1] = get(a[1], b[1]);
    for (int i = 2; i <= n; i++)
    {
        dp[i] = max(dp[i], dp[i - 1] + get(a[i], b[i]));
        if (i >= 2)
            dp[i] = max(dp[i], dp[i - 2] + get(a[i], b[i], a[i - 1], b[i - 1]));
    }
    cout << dp[n] << endl;
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
        solve();
    return 0;
}

D1. Seating Arrangements (easy version)

读完题就会了。求顺序对即可（甚至不用数据结构优化）。

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

int a[N];
void solve()
{
    int n, m;
    cin >> n >> m;
    int ans = 0;
    for (int i = 1; i <= m; i++)
    {
        cin >> a[i];
        for (int j = 1; j < i; j++)
            ans += a[i] > a[j];
    }
    cout << ans << endl;
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
        solve();
    return 0;
}

D2. Seating Arrangements (hard version)

最后的结果是确定的，对于ai相同的，贪心从上到下，从右到左放置。

#include <bits/stdc++.h>
using namespace std;

const int N = 300 + 5;

int a[N * N];
int b[N * N];
int mp[N][N];
int fk[N][N];
void solve()
{
    int n, m;
    cin >> n >> m;
    int all = n * m;
    for (int i = 1; i <= all; i++)
    {
        cin >> a[i];
        b[i] = a[i];
    }
    sort(b + 1, b + 1 + all);
    int ct = 0;
    map<int, deque<int>> res;
    for (int i = 1; i <= all; i++)
        res[a[i]].push_back(i);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            mp[i][j] = b[++ct];

    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 1; j--)
        {
            fk[i][j] = res[mp[i][j]].front();
            res[mp[i][j]].pop_front();
        }

    int ans = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            for (int k = 1; k < j; k++)
                ans += fk[i][k] < fk[i][j];
    cout << ans << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

E. Buds Re-hanging

能切的先全部切出来。最后肯定形成了若干个深度为2、叶子数量大于0的子树。

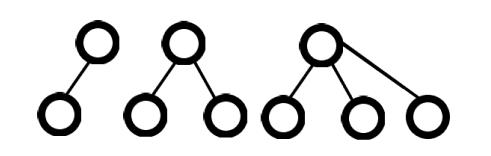
然后将所有子树连接起来即可。显然将当前子树的根连接到上一个子树的一个叶子上是最优的。因此答案就是拆完之后的叶子总数-（子树的数量-1）

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 5;

vector<int> mp[N];

int typ[N]; //1为叶子结点 0为切断后子树的根结点
int num[N]; //typ[2]的根结点含有的儿子数量

int dfs(int u, int fa)
{
    vector<int> vec;
    for (auto v : mp[u])
    {
        if (v == fa)
            continue;
        vec.emplace_back(dfs(v, u));
    }
    int num_leaves = 0;
    for (auto it : vec)
        num_leaves += it;
    if (num_leaves) //儿子节点有叶子 就可以切断
    {
        typ[u] = 0;
        num[u] = num_leaves;
    }
    else
        typ[u] = 1; //叶子返回1
    return typ[u];
}
void solve()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        mp[i].clear();
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        mp[u].emplace_back(v);
        mp[v].emplace_back(u);
    }
    dfs(1, -1);

    int res = 0, ans = 0;
    for (int i = 1; i <= n; i++)
        if (typ[i] == 0) //i是一颗子树的根
        {
            ans += num[i]; //叶子总数
            res++;         //子树的数量
        }

    cout << ans - (res - 1) << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}