动态规划解最长公共子串

Posted 2021-10-02 数据结构和算法

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

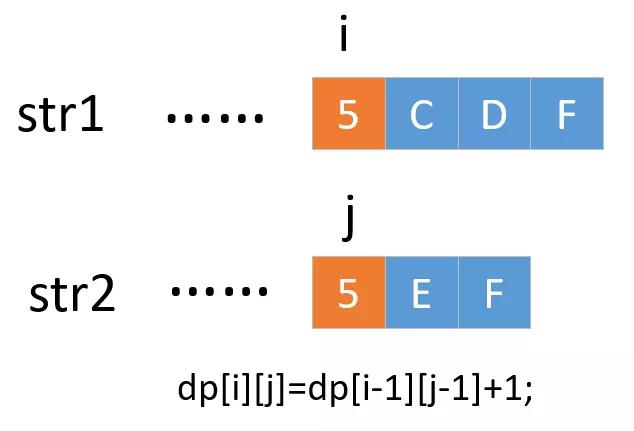
有了递推公式，代码就比较简单了，我们使用两个变量，一个记录最长的公共子串，一个记录最长公共子串的结束位置，最后再对字符串进行截取即可，来看下代码

public String LCS(String str1, String str2) {
    int maxLenth = 0;//记录最长公共子串的长度
    //记录最长公共子串最后一个元素在字符串str1中的位置
    int maxLastIndex = 0;
    int[][] dp = new int[str1.length() + 1][str2.length() + 1];
    for (int i = 0; i < str1.length(); i++) {
        for (int j = 0; j < str2.length(); j++) {
            //递推公式，两个字符相等的情况
            if (str1.charAt(i) == str2.charAt(j)) {
                dp[i + 1][j + 1] = dp[i][j] + 1;
                //如果遇到了更长的子串，要更新，记录最长子串的长度，
                //以及最长子串最后一个元素的位置
                if (dp[i + 1][j + 1] > maxLenth) {
                    maxLenth = dp[i + 1][j+1];
                    maxLastIndex = i;
                }
            } else {
                //递推公式，两个字符不相等的情况
                dp[i + 1][j+1] = 0;
            }
        }
    }
    //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置
    return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);
}

时间复杂度：O（m*n），m和n分别表示两个字符串的长度

空间复杂度：O（m*n）

代码优化，把二维数组变为一维数组

public String LCS(String str1, String str2) {
    int maxLenth = 0;//记录最长公共子串的长度
    //记录最长公共子串最后一个元素在字符串str1中的位置
    int maxLastIndex = 0;
    int[] dp = new int[str2.length() + 1];
    for (int i = 0; i < str1.length(); i++) {
        //注意这里是倒叙
        for (int j = str2.length() - 1; j >= 0; j--) {
            //递推公式，两个字符相等的情况
            if (str1.charAt(i) == str2.charAt(j)) {
                dp[j + 1] = dp[j] + 1;
                //如果遇到了更长的子串，要更新，记录最长子串的长度，
                //以及最长子串最后一个元素的位置
                if (dp[j + 1] > maxLenth) {
                    maxLenth = dp[j + 1];
                    maxLastIndex = i;
                }
            } else {
                //递推公式，两个字符不相等的情况
                dp[j + 1] = 0;
            }
        }
    }
    //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置
    return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);
}

时间复杂度：O（m*n），m和n分别表示两个字符串的长度
空间复杂度：O（n），只需要一个一维数组即可

总结

这题比较简单，很久以前也讲过这题370，最长公共子串和子序列，之前只是返回一个具体的数字即可，而这题需要返回具体的公共子串，多了一步。