Naive Operations （线段树 分析复杂度）

Posted 2021-09-29 昵称很长很长真是太好了

题目：
给出一个长度为n初值为0的数组，以及长度为n的b数组，然后q次操作，add(l,r) 使得区间l-r所有元素+1，或者查询l~r区间a[i]/b[i]的和
题解：
很少情况下能很快写出一道线段树题目，关键还0调试
首先题目说了b是个排列，突破点也就是b这个条件。
因为题目是向下取整，那么假设b[1]=100000,那么你对他修改99999次都是没有任何影响的，那岂不是可以不去修改这个点。同理考虑其他的节点，发现b[i]越大，那么a[i]/b[j]如果变大的话，需要修改的次数也会越多。
我们计算一下这个次数
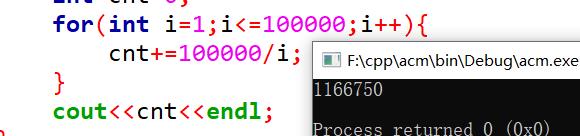级别是一个1e6的级别，nlogn可以过。

那么我们用一个$imi{n}_i$表示你还需要对$a_i$加几次，才会使得$a_i/b_i$增大1.
如果imin用最小值去维护区间，每次区间加的时候如果发现区间最小值为1，那么递归下去修改贡献，否则直接懒标记把区间最小值-1。

代码：

#include<bits/stdc++.h>
using namespace std;
#define endl '\\n'
#define int long long
const int maxn = 1e5 + 10;
const int mod=998244353;

int b[maxn];
int imin[maxn<<2],sum[maxn<<2],lazy[maxn<<2];

void push_up(int node){
    imin[node]=min(imin[node<<1],imin[node<<1|1]);
    sum[node]=sum[node<<1]+sum[node<<1|1];
}

void build(int node,int start,int ends){
    lazy[node]=0;
    if(start==ends){
        sum[node]=0;
        imin[node]=b[start];
        return ;
    }
    int mid=(start+ends)>>1;
    build(node<<1,start,mid);
    build(node<<1|1,mid+1,ends);
    push_up(node);
}

void push_down(int node){
    if(lazy[node]){
        lazy[node<<1]+=lazy[node];
        lazy[node<<1|1]+=lazy[node];
        imin[node<<1]-=lazy[node];
        imin[node<<1|1]-=lazy[node];
    }
    lazy[node]=0;
}

void update(int node,int start,int ends,int l,int r){
    if(start==ends){
        if(imin[node]==1){
            imin[node]=b[start];
            sum[node]++;
        }
        else imin[node]--;
        return ;
    }
    if(l<=start&&ends<=r&&imin[node]!=1){
        lazy[node]+=1;
        imin[node]--;
        return ;
    }
    push_down(node);
    int mid=start+ends>>1;
    if(l<=mid) update(node<<1,start,mid,l,r);
    if(mid<r) update(node<<1|1,mid+1,ends,l,r);
    push_up(node);
}

int query(int node,int start,int ends,int l,int r){
    if(l<=start&&ends<=r){
        return sum[node];
    }
    int mid=start+ends>>1;
    push_down(node);
    int res=0;
    if(l<=mid) res+=query(node<<1,start,mid,l,r);
    if(mid<r) res+=query(node<<1|1,mid+1,ends,l,r);
    return res;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n,q;

    while(cin>>n>>q){
        for(int i=1;i<=n;i++) cin>>b[i];
        build(1,1,n);
        while(q--){
            string s;
            cin>>s;
            if(s[0]=='a'){
                int x,y;
                cin>>x>>y;
                update(1,1,n,x,y);
            }
            else{
                int x,y;
                cin>>x>>y;
                int ans=query(1,1,n,x,y);
                cout<<ans<<endl;
            }
        }
    }

}