LeetCode通关:连刷三十九道二叉树,刷疯了!⭐四万字长文搞定二叉树,建议收藏!⭐
Posted 三分恶
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode通关:连刷三十九道二叉树,刷疯了!⭐四万字长文搞定二叉树,建议收藏!⭐相关的知识,希望对你有一定的参考价值。
分门别类刷算法,坚持,进步!
刷题路线参考:https://github.com/youngyangyang04/leetcode-master
大家好,我是拿输出博客来督促自己刷题的老三,这一节我们来刷二叉树,二叉树相关题目在面试里非常高频,而且在力扣里数量很多,足足有几百道,不要慌,我们一步步来。我的文章很长,你们 收藏一下。
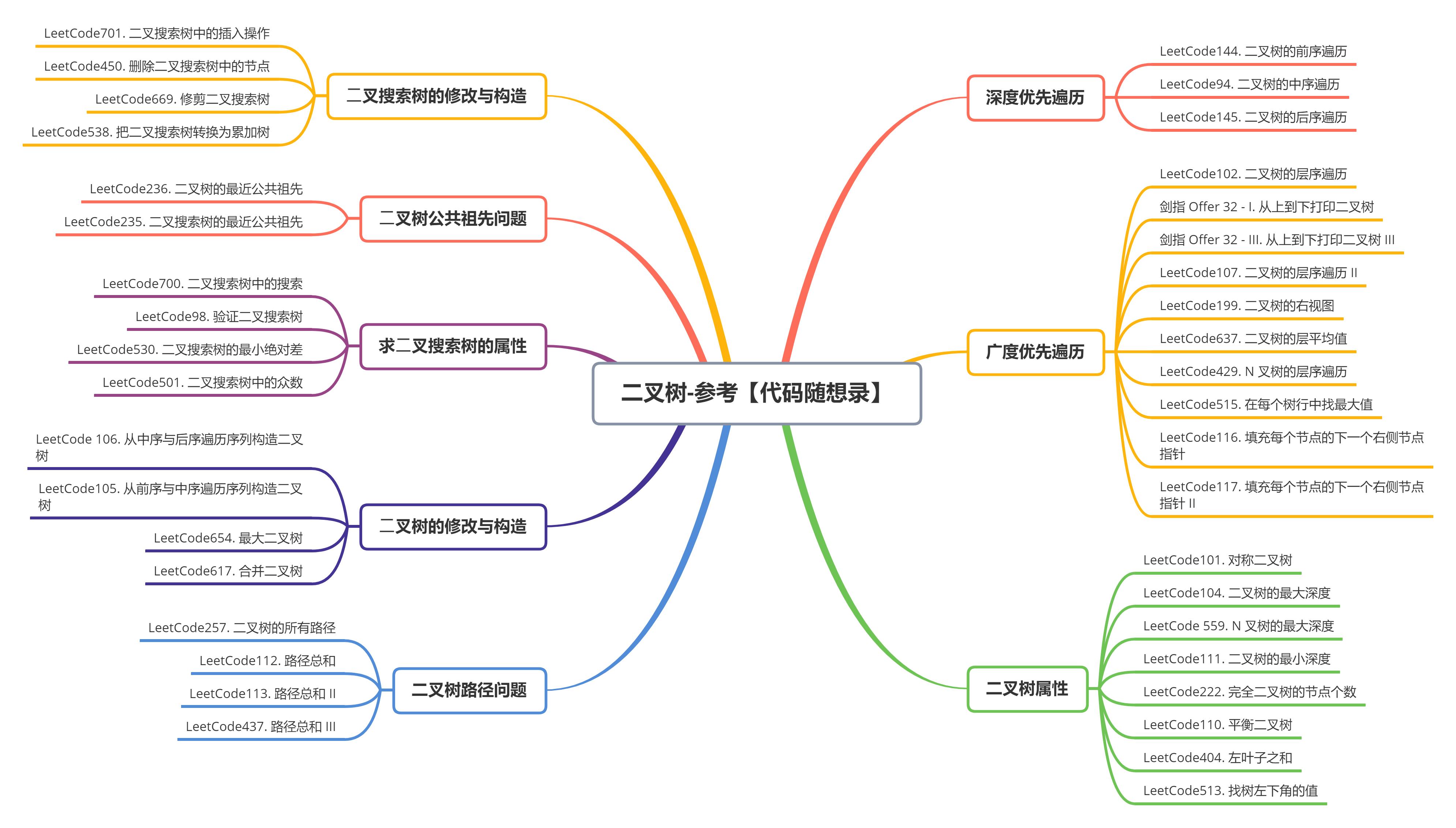
二叉树基础
二叉树是一种比较常见的数据结构,在开始刷二叉树之前,先简单了解一下一些二叉树的基础知识。更详细的数据结构知识建议学习《数据结构与算法》。
什么是二叉树
二叉树是每个节点至多有两棵子树的树。
二叉树主要的两种形式:满二叉树和完全二叉树。
-
满⼆叉树:如果⼀棵⼆叉树只有度为0的结点和度为2的结点,并且度为0的结点在同⼀层上,则这棵⼆
叉树为满⼆叉树。一棵深度为k的满二叉树节点个数为2k -1。
-
完全⼆叉树:至多只有最下面的两层结点的度数可以小于 2, 并且最下一层上的结点都集中在该层最左边的若干位置上, 则此二叉树称为完全二叉树。
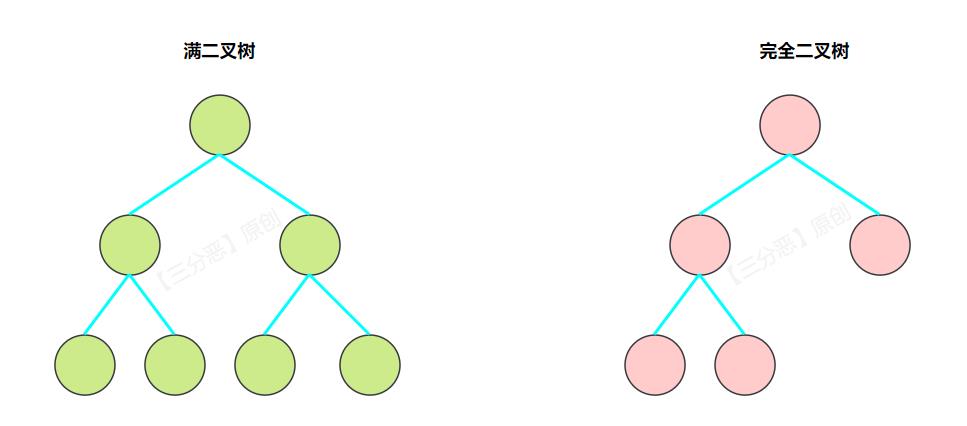
我们可以看出满二叉树是完全二叉树, 但完全二叉树不一定是满二叉树。
⼆叉搜索树
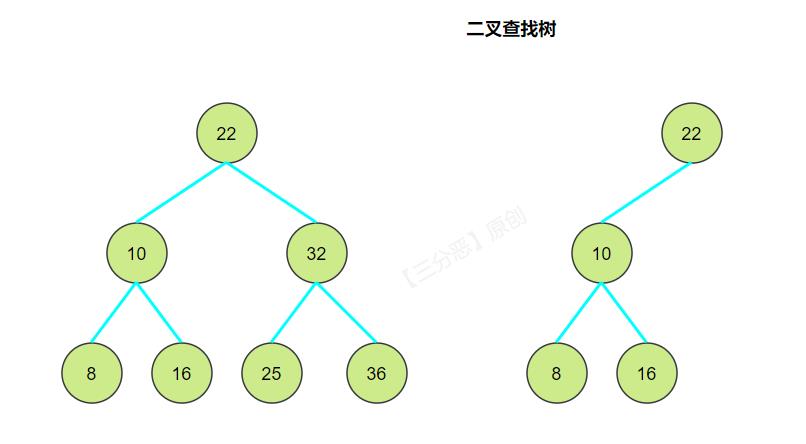
⼆叉搜索树,也可以叫二叉查找树、二叉排序树,是一种有序的二叉树。它遵循着左小右大的规则:
- 若它的左⼦树不空,则左⼦树上所有结点的值均⼩于它的根结点的值;
- 若它的右⼦树不空,则右⼦树上所有结点的值均⼤于它的根结点的值;
- 它的左、右⼦树也分别为⼆叉搜索树
二叉树存储结构
和线性表类似,二叉树的存储结构也可采用顺序存储和链式存储两种方式。
顺序存储是将二叉树所有元素编号,存入到一维数组的对应位置,比较适合存储满二叉树。

由于采用顺序存储结构存储一般二叉树造成大量存储空间的浪费, 因此, 一般二叉树的存储结构更多地采用链式的方式。
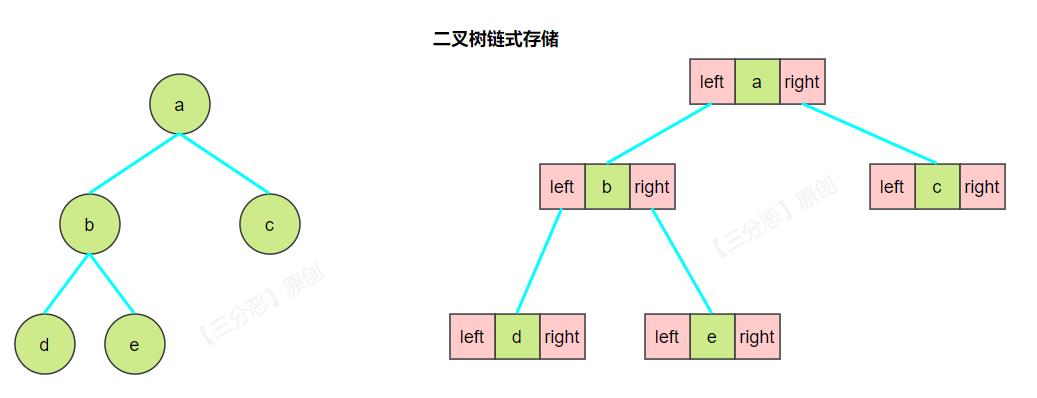
二叉树节点
我们在上面已经看了二叉树的链式存储,注意看,一个个节点是由三部分组成的,左孩子、数据、右孩子。
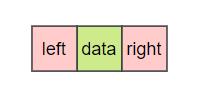
我们来定义一下二叉树的节点节点:
/**
* @Author: 三分恶
* @Date: 2021/6/8
* @Description:
**/
public class TreeNode {
int val; //值
TreeNode left; //左子树
TreeNode right; //右子树
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
二叉树遍历方式
⼆叉树主要有两种遍历⽅式:
-
深度优先遍历:先往深⾛,遇到叶⼦节点再往回⾛。
-
⼴度优先遍历:⼀层⼀层的去遍历。
那么从深度优先遍历和⼴度优先遍历进⼀步拓展,才有如下遍历⽅式:
-
深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
-
⼴度优先遍历
- 层次遍历(迭代法)
我们耳熟能详的就是根、左、右三种遍历,所谓根、左、右指的就是根节点的次序:
- 前序遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
还有一种更利于记忆的叫法:先根遍历、中根遍历、后根遍历,这种说法就更一目了然了。
我们来看一个图例:
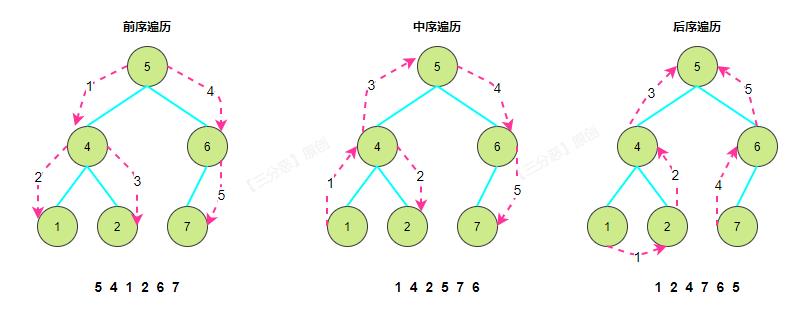
具体的算法实现主要有两种方式:
- 递归:树本身就是一种带着递归性质的数据结构,使用递归来实现深度优先遍历还是非常方便的。
- 迭代:迭代需要借助其它的数据结构,例如栈来实现。
好了,我们已经了解了二叉树的一些基础知识,接下来,面对LeetCode的疯狂打击吧!

深度优先遍历基础
递归基础
二叉树是一种天然递归的数据结构,我们先简单碰一碰递归。

递归有三大要素:
-
递归函数的参数和返回值
确定哪些参数是递归的过程中需要处理的,那么就在递归函数⾥加上这个参数, 并且还要明确每次递归的返回值是什么进⽽确定递归函数的返回类型。
-
终⽌条件:
递归需要注意终止条件,终⽌条件或者终⽌条件写的不对,操作系统的内存栈就会溢出。
-
单层递归的逻辑
确定单层递归的逻辑,在单层里会重复调用自己来实现递归的过程。
好了,那么我们开始吧!
LeetCode144. 二叉树的前序遍历
那么先从二叉树的前序遍历开始吧。
☕ 题目:LeetCode144. 二叉树的前序遍历 (https://leetcode-cn.com/problems/binary-tree-preorder-traversal/)
❓ 难度:简单
📕 描述:给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
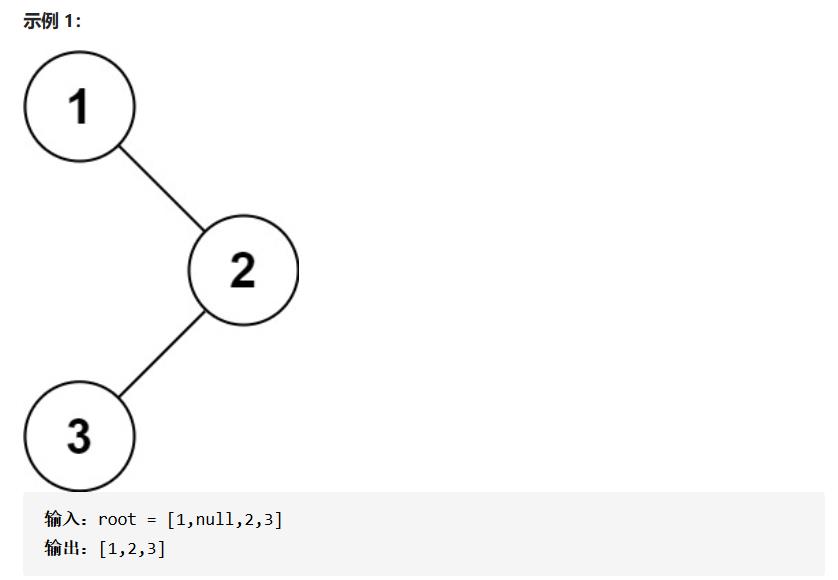
💡 思路:
递归法前序遍历
我们前面看了递归三要素,接下来我们开始用递归法来进行二叉树的前序遍历:
- 确定递归函数的参数和返回值:因为要打印出前序遍历节点的数值,所以参数⾥需要传⼊List用来存放节点的数值;要传入节点的值,自然也需要节点,那么递归函数的参数就确定了;因为节点数值已经存在List里了,所以递归函数返回类型是void,代码如下:
void preOrderRecu(TreeNode root, List<Integer> nodes)
- 确定终⽌条件:递归结束也很简单,如果当前遍历的这个节点是空,就直接return,代码如下:
//递归结束条件
if (root == null) {
return;
}
- 确定单层递归的逻辑:前序遍历是根左右的顺序,所以在单层递归的逻辑里,先取根节点的值,再递归左子树和右子树,代码如下:
//添加根节点
nodes.add(root.val);
//递归左子树
preOrderRecu(root.left, nodes);
//递归右子树
preOrderRecu(root.right, nodes);
我们看一下二叉树前序遍历的完整代码:
/**
* 二叉树前序遍历
*
* @param root
* @return
*/
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> nodes = new ArrayList<>(16);
preOrderRecu(root, nodes);
return nodes;
}
/**
* 二叉树递归前序遍历
*
* @param root
* @param nodes
*/
void preOrderRecu(TreeNode root, List<Integer> nodes) {
//递归结束条件
if (root == null) {
return;
}
//添加根节点
nodes.add(root.val);
//递归左子树
preOrderRecu(root.left, nodes);
//递归右子树
preOrderRecu(root.right, nodes);
}
单元测试:
@Test
public void preorderTraversal() {
LeetCode144 l = new LeetCode144();
//构造二叉树
TreeNode root = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
root.left = node1;
node1.right = node2;
//二叉树先序遍历
List<Integer> nodes = l.preorderTraversal(root);
nodes.stream().forEach(n -> {
System.out.print(n);
});
}
复杂度:
- 🚗 时间复杂度:O(n),其中 n 是二叉树的节点数。
递归法会者不难,难者不会。只要能理解,这个是不是很轻松?😂
我们接下来,搞一下稍微麻烦一点的迭代法。
迭代法前序遍历
迭代法的原理是引入新的数据结构,用来存储遍历的节点。
递归的过程是不断往左边走,当递归终止的时候,就添加节点。现在使用迭代,我们需要自己来用一个数据结构存储节点。
那么用什么数据结构比较合适呢?我们自然而然地想到——栈。
迭代法的核心是: 借助栈结构,模拟递归的过程,需要注意何时出栈入栈,何时访问结点。
前序遍历地顺序是根左右,先把根和左子树入栈,再将栈中的元素慢慢出栈,如果右子树不为空,就把右子树入栈。
ps:注意啊,我们的写法将存储元素进列表放在了栈操作前面,栈的作用主要用来找右子树。
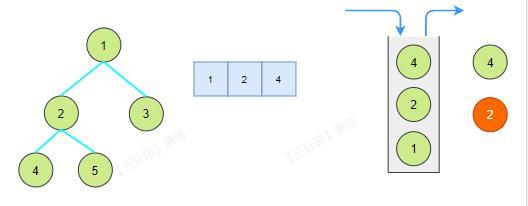
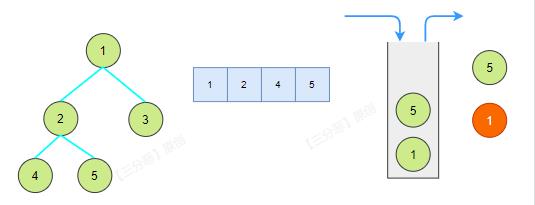
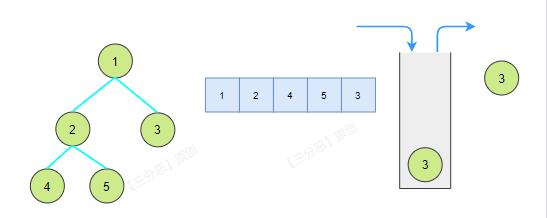
迭代和递归究其本质是一样的东西,不过递归里这个栈由虚拟机帮我们隐式地管理了。
/**
* 二叉树前序遍历-迭代法
*
* @param root
* @return
*/
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> nodes = new ArrayList<>(16);
if (root == null) {
return nodes;
}
//使用链表作为栈
Deque<TreeNode> stack = new LinkedList<TreeNode>();
while(root!=null || !stack.isEmpty()){
while(root!=null){
//根
nodes.add(root.val);
stack.push(root);
//左
root=root.left;
}
//出栈
root=stack.pop();
//右
root=root.right;
}
return nodes;
}
- 🚗时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
LeetCode94. 二叉树的中序遍历
☕ 题目:LeetCode94. 二叉树的中序遍历 (https://leetcode-cn.com/problems/binary-tree-inorder-traversal/)
❓ 难度:简单
📕 描述:给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
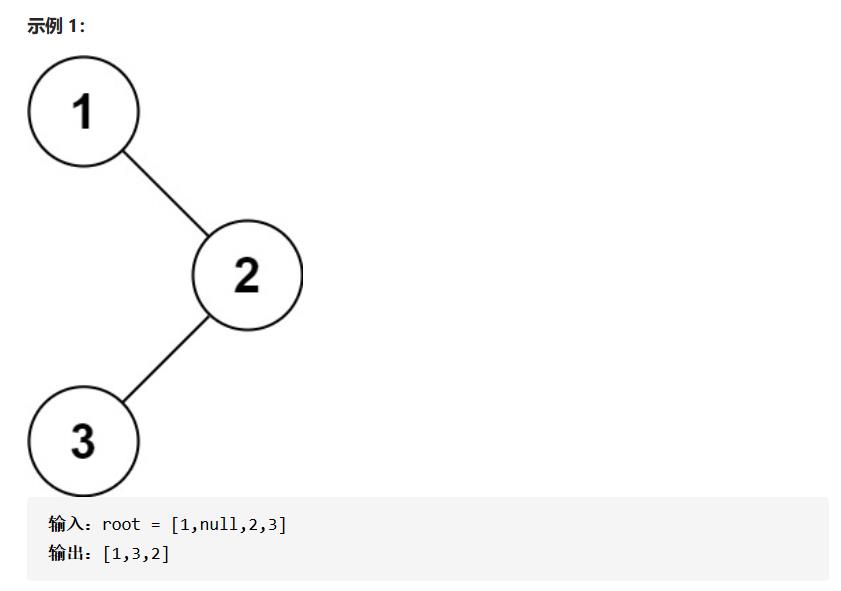
- 递归法中序遍历
我们在前面已经用递归法进行了二叉树大的前序遍历,中序遍历类似,只是把根节点的次序放到中间而已。
/**
* 中序遍历-递归
*
* @param root
* @param nodes
*/
void inOrderRecu(TreeNode root, List<Integer> nodes) {
if (root == null) {
return;
}
//递归左子树
inOrderRecu(root.left, nodes);
//根节点
nodes.add(root.val);
//递归右子树
inOrderRecu(root.right, nodes);
}
-
迭代法中序遍历
迭代法中序,也是使用栈来保存节点。
迭代法中序遍历和前序遍历类似,只是我们访问节点的时机不同而已:
- 前序遍历需要每次向左走之前就访问根结点
- 而中序遍历先压栈,在出栈的时候才访问

将节点的所有左孩子压入栈中,然后出栈,出栈的时候将节点的值放入List,如果节点右孩子不为空,就处理右孩子。
/**
* 中序遍历-迭代
*
* @param root
* @return
*/
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> nodes = new ArrayList<>(16);
if (root == null) {
return nodes;
}
//使用链表作为栈
Deque<TreeNode> stack = new LinkedList<TreeNode>();
while (root != null || !stack.isEmpty()) {
//遍历左子树
while (root != null) {
stack.push(root);
root = root.left;
}
//取出栈中的节点
root = stack.pop();
//添加取出的节点
nodes.add(root.val);
//右子树
root = root.right;
}
return nodes;
}
LeetCode145. 二叉树的后序遍历
☕ 题目:145. 二叉树的后序遍历 (https://leetcode-cn.com/problems/binary-tree-postorder-traversal/)
❓ 难度:简单
📕 描述:给定一个二叉树,返回它的 后序 遍历。

- 递归法后序遍历
递归法,只要理解了可以说so easy了!
/**
* 二叉树后序遍历-递归
*
* @param nodes
* @param root
*/
void postorderRecu(List<Integer> nodes, TreeNode root) {
if (root == null) {
return;
}
//递归左子树
postorderRecu(nodes, root.left);
//递归右子树
postorderRecu(nodes, root.right);
//根子树
nodes.add(root.val);
}
- 迭代法后序遍历
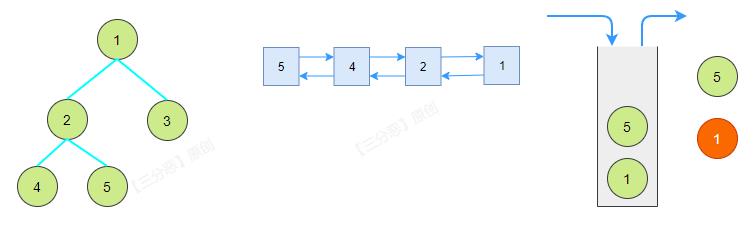
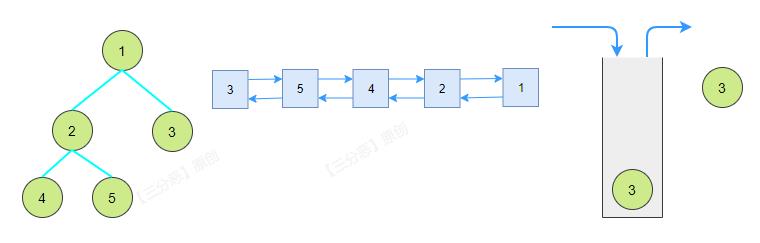
递归法后序遍历,可以用一个取巧的办法,套用一下前序遍历,前序遍历是根左右,后序遍历是左右根,我们只需要将前序遍历的结果反转一下,就是根左右。
如果使用Java实现,可以在链表上做文章,将尾插改成头插也是一样的效果。
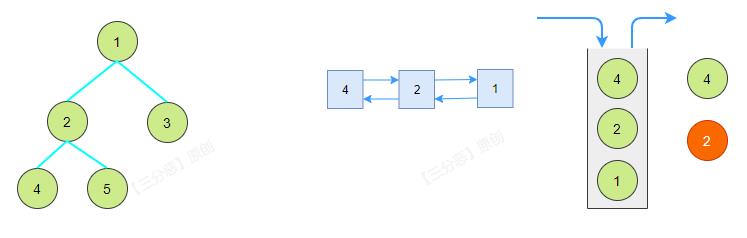
/**
* 二叉树后序遍历-迭代
*
* @param root
* @return
*/
public List<Integer> postorderTraversal(TreeNode root) {
//使用链表作为栈
Deque<TreeNode> stack = new LinkedList<TreeNode>();
//节点
LinkedList<Integer> nodes = new LinkedList<Integer>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
//头插法插入节点
nodes.addFirst(root.val);
//根节点入栈
stack.push(root);
//左子树
root = root.left;
}
//节点出栈
root = stack.pop();
//右子树
root = root.right;
}
return nodes;
}
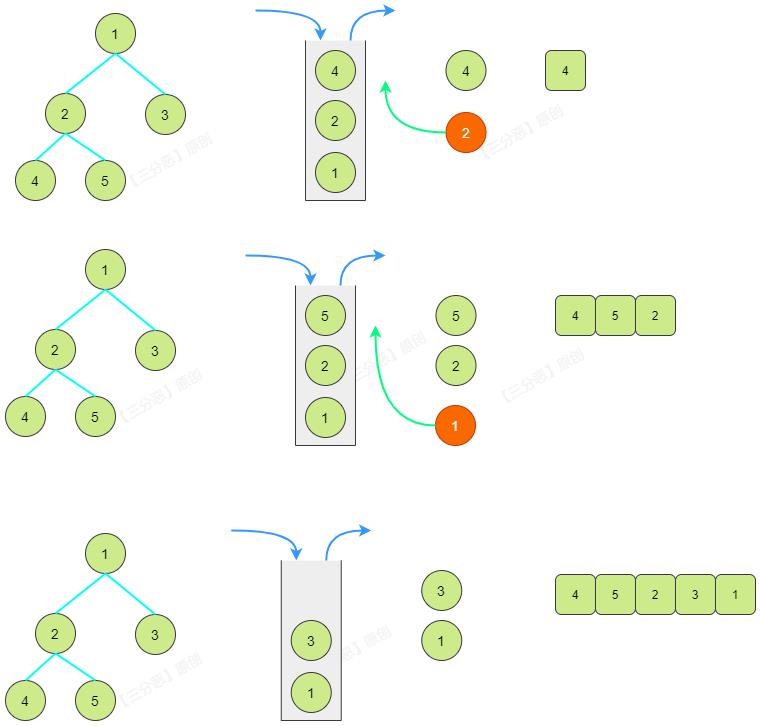
当然,这是一种取巧的做法,你说这不是真正的迭代法后序遍历,要真正的后序迭代二叉树,也不复杂,
重点在于:
- 如果右子树为空或者已经访问过了才访问根结点
- 否则,需要将该结点再次压回栈中,去访问其右子树
/**
* 二叉树后序遍历-迭代-常规
*
* @param root
* @return
*/
public List<Integer> postorderTraversal1(TreeNode root) {
//使用链表作为栈
Deque<TreeNode> stack = new LinkedList<TreeNode>();
//节点值存储
List<Integer> nodes = new ArrayList<>(16);
//用于记录前一个节点
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
//根节点入栈
stack.push(root);
//左子树
root = root.left;
}
//节点出栈
root = stack.pop();
//判断节点右子树是否为空或已经访问过
if (root.right == null || root.right == pre) {
//添加节点
nodes.add(root.val);
//更新访问过的节点
pre = root;
//使得下一次循环直接出栈下一个
root = null;
} else {
//再次入栈
stack.push(root);
//访问右子树
root = root.right;
}
}
return nodes;
}
广度优先遍历基础
LeetCode102. 二叉树的层序遍历
☕ 题目:102. 二叉树的层序遍历(https://leetcode-cn.com/problems/binary-tree-level-order-traversal/)
❓ 难度:中等
📕 描述:给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
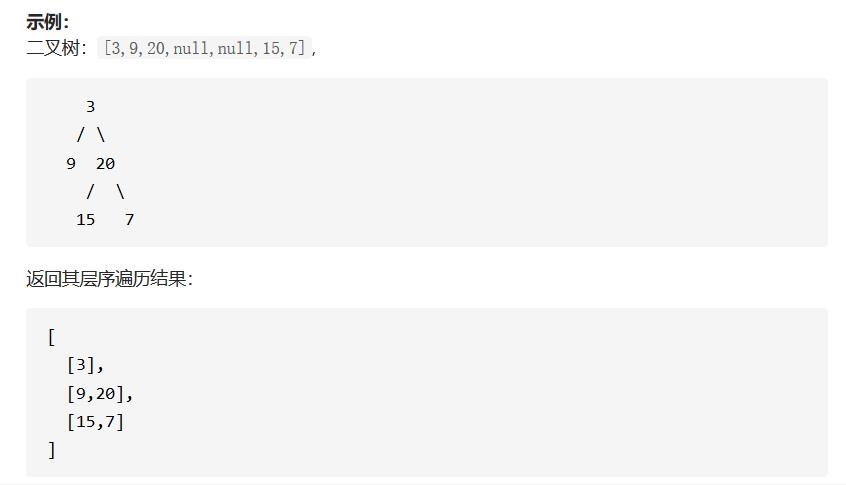
我们在前面已经使用迭代法完成了二叉树的深度优先遍历,现在我们来磕一下广度优先遍历。
在迭代法深度优先遍历里,我们用了栈这种数据结构来存储节点,那么层序遍历这种一层一层遍历的逻辑,适合什么数据结构呢?
答案是队列。
那么层序遍历的思路是什么呢?
使用队列,把每一层的节点存储进去,一层存储结束之后,我们把队列中的节点再取出来,左右孩子节点不为空,我们就把左右孩子节点放进去。
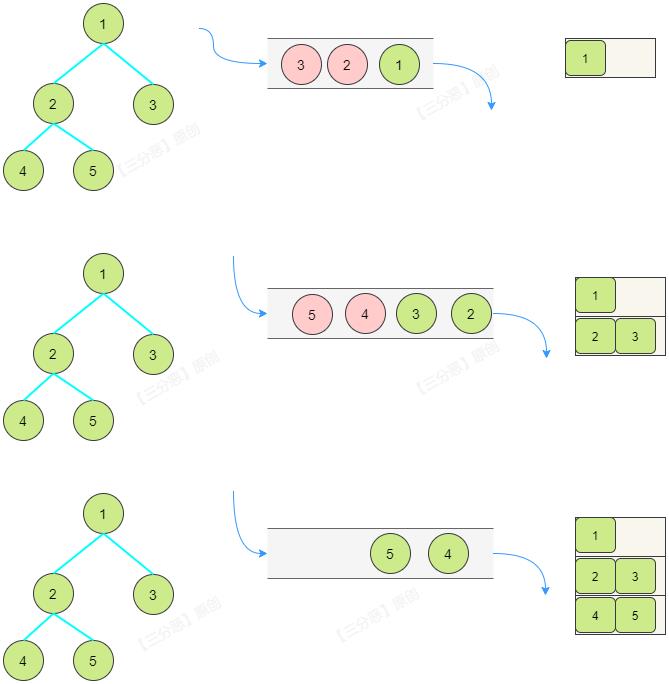
/**
* 二叉树层序遍历
*
* @param root
* @return
*/
public List<List<Integer>> levelOrder(TreeNode root) {
//结果集合
List<List<Integer>> result = new ArrayList<>(16);
if (root == null) {
return result;
}
//保存节点的队列
Queue<TreeNode> queue = new LinkedList<>();
//加入根节点
queue.offer(root);
while (!queue.isEmpty()) {
//存放每一层节点的集合
List<Integer> level = new ArrayList<>(8);
//这里每层队列的size要先取好,因为队列是不断变化的
int queueSize = queue.size();
//遍历队列
for (int i = 1; i <= queueSize; i++) {
//取出队列的节点
TreeNode node = queue.poll();
//每层集合中加入节点
level.add(node.val);
//如果当前节点左孩子不为空,左孩子入队
if (node.left != null) {
queue.offer(node.left);
}
//如果右孩子不为空,右孩子入队
if (node.right != null) {
queue.offer(node.right);
}
}
//结果结合加入每一层结果集合
result.add(level);
}
return result;
}
- 🚗时间复杂度:每个点进队出队各一次,故渐进时间复杂度为 O(n)。
好了,二叉树的深度优先遍历和广度优先遍历的基础已经完成了,接下来,我们看一看,在这两种遍历的基础上衍生出的各种变化吧!
广度优先遍历基础-变式
我们首先来看一下在层序遍历的基础上,稍微有一些变化的题目。
剑指 Offer 32 - I. 从上到下打印二叉树
☕ 题目:剑指 Offer 32 - I. 从上到下打印二叉树 (https://leetcode-cn.com/problems/cong-shang-dao-xia-da-yin-er-cha-shu-lcof/)
❓ 难度:中等
📕 描述:从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
💡思路:
这道题可以说变化非常小了。
该咋做?
就这么做!
/**
* 从上到下打印二叉树
*
* @param root
* @return
*/
public int[] levelOrder(TreeNode root) {
if (root == null) {
return new int[0];
}
List<Integer> nodes=new ArrayList<>(64);
//队列
Deque<TreeNode> queue = new LinkedList<>();
//根节点
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
nodes.add(node.val);
//左孩子入队
if (node.left != null) {
queue.offer(node