面试题 17.14. 最小K个数

Posted 2021-09-28 炫云云

面试题 17.14. 最小K个数

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

排序

对原数组从小到大排序后取出前 $k$ 个数即可。

class Solution:
    def smallestK(self, arr: List[int], k: int) -> List[int]:
        arr.sort()
        return arr[:k]

复杂度分析

• 时间复杂度： $O(n\log n)$, 其中 $n$ 是数组 arr 的长度。算法的时间复杂度即排序的时间复杂 度。
• 空间复杂度： $O(\log n)$, 排序所需额外的空间复杂度为 $O(\log n)$​ 。

大根堆

我们需要k个最小数，记录一个大小为k的大顶堆即可.首先将前 $k$ 个数插入大根堆中，随后从第 $k+1$ 个数开始遍历，如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。

而 Python 语言中的堆为小根堆，因此我们要对数组中所有的数取其相反数，才能使用小根堆维护前 $k$ 小值。

class Solution:
    def smallestK(self, arr: List[int], k: int) -> List[int]:
        ans = []
        for num in arr:
            heapq.heappush(ans, -num)
            if len(ans) > k:   # 大小为k的大根堆
                heapq.heappop(ans) # 删除最大的元素
        return [-num for num in ans]

• 时间复杂度：O $(n\log k)$, 其中 $n$ 是数组 $\mathrm{a}\mathrm{r}\mathrm{r}$ 的长度。由于大根堆实时维护前 $k$ 小值, 所以 插入删除都是 $O(\log k)$ 的时间复杂度，最坏情况下数组里 $n$ 个数都会插入，所以一共需要 $O(n\log k)$ 的时间复杂度。
• 空间复杂度：O $(k)$, 因为大根堆里最多 $k$​ 个数。

排序

本题使用排序算法解决最直观，对数组 arr 执行排序，再返回前 k 个元素即可。使用任意排序算法皆可，本文采用并介绍 快速排序 ，为下文 方法二 做铺垫。

快速排序原理：

• 快速排序算法有两个核心点，分别为 “哨兵划分” 和 “递归” 。
• 哨兵划分操作： 以数组某个元素（一般选取首元素）为 基准数 ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

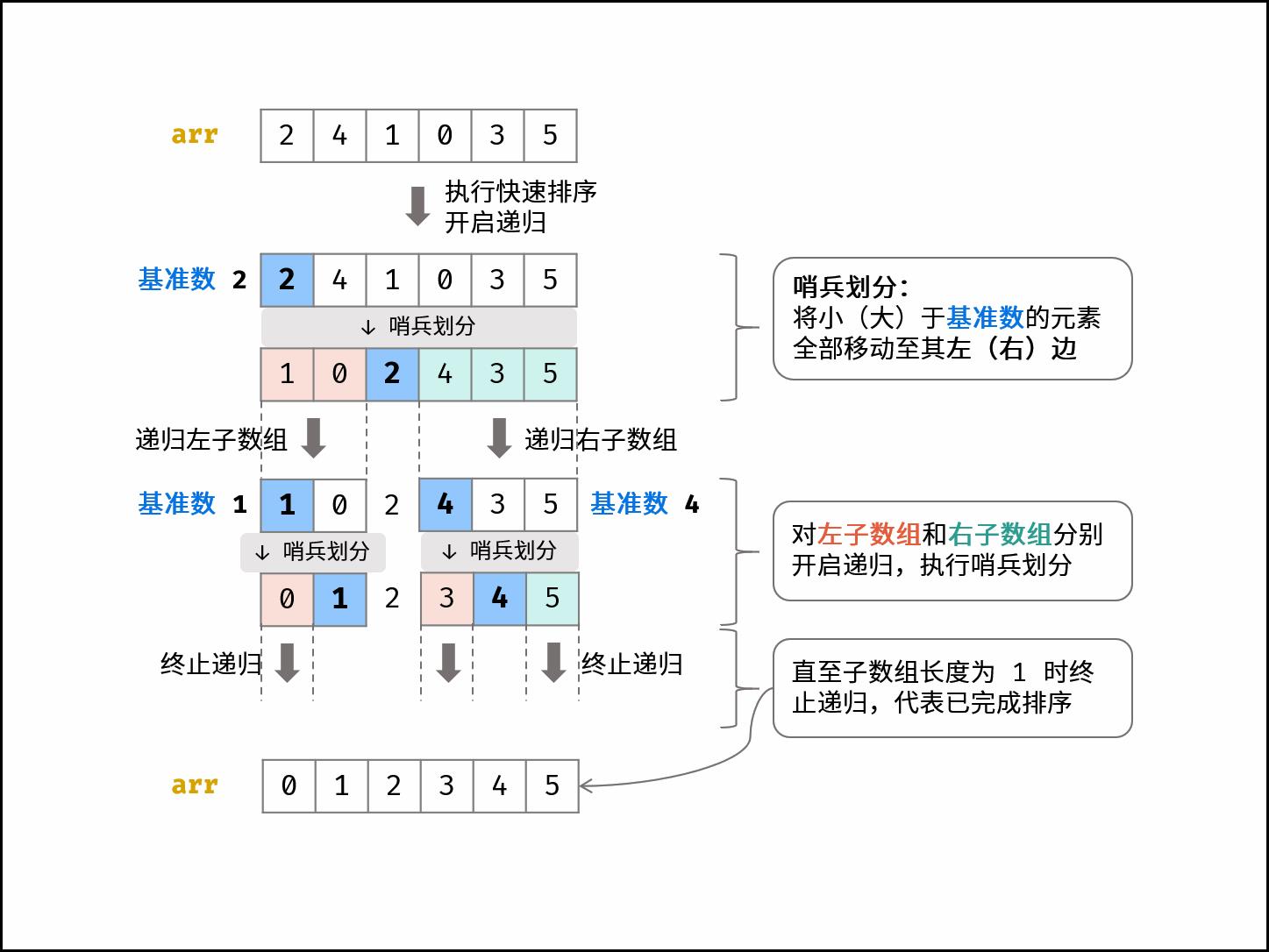
如下图所示，为哨兵划分操作流程。通过一轮 哨兵划分 ，可将数组排序问题拆分为 两个较短数组的排序问题 （本文称之为左（右）子数组）。

递归： 对 左子数组 和 右子数组 递归执行 哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

如下图所示，为示例数组 [2,4,1,0,3,5] 的快速排序流程。观察发现，快速排序和 二分法 的原理类似，都是以 $\log$ 时间复杂度实现搜索区间缩小。

class Solution(object):
    def getLeastNumbers(self, arr, k):
        """
        :type arr: List[int]
        :type k: int
        :rtype: List[int]
        """
        def quick_sort(arr, l, r):
            # 子数组长度为 1 时终止递归
            if l >= r: 
                return
            # 哨兵划分操作（以 arr[l] 作为基准数
            i, j = l, r
            while i < j:
                while i <j and arr[j] >= arr[l]:
                    j-=1
                while i <j and  arr[i] <= arr[l]:
                    i +=1
                arr[i], arr[j] = arr[j], arr[i] # arr[j] < arr[l] <arr[i]时候
            arr[l], arr[i] = arr[i], arr[l] # 交换哨兵
            # 递归左（右）子数组执行哨兵划分
            quick_sort(arr,l,i-1)
            quick_sort(arr,i+1,r)

        quick_sort(arr, 0, len(arr)-1)
        return arr[:k]
                

• 时间复杂度 $O(N\log N)$ ： 库函数、快排等排序算法的平均时间复杂度为 $O(N\log N)$ 。
• 空间复杂度 $O(N)$ ：快速排序的递归深度最好 (平均) 为 $O(\log N)$, 最差情况 (即输入数 组完全倒序 $)$ 为 $O(N)$​ 。

快速排序

快排的划分:小于等于分界值 pivot 的元素的都会被放到数组的左边，大于的都会被放到数组的右边，然后返回分界值的下标 left。

定义函数 select_k(nums,left,right) 表示划分数组 nums 的 [left,right] 部分，使前k 小的数在数组的左侧，调用快排的划分函数，假设划分函数返回的下标是 pos（表示分界值 pivot 最终在数组中的位置），即 pivot 是数组中第 pos 小的数，那么一共会有三种情况：

• 如果 pos == k-1，表示 pivot 就是第 k 小的数，直接返回即可；
• 如果 pos < k-1，表示第 k 小的数在 pivot 的右侧，因此递归调用select_k(nums,pos+1 ,right)；
• 如果 pos > k-1，表示第 k小的数在 pivot 的左侧，递归调用 select_k(nums,left ,pos-1)。

class Solution:
    def smallestK(self, nums: List[int], k: int) -> List[int]:
        
        def quick_sort(lists,left,right):
            if left >= right:
                return right
            # 选择参考点，该调整范围的第1个值
            pivot = lists[left]
            low = left  
            high = right
            while left < right:
                # 从右边开始查找大于参考点的值
                while left < right and lists[right] >= pivot:
                    right -= 1
                # 此时 lists[right] <pivot
                lists[left] = lists[right]  # 小于参考点的值先挪到左边 
                while left < right and  lists[left] <= pivot:
                    left += 1
                lists[right] = lists[left]  # 大于参考点的值值挪到右边
                
            # 写回改成的值
            lists[left] = pivot 
            return left 
    
        def select_k(nums,left,right):
            pos = quick_sort(nums,left,right)
            if pos == k-1:
                return #pos =index 
            elif  pos < k-1: # 在 pos 右侧
                select_k(nums,pos+1 ,right)
            else:                          # 在 pos 左侧
                select_k(nums,left ,pos-1) 

        select_k(nums,0, len(nums) - 1)
        return nums[:k]

#快速排序减治
class Solution:
    def smallestK(self, nums: List[int], k: int) -> List[int]:
        def select_k(l, r):
            if l >= r:
                return
            else:
                i = quick_sort(l, r)
                if i == k or i == k - 1:
                    return
                else:
                    if i < k - 1:
                        select_k(i + 1, r)
                    else:
                        select_k(l, i - 1)

        def quick_sort(l, r):
            pivot = nums[l] 
            j = l
            for i in range(l + 1, r + 1):
                if nums[i] < pivot:
                    j += 1
                    nums[i], nums[j] = nums[j], nums[i]
            nums[j], nums[l] = nums[l], nums[j]
            return j
        select_k(0, len(nums) - 1)
        return nums[:k]

基于快速排序的数组划分

题目只要求返回最小的 k 个数，对这 k 个数的顺序并没有要求。因此，只需要将数组划分为 最小的 k 个数 和 其他数字 两部分即可，而快速排序的哨兵划分可完成此目标。

根据快速排序原理，如果某次哨兵划分后 基准数正好是第 $k+1$​ 小的数字 ，那么此时基准数左边的所有数字便是题目所求的 最小的 $k$ 个数 。

根据此思路，考虑在每次哨兵划分后，判断基准数在数组中的索引是否等于 $k$ ，若 true 则直接返回此时数组的前 k 个数字即可。

算法流程：

getLeastNumbers() 函数：

1. 若 $k$ 大于数组长度，则直接返回整个数组；
2. 执行并返回 quick_sort() 即可；

quick_sort() 函数：

注意，此时 quick_sort() 的功能不是排序整个数组，而是搜索并返回最小的 $k$ 个数。

1. 哨兵划分：

• 划分完毕后，基准数为 arr[i] ，左 / 右子数组区间分别为 [l,i−1] , [i + 1, r] ；

2. 递归或返回：

• 若 $k<i$ ，代表第 $k+1$​ 小的数字在 左子数组 中，则递归左子数组；
• 若 $k>i$ ，代表第 $k+1$​小的数字在 右子数组 中，则递归右子数组；
• 若 $k=i$，代表此时 $arr[k]$ 即为第 $k+1$ 小的数字，则直接返回数组前 $k$ 个数字即可；

class Solution(object):
    def getLeastNumbers(self, arr, k):
        """
        :type arr: List[int]
        :type k: int
        :rtype: List[int]
        """
        if k >= len(arr): 
            return arr
        def quick_sort(l, r):
            i , j =l,r
            while i <j:
                while i <j and arr[j] >= arr[l]:
                    j-=1
                while i <j and  arr[i] <= arr[l]:
                    i +=1
                arr[i], arr[j] = arr[j], arr[i]
            arr[l], arr[i] = arr[i], arr[l]
            # i 为哨兵的索引
            if k < i: return quick_sort(l, i - 1) 
            if k > i: return quick_sort(i + 1, r)
            return arr[:k]
            
        return quick_sort(0, len(arr) - 1)

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)