516. 最长回文子序列

Posted 2021-09-28 炫云云

516. 最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

我们刚刚做过了 647.回文子串，求的是回文子串，而本题要求的是回文子序列， 要搞清楚这两者之间的区别。

回文子串是要连续的，回文子序列可不是连续的！

动态规划

第 1 步：定义状态

我们用 $dP(i,j)$ 表示字符串$s$在$[i,j]$范围内最长的回文子序列的长度为$dp[i][j]$。

第 2 步：思考状态转移方程

关键逻辑就是看s[i]与s[j]是否相同。

如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

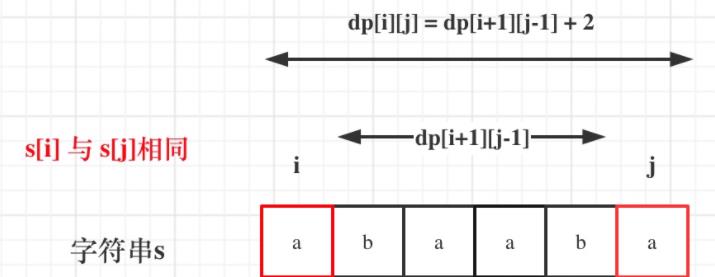
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为$dp[i+1][j]$。

加入s[i]的回文子序列长度为$dp[i][j-1]$。

即：$dp[i][j]=max(dp[i+1][j],dp[i][j-1])$;

if s[i] == s[j]:
    dp[i][j] = dp[i+1][j-1] + 2
else:
    dp[i][j] = max(dp[i+1][j], dp[i][j-1])

第 3 步：初始化

首先要考虑当 $i$ 和$j$ 相同的情况，从递推公式：$dp[i][j]=dp[i+1][j-1]+2$; 可以看出 递推公式是计算不到 $i$ 和$j$ 相同时候的情况。

所以需要手动初始化一下，当$i$与$j$相同，那么$dp[i][j]$一定是等于1的，即：一个字符的回文子序列长度就是1。其他情况$dp[i][j]$初始为0就行

第 4步：遍历顺序

从递推公式$dp[i][j]=dp[i+1][j-1]+2$ 和 $dp[i][j]=max(dp[i+1][j],dp[i][j-1])$ 可以看出，$dp[i][j]$是依赖于$dp[i+1][j-1]$ 和 $dp[i+1][j]$，如图：

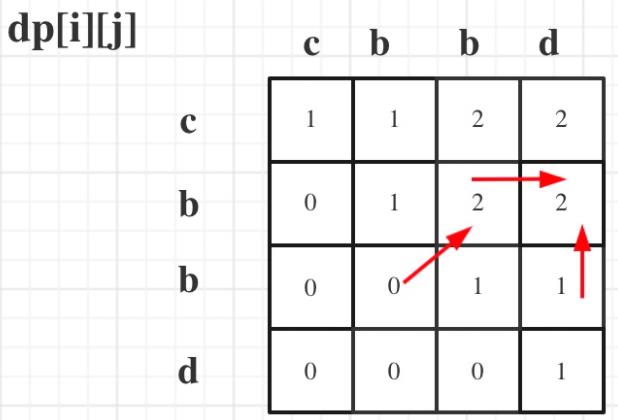
所以遍历i的时候一定要从下到上遍历，这样才能保证 dp[i][j]的计算。

输入s:“cbbd” 为例，dp数组状态如图：

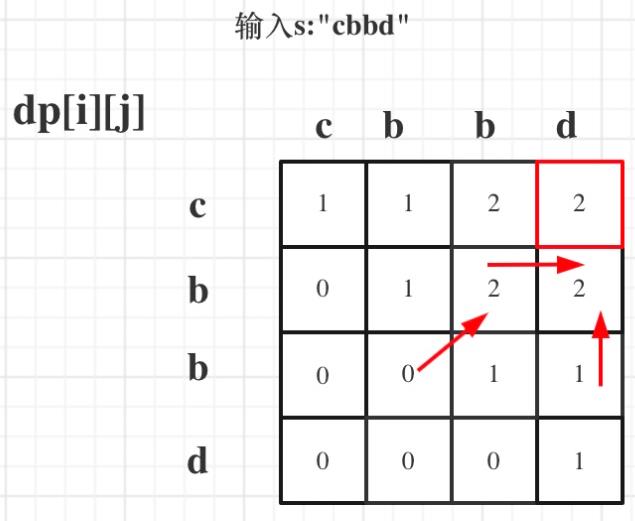
红色框即：$dp[0][-1]$; 为最终结果。

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        dp = [ [0] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = 1
        for i in range(n-1,-1,-1):# 自底向上
            for j in range(i+1,n):
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])
        return dp[0][-1]