300. 最长上升子序列

Posted 2021-09-28 炫云云

300. 最长上升子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列

示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。
说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

动态规划

题目的意思是让我们从给定数组中挑选若干数字，这些数字满足： 如果 i < j 则 nums[i] < nums[j]。问：一次可以挑选最多满足条件的数字是多少个。

这种子序列求极值的题目，应该要考虑到贪心或者动态规划。这道题贪心是不可以的，我们考虑动态规划。

按照动态规划定义状态的套路，我们有两种常见的定义状态的方式：

• $dp[i]$ : 以 $i$ 结尾（一定包括 i）所能形成的最长上升子序列长度, 答案是 $max(dp[i])$，其中 $i=0,1,2,...,n-1$
• $dp[i]$ : 以 $i$ 结尾（可能包括 $i$）所能形成的最长上升子序列长度，答案是 $dp[-1]$ （-1 表示最后一个元素）

容易看出第二种定义方式由于无需比较不同的 $dp[i]$ 就可以获得答案，因此更加方便。但是想了下，状态转移方程会很不好写，因为 $dp[i]$ 的末尾数字（最大的）可能是 任意 $j<i$ 的位置。

第一种定义方式虽然需要比较不同的 $dp[i]$ 从而获得结果，但是我们可以在循环的时候顺便得出，对复杂度不会有影响，只是代码多了一点而已。因此我们选择第一种建模方式。

由于 $dp[j]$ 中一定会包括 $j$，且以 $j$ 结尾， 那么 $nums[j]$ 一定是其所形成的序列中最大的元素，那么如果位于其后（意味着 $i>j$）的 $nums[i]>nums[j]$，那么 $nums[i]$ 一定能够融入 $dp[j]$ 从而形成更大的序列，这个序列的长度是 $dp[j]+1$。因此状态转移方程就有了：dp[i] = dp[j] + 1 (其中 i > j, nums[i] > nums[j])

以 [10, 9, 2, 5, 3, 7, 101, 18] 为例，当我们计算到 $dp[5]$的时候，我们需要往回和 0，1，2，3，4 进行比较。

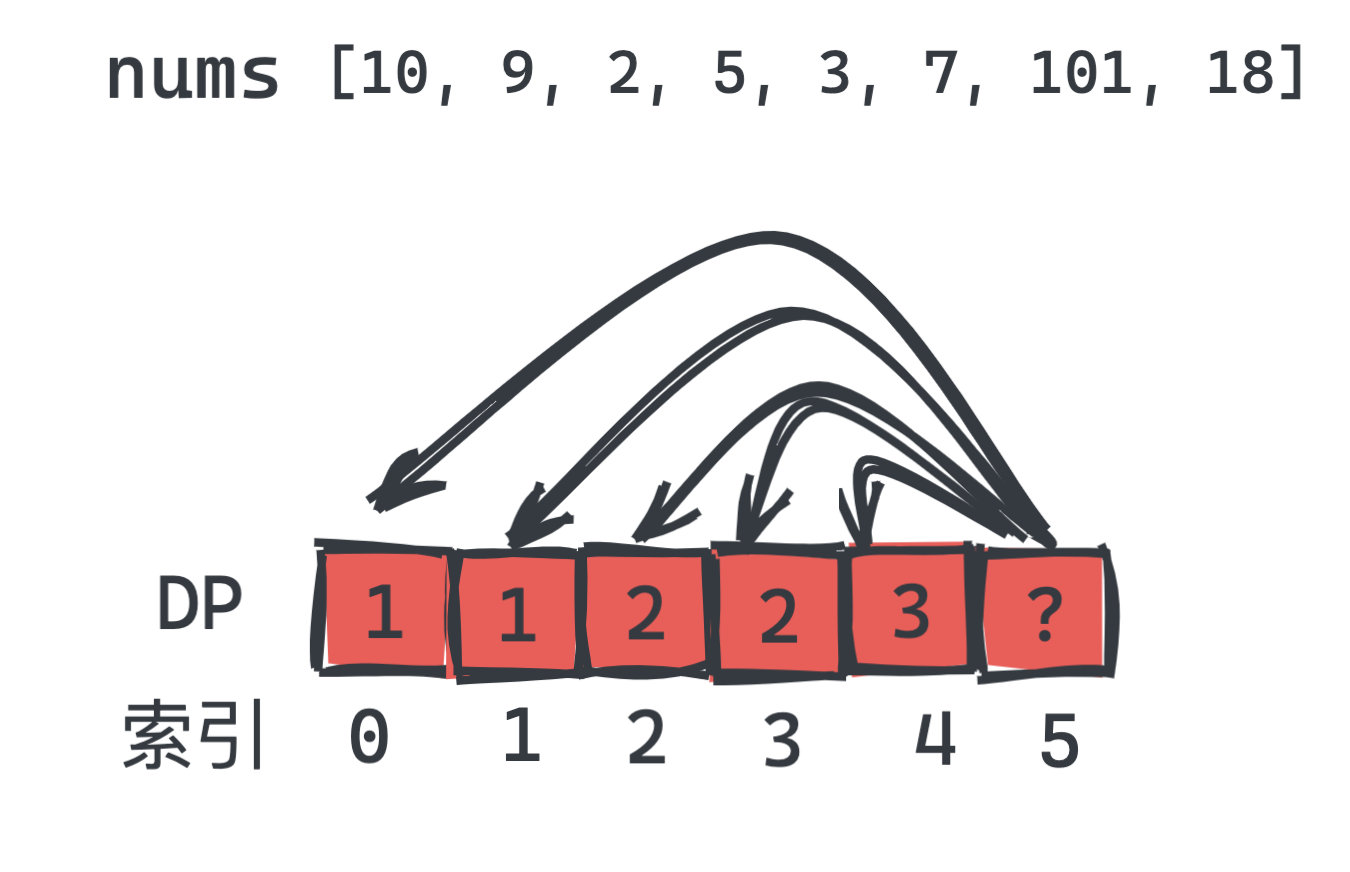
具体的比较内容是：

最后从三个中选一个最大的 **+ 1 赋给 dp[5]**即可。

复杂度分析

• 时间复杂度：$O(N^2)$
• 空间复杂度：$O(N)$

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 0: return 0
        dp = [1] * n
        ans = 1
        for i in range(n):
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
                    ans = max(ans, dp[i])
        return  ans

贪心 + 二分查找

考虑一个简单的贪心，如果我们要使上升子序列尽可能的长，则我们需要让序列上升得尽可能慢，因此我们希望每次在上升子序列最后加上的那个数尽可能的小。

基于上面的贪心思路，我们维护一个数组 $d[i]$​​, 表示长度为 $i+1$​​ 的最长上升子序列的末尾元素的最小值, 用 $len$​​ 记录目前最长上升子序列的长度, 起始时 len 为 $1,d[0]=nums[0]$​​ 。

同时我们可以注意到 $d[i]$ 是关于 $i$ 单调递增的。

我们依次遍历数组 $nums$​​​​ 中的每个元素，并更新数组 $d$​​​​ 和 $len$​​​​ 的值。

• 如果 $nums[i]>d[len-1]$ 则更新 len $=len+1$​, d.append(nums_i)
• 否则在 $d[0\dots len-1]$​​​​​​​​​ 中找满足 $nums[i]<d[k]$​​​​​​​​​ 的下标 $k$​​​​​​​​​, 并更新 $d[k]=$​​​​​​​​​ nums $[i{]}_{\text{。 }}$​​​​​​​​​ :

根据 $d$​​ 数组的单调性，我们可以使用二分查找寻找下标 $k$​​​​, 优化时间复杂度。 最后整个算法流程为：

• 设当前已求出的最长上升子序列的长度为 $len$​ (初始时为 1 ) , 从前往后遍历数组 nums, 在遍历到 $nums[i]$​ 时：
• 如果 $nums[i]>d[len-1]$​, 则直接加入到 $d$​ 数组末尾，并更新 len $=len+1$​;
• 否则，在 $d$​ 数组中二分查找，找到第一个比 nums $[i]$​ 大的数 $d[k]$​, 并更新 $d[k]=$​ nums $[i{]}_{\text{。 }}$​

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        d = []
        for nums_i in nums:
            if not d or nums_i > d[-1]:
                d.append(nums_i)
            else:
                left ,right =0 , len(d)-1
                k = right
                while left <= right:
                    mid = left +( right-left) // 2
                    if d[mid] >= nums_i: # K 在[left ,mid-1 ]
                        k = mid
                        right = mid-1
                    else:
                        left = mid +1
                d[k] = nums_i
        return len(d)

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        d = []
        for nums_i in nums:
            if not d or nums_i > d[-1]:
                d.append(nums_i)
            else:
                left ,right =0 , len(d)-1
                while left <right:
                    mid = left +( right-left) // 2
                    if d[mid] >= nums_i: # K 在[left ,mid ]
                        right = mid
                    else:
                        left = mid +1
                d[left] = nums_i # k == left
        return len(d)

相关题目

倒卖战利品