智能视觉食用指南

Posted 2021-09-28 Debroon

智能视觉食用指南

• • 卷积神经网络
  • • 卷积运算
    • 边缘检测
    • 填补 padding
    • 卷积步长
    • 3D卷积
    • 三类神经层
    • • 卷积层
      • 池化层
      • 全连接层
  • 深度卷积网络
  • 目标检测
  • 人脸识别
  • 风格迁移

卷积神经网络

在《深度学习食用指南》里，我们做了一个神经网络，在理论上，这个方法可以用来学习识别一切图像。

你只要把一张张的图片喂给神经网络，告诉它图上有什么，它终将自己发现各个东西的像素规律……但是在实践上，这个方法非常不可行。

比如在《深度学习食用指南》里，一张 64*64 的彩色图片就要用 1 万个数来描述，如果想让反向传播神经网络识别这样的图，那第一层每一个神经元都得有 1 万个权重w。

神经网络中的参数越多，所需要的训练素材就越多，否则就会过拟合。并不是任何照片都能用作训练素材，你必须事先靠人工标记照片上都有什么东西作为标准答案，才能给神经网络提供有效反馈。这么多训练素材上哪找呢？

即使你有海量的数据，可同时计算海量的参数，对算力的要求也非常高。

后来有人提出了卷积神经网络，其实就是借鉴人识别物品的方法。

人脑并不是每次都把一张图中所有的像素都放在一起考虑。

我们是：

• 看什么：让你找猫，你会先大概想象一下猫是什么样子，当你想象猫的时候，虽然不能完全说清，但你毕竟还是按照一定的规律去找。比如猫身上有毛，它有两个眼睛和一条尾巴，等等。

• 往哪看：也许猫在一个角落里，那你只要一个角落一个角落找就行，你没必要同时考虑图片的左上角和右下角。

总之，你看的不是单个的像素点，你看的是一片一片的像素群的模式变化。

实现这个思想，只是在最基本的像素到最终识别的物体之间加入了几个逻辑层 —— 也就是 “卷积层”。

“卷积” 是一种数学操作，可以理解成 “过滤”，或者叫 “滤波”，意思是从细致的信号中识别尺度更大一点的结构。

每一个卷积层识别一种特定规模的图形模式，后面一层只要在前面一层的基础上进行识别，这就解决了 “看什么” 和 “往哪看” 的问题。

第一层，是先从像素点中识别一些小尺度的线条结构，像垂直条纹、水平条纹、斑点、颜色从亮到暗等等各种小结构。

第二层，是根据第一层识别出来的小尺度结构识别像眼睛、耳朵、嘴之类的局部器官。

第三层，才是根据这些局部器官识别人脸。

其中每一层的神经网络从前面一层获得输入，经过深度学习之后再输出到后面一层，从小结构上看出更大、更复杂也更多的结构来，点 -> 线 -> 面。
 

---

卷积运算

矩阵卷积(二维)：矩阵$B$ 以某个步长在 矩阵$A$ 表面 滑动加权求和。

演示一下卷积过程，

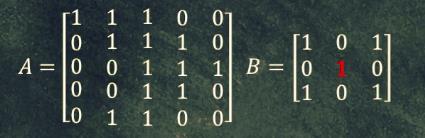
接着矩阵 $B$ 从矩阵 $A$ 的 左上角 准备滑动，如下图：

黄色区域的元素相乘，得到 $4$ 个 $1$，相加值为 $4$。

假设设定的滑动步长为 $1$ ，开始滑动，新一轮计算，方法相同，如下图：

继续滑动，对应位置相乘再求和得到 $4$，如下图：

继续滑动，对应位置相乘再求和得到 2，如下图：

…，最终矩阵卷积生成的矩阵，对比 矩阵$A$ 生成的矩阵小了一圈，如下图：

矩阵$B$ (小矩阵)，也被称为“卷积核”、“滤波器”；矩阵卷积（内积）也是卷积神经网络的原理。

• 结果矩阵维度：图像矩阵维度$(n,n)$，过滤器维度$(f,f)$，那结果矩阵$(n-f+1,n-f+1)$ 。

 

---

边缘检测

如果检查的是垂直条纹，那滤波器如下：

sobel = np.array([[  1,  0,  -1 ],                        
                  [  2,  0,  -2 ],
                  [  1,  2,  -1 ]]) 

如果检查的是水平条纹，那滤波器如下：

sobel = np.array([[ -1, -2, -1 ],                        
                  [  0,  0,  0 ],
                  [  1,  2,  1 ]]) 

更好的是，通过训练神经网络来找到更好的滤波器：

sobel = np.array([[ w1, w2, w3 ],                        
                  [ w4, w5, w6 ],
                  [ w7, w8, w9 ]]) 

其实我们检测一张图片，除了垂直条纹、水平条纹，还有 55 度角边缘、70 度角边缘······

一个滤波器负责一个子任务，那识别起来就是要多个滤波器啦。

过滤器越多，学到的特征越多。因为每个过滤器是不同的，所以他们会学到不同的特征。

我们可让输入图像同时与多个滤波器进行卷积运算。

比如下图同时和俩个滤波器进行卷积运算。

输入图像与每个滤波器进行卷积运算，都会生成一个相同维度的矩阵，而后我们可以把这俩个矩阵合并成一个二维的矩阵。

• 多滤波器的结果矩阵维度：图像矩阵维度$(n,n)$，过滤器维度$(f,f)$，那结果矩阵$(n-f+1,n-f+1)\ast m$
   

---

填补 padding

不得不说，卷积运算有俩个特点：

• 原数据变小了，比如矩阵是 5x5，滤波器 3x3，一波卷积变成了 3x3，也就是说，一张图片突然缩小了 $\frac{2}{5}$，我们更想保护数据。
• 矩阵里越是外围的元素，使用次数就越小，越是靠近中心，使用次数就越多，我们需要均衡一下。

所以，在卷积运算之前我们会进行填补。在原数据的矩阵中的最边缘，再加一条边。

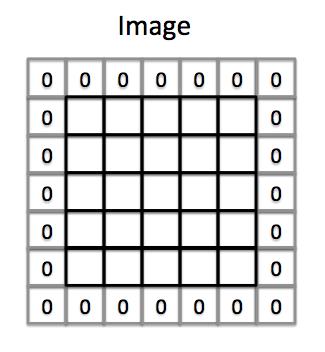
• padding 前的结果矩阵维度：图像矩阵维度$(n,n)$，过滤器维度$(f,f)$，那结果矩阵$(n-f+1,n-f+1)$ 。
• padding 后的结果矩阵维度：图像矩阵维度$(n,n)$，过滤器维度$(f,f)$，那结果矩阵$(n+2p-f+1,n+2p-f+1)$，因为我们只加了一条边，所以 $p=1$，这样卷积后原矩阵大小不变。

如果不用 padding 的话，图像周边的信息可能就会丢失了，原来边缘的元素，现在也可以参与运算多次了。
 

---

卷积步长

上面卷积运算中，滤波器在原数据矩阵中只移动了一个位置，这时卷积步长为 1，我们也可以设置为 2 啦（前后左右走 2 个位置）。

其实，卷积核的步长度代表提取的精度：

• 步长越大，提取特征越少；
• 反之，提取特征越多。

比如，大小为 3 的卷积核，如果步长为1，那相邻步之间就会有重复区域；如果步长为2，那么相邻步不会重复，也不会有覆盖不到的地方；如果步长为3，那么相邻步之间会有一道大小为1的缝隙，从某种程度来说，这样就遗漏了原图的信息，直观上理解是不好的。

• 卷积步长的结果矩阵维度：图像矩阵维度$(n,n)$，过滤器维度$(f,f)$，那结果矩阵$(\frac{n+2p-f}{s}+1,\frac{n+2p-f}{s}+1)$，$s$为步长。

 

---

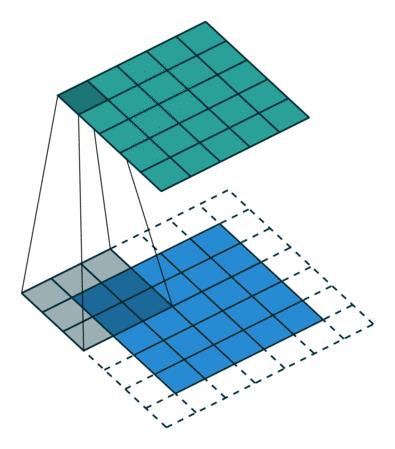
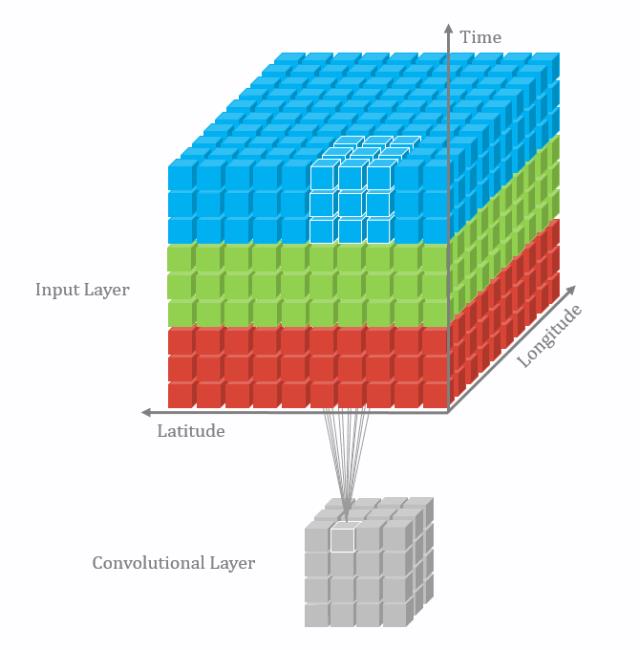
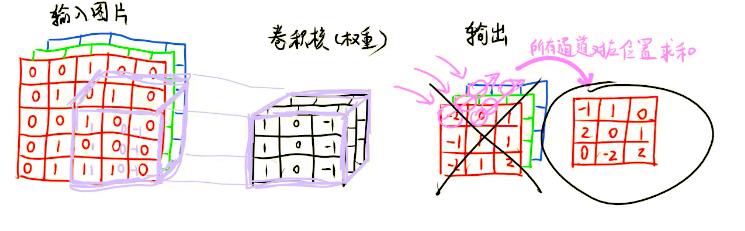
3D卷积

一张黑白的图片是二维，我们可以直接进行卷积运算，但一张彩色图片，要么先把彩色图片转为黑白图片（三维降到二维），要么把滤波器也上升到三维。

二维卷积：

三维卷积：

 

---

三类神经层

卷积层

前向传播计算：

• $z^{[1]}=w^{[1]}{a}^{[0]}+b^{[1]}$
• $a^{[1]}=f(z^{[1]})$

卷积层的前向传播计算：

如上图，卷积计算流程中加上阈值b和激活函数即可。

图中 6*6*3 的矩阵就是 $a_0$ (第 0 层)。

3*3*3 的过滤器就相当于 $w^{[1]}$。

俩者的 4*4 的矩阵加上b得到就是 $z^{[1]}$。

$z^{[1]}$ 经过了激活函数，得到的俩个 4*4 的矩阵会叠成一个 4*4*2 的矩阵，这就是 $a^{[1]}$。

这就是一个单独的卷积层：

• 输入 $a_0$：6*6*3
• 输出 $a^{[1]}$：4*4*2

单个卷积层再叠加成一个卷积神经网络。

 

---

池化层

池化层，可降低网络的计算量，提升稳定性。

 

---

全连接层

 

---

深度卷积网络

目标检测

人脸识别

风格迁移